基于潮流转移分布熵和负荷冲击灵敏度熵的电力系统关键线路识别
栗 然,靳保源
华北电力大学 电气与电子工程学院,河北 保定 071003)
0 引言
近年来,世界范围内的大停电事故频繁发生,造成了巨大的财产损失和严重的社会影响。相关研究发现,引发大停电事故的原因是输电设备过载或故障退出运行,引起系统发生连锁故障,而其中最主要的原因是线路潮流越限[1-2],因此,快速、准确地寻找对系统安全运行至关重要的关键线路并保证其稳定运行对可靠供电具有重要作用。
线路退出运行后,其承载的功率将会转移至其他线路,有可能造成其他线路过载,因此,了解各线路退出运行后的潮流转移情况对识别系统中的关键线路具有重要意义。在潮流转移区域搜索方面,文献[1]基于改进广度优先遍历方法提出了潮流转移区域确定方法;文献[2-3]采用图论相关知识得到断线线路的相关线路集合,进一步搜索潮流转移的范围;文献[4]则采用深度优先搜索方法搜索网络拓扑图中的割点及块来确定潮流转移区域;文献[5]基于割点和前k条最短路径的搜索方法提出了路径搜索方法。以上研究一方面所采用的搜索算法在大规模系统时实时性较差,另一方面基于图论方法而未结合基尔霍夫定律,所得结果需进一步验证。在潮流转移量计算方面,文献[6-7]通过模拟负荷增加,重新计算潮流得到各线路潮流增量,采用潮流熵来评判节点的脆弱性;文献[8]通过模拟支路断开计算系统潮流增量,并定义潮流转移熵来评估线路的脆弱性;文献[9]引入线路负载率对潮流转移熵进行改进,提高了电力系统的适用性。以上研究通过模拟某线路退出运行,得到目标线路在该线路断开后所增加的功率,但是在系统规模庞大的情况下,模拟量较大。文献[10]从直流潮流计算入手,假设转移功率与故障线路原始功率成比例,通过推导得到比例值,但由于直流潮流在形成节点导纳矩阵时不包含平衡节点的有关量,因此,采用该方法推导得到的结果无法得到与平衡节点相连线路的潮流转移量。
针对上述不足,本文依据直流潮流,采用谱分解得到电力系统的有效电阻矩阵,进而得到各线路断开后潮流转移区域的确定方法,以此为基础得到潮流增量计算方法,克服了传统方法采用搜索算法来搜索潮流转移区域及模拟线路断开重新计算潮流的不足,同时结合了基尔霍夫定律,更加符合实际电力系统。并对传统潮流转移熵进行改进,克服了传统潮流熵仅衡量潮流转移量在系统中分配的均匀程度而未考虑受转移线路容量裕度的不足,能够有效描述转移功率对线路容量裕度的使用情况。此外,定义了负荷冲击灵敏度熵来衡量各线路对系统负荷节点扰动的灵敏程度。最后,综合考虑潮流转移分布熵和负荷冲击灵敏度熵,采用IEEE 39节点系统算例进行仿真分析,验证了综合指标在电力系统关键线路识别中的有效性。
1 拉普拉斯矩阵和有效电阻矩阵
1.1 电力系统的拉普拉斯矩阵[11]
根据直流潮流得到节点i的注入功率为:
(1)
其中,Pi为节点i的注入功率;wij为节点i和j之间电抗的倒数;θi和θj分别为节点i和j的相角;N为系统中节点总数。
从而电力系统各节点注入功率计算公式如下:
(2)

(3)
(4)
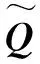
(5)
(6)

由拉普拉斯广义逆矩阵可得下式:
(7)

本文计算方法与传统直流潮流计算有些类似,但传统计算方法节点注入功率、相角及节点导纳矩阵中不含平衡节点的相关量。而由式(7)可知,采用本文计算方法计算平衡节点的相角并不一定为0,这是由于计算时已经选取0值作为参考点。
1.2 电力系统的有效电阻矩阵
引入拉普拉斯广义逆矩阵之后,支路i-j潮流表达式为:
θi-θj=rijPij
(8)
其中,Pij为支路i-j上的有功功率;rij为节点i与节点j之间的有效电阻。

(9)
其中,ei为第i个元素为1、其余元素为0的向量。
将式(9)等号右侧展开,得到下式:
(10)
则得到系统的有效电阻矩阵为[11]:
(11)
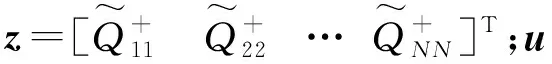
2 基于熵理论的关键线路评估模型
2.1 线路潮流转移分布熵
假设线路a-b断开,此时系统的网络拓扑结构发生变化,故拉普拉斯矩阵中与线路a-b相关的量也发生变化,但其他元素并不改变,即拉普拉斯矩阵受到影响的元素分别位于矩阵的a行、b行和a列、b列。线路a-b断开后,系统的拉普拉斯矩阵为[11]:
(13)


(14)
由修正矩阵的广义逆矩阵求法[12]可得:

(15)
直流潮流中,节点功率与支路功率存在关系:
(16)
其中,F为Nbr×1维线路潮流向量;Bb为Nbr×Nbr维支路导纳对角阵矩阵;R为Nbr×N维节点与支路的关联矩阵;Nbr为系统中线路总数。
可得到当线路a-b断开后,任意线路i-j上的转移功率可以由下式计算:
(17)
其中,Δfij为线路a-b断开后线路i-j上的转移功率;fab为线路a-b正常运行时的有功功率。
将式(15)代入式(17)中,则可得:
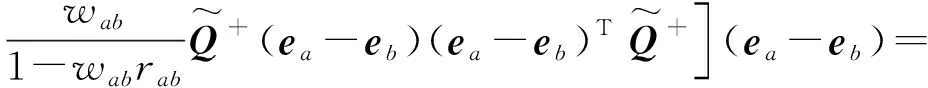
(18)
将式(10)代入式(18)中,则可得到线路i-j上的转移功率占断开线路a-b潮流的比例为:
(19)
但上式计算结果无法判别转移功率的大小,只能初步判断功率转移在其余线路的分配情况,即可确定潮流转移影响区域,因此,本文对上式进行修正:
(20)
其中,fb为基准功率,本文取为所有线路正常运行时有功功率之和。
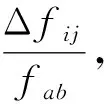

(21)
其中,sgn()为取符号函数。
系统中线路退出运行后会发生潮流转移,但并不是所有受影响的线路潮流都会增加,除了一部分线路潮流正向增加外,有些线路的潮流会降低,而有些线路则是反向增加。采用式(21)修正后,潮流是否会增加进一步分析如下:


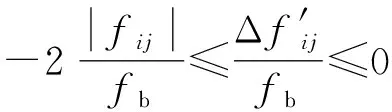
根据上述a和b这2种情况,线路i-j功率增量标幺值计算方法如下:
(22)
对于电力系统而言,转移潮流最理想情况是按照线路剩余的容量裕度进行分布,本文定义转移潮流裕度占用比为:
(23)

线路容量裕度计算如下:
(24)
其中,fs,max为线路s允许通过的功率最大值;fs,basic为线路s正常运行时通过的功率。
对式(23)的结果进行归一化处理:
(25)
其中,n1为在线路k断开后线路流通功率增加的线路数。
则由信息熵[13]的定义,系统的潮流转移分布熵可采用下式计算:
(26)
其中,Ht,k为线路k断开后系统潮流转移分布熵;c为常数,本文取值为1。
结合信息熵的相关知识可知,当某线路断开后,其余正常运行线路的转移潮流裕度占用比相等时,线路潮流转移分布熵取最大值,这也是线路断开引起潮流变化最均衡的状态,此时,容量裕度大的线路,其潮流增量相对较大,容量裕度小的线路,其潮流增量相对较小,这表明线路断开引起的潮流增量按照线路容量裕度大小均衡地分配于各线路中;反之,当线路断开引起的潮流增量均集中在某条线路上,而其余线路均不受影响时,线路潮流转移分布熵最小,此时是潮流分配最不均衡的状态。
可见,潮流转移分布熵可以用来衡量某线路断开后系统中其他线路潮流变化的均匀程度,该指标值越小,线路潮流转移按照线路容量裕度分布越不均匀,对系统的潮流冲击越明显,系统发生连锁故障的可能性越大。反之,潮流分布熵越大,线路潮流转移按照线路容量裕度分布越均匀,对系统的潮流冲击越不明显,系统发生连锁故障的可能性越小。
2.2 负荷冲击灵敏度熵
电力系统负荷非定值,当负荷变化时,系统中各线路都可能受到冲击,但各条线路受到潮流冲击情况不同,而针对不同负荷冲击,线路受到冲击量越大且变化越剧烈,线路越容易发生故障[6]。此外,若线路本身抵抗干扰的能力很强,即该线路很难出现越限断线的情况,此时考虑线路断开对其余线路影响的必要性不大,故需要对线路的抗干扰能力进行适当评估。本文仿照能量熵[14]的定义,定义负荷冲击灵敏度熵来评估线路的抗干扰能力。
设负荷节点a受到单位负荷冲击时,支路k潮流变化量为|ΔPk,a|。则负荷节点a受到单位负荷冲击时,系统的潮流变化总量为:
(27)
其中,ΔPk,a为负荷节点a受到单位负荷冲击时线路k潮流变化量。
类似于能量熵[14],负荷节点a的负荷扰动在线路k的负荷冲击灵敏度熵为:
(28)
则系统中负荷节点的负荷扰动在线路k的负荷冲击灵敏度熵为:
(29)
其中,n2为系统中负荷节点的数目。
(30)
对于系统中任意线路,当系统负荷节点受到单位负荷冲击后,该线路上的潮流变化量与所有线路潮流变化量之和的比值总是相同时,此时线路的负荷冲击灵敏度熵取得最大值,这也说明了该线路潮流会随着多个负荷节点的负荷变化而波动,这是线路对节点负荷变化最敏感的状态;反之,该线路上的潮流变化量与所有线路潮流变化量之和的比值差异较大时,潮流转移分布熵较小,此时也为线路对节点负荷变化最不敏感的情况。
上述构建的负荷冲击灵敏度熵指标,用来描述线路对负荷变化的灵敏程度。线路k的负荷冲击灵敏度熵Hs,k反映了支路k承担负荷节点负荷冲击后受到的功率冲击程度,其值越大,表明支路k对负荷节点的扰动越灵敏,支路越易发生开断故障;反之,其值越小,表明支路k对负荷节点的扰动越不灵敏,支路可靠性程度越高。
2.3 关键线路综合评价指标
由上文可见,线路潮流转移分布熵表征了系统中某线路断开后对其他线路的潮流冲击程度,负荷冲击灵敏度熵则表征了线路对负荷冲击的敏感程度。某些线路断线后对系统潮流冲击很大,但是其抵抗扰动的能力很强,该类线路对系统威胁相对较小;而某些线路断开后对系统潮流冲击并非很大,但是其抵抗扰动能力相对较弱,容易发生开断事故,此类线路对系统威胁则相对较大。故本文进一步综合考虑两者,得到线路的综合评价指标。
在定义线路综合评价指标之前,首先对线路潮流转移分布熵和负荷冲击灵敏度熵的结果进行归一化处理,归一化方法如下:
(31)
(32)
其中,n1为待归一化Ht,k的总数目;n2为待归一化Hs,k的数目。
线路潮流转移分布熵越小,该线路断开后对系统潮流冲击越大;负荷冲击灵敏度熵越大,则该线路对负荷节点负荷变化越灵敏,线路抵抗外界干扰的能力越低。故定义线路的综合指标为:
(33)

本文权重确定采用主客观权重确定方法,具体可参考文献[15]。在实际运用中,可以根据系统运行工况及行业专家的意见进行调整。则可知综合评价指标越大,线路的关键性越高,反之,线路的关键性越低。
3 关键线路识别流程及攻击方式
为分析识别结果的正确性,本文采用静态攻击方式,并以系统的输电效率[16]为考察指标来验证合理性,输电效率计算方式可参考文献[16]。
具体关键线路识别流程如下:
a. 读取系统的网络拓扑结构参数,求取电力系统的拉普拉斯矩阵;
b. 根据系统的拉普拉斯矩阵及矩阵谱分解方法求取拉普拉斯矩阵的广义逆矩阵,并求解有效电阻矩阵;
c. 根据本文所提方法计算各条线路的潮流转移分布熵和负荷冲击灵敏度熵,并计算出各线路的综合评估指标;
d. 根据所求各线路的综合评估指标进行排序,获得系统的关键线路;
e. 采用静态攻击方式对识别的关键线路进行仿真验证。
4 算例分析
4.1 算例验证
为验证所提方法的有效性,本文采用IEEE 39节点系统进行算例验证。图1为IEEE 39节点系统接线图,该系统共有39个节点、46条线路,其中线路2-30、6-31、10-32、16-19、19-20、19-33、20-34、22-35、23-36、25-37、29-38断开之后系统会发生解列,故不再考虑上述线路断开后潮流转移情况。

图1 IEEE 39节点系统拓扑图Fig.1 Topology of IEEE 39-bus system
将本文方法计算得到的线路潮流转移情况与采用断线模拟法[6-7]计算得到的结果对比分析,结果如表1所示。从表1可以看出,采用本文方法与采用断线模拟法所得结果一致,证明了本文方法计算转移潮流量的正确性。
表2为采用本文方法识别得到的IEEE 39节点系统关键线路与其他文献识别结果的部分对比。

表2 关键线路识别结果对比Table 2 Comparison of key lines identification results
从表2可以看出,采用本文方法得到的结果与文献[17]中的结果排名前6位的线路有5条相同,仅排序有所差异,说明本文方法对系统中的关键线路有一定的识别作用,结果的差异主要是由考虑因素不同造成的。文献[17]的潮流转移熵指标仅考虑了线路断开后系统中潮流冲击情况,而本文潮流转移分布熵考虑了线路断开后系统中转移潮流按照剩余线路容量裕度分配的均衡程度,并且本文方法也计及了各条线路抵抗干扰的能力。
结合图1可见,从网络拓扑结构来看,本文识别得到的关键线路大都属于系统内的联络线路,线路26-28和线路26-29或线路16-24和线路16-21断开后,39节点系统分解为两部分系统,正是由于这些线路是两部分系统的联络线路,当这些线路中任意一条故障后都会对系统造成较大的潮流冲击。此外,由表2中也可知,上述线路均有很高的负荷冲击灵敏度熵,说明了这部分线路对系统负荷的变化灵敏度较高,也一定程度上从侧面印证了这些线路的联络能力。
通常情况下,通过关键性指标识别出来的关键线路还需要一定的方法验证其有效性,本文采用10次针对性静态攻击,攻击后的输电效率如图2所示。

表1 本文方法与断线模拟法计算结果对比Table 1 Comparison of calculation results between proposed method and broken line simulation method
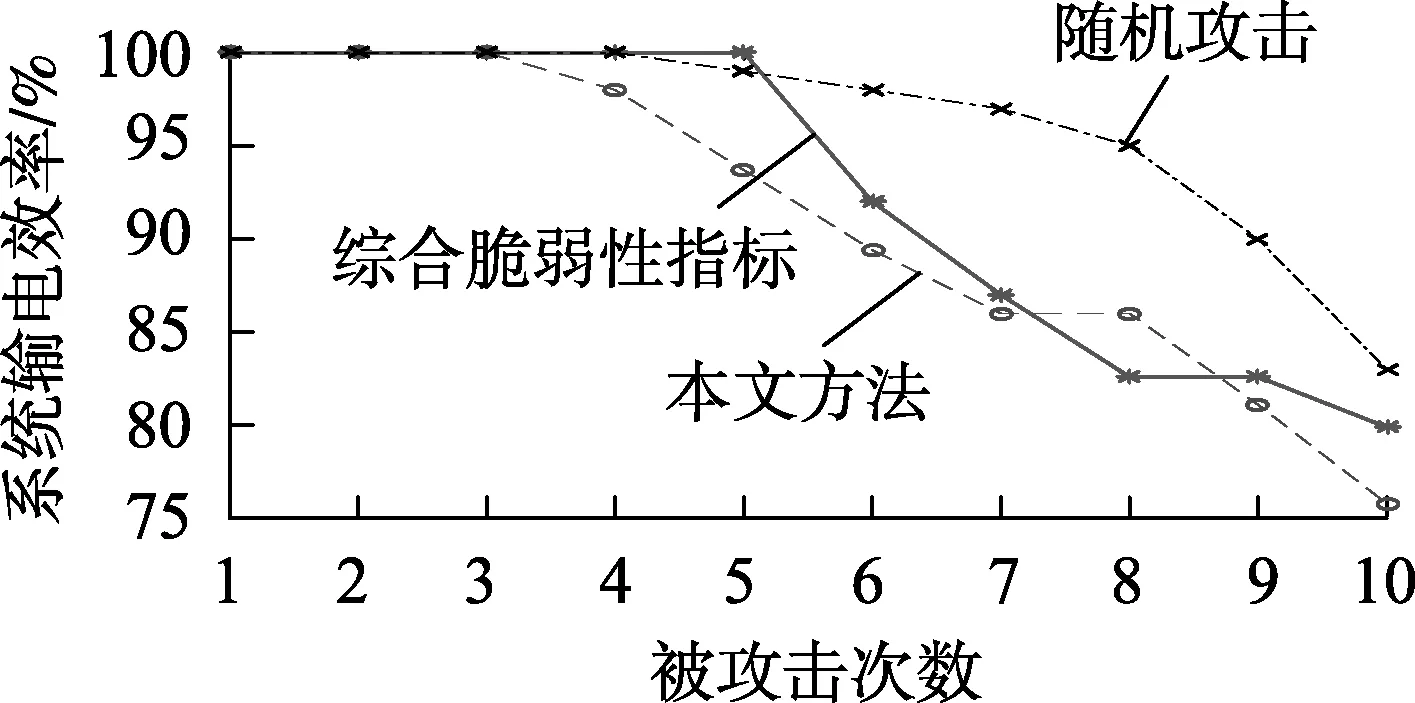
图2 系统输电效率Fig.2 System power transmission efficiency
从图2中可以看出,本文方法识别的关键线路在针对性攻击下输电效率基本呈线性下降,在第6次针对性攻击之后系统输电效率已经降至90%以下,在第10次攻击后则下降至75%左右;基于综合脆弱度指标[18]识别所得的关键线路,系统输电效率下降也十分明显,但下降速度相对较慢;而随机攻击时,系统则表现出较强的鲁棒性。由此可以说明本文方法在寻找关键线路时的有效性。
4.2 应用前景分析
通过对IEEE 39节点系统的分析表明本文提出的方法对系统中的关键线路有一定的识别作用。本文方法以网络拓扑结构为基础,在网络拓扑结构已知的情况下,可快速、准确地计算得到系统的关键线路,在实际工程中,由于广域测量系统的广泛应用,系统网络拓扑结构参数获得十分方便[14],因此,本文所提方法有一定实际意义。
关键线路分析中,线路的潮流转移熵日益成熟,但目前仍大多采用模拟线路断开的方法,本文方法虽无法分析令系统解列线路的潮流转移情况,但可以大幅减少实际系统中模拟线路断开的计算量,与现有方法进行适当结合则有望应用于实际系统中。
5 结论
a. 本文从直流潮流入手,得到系统的有效电阻矩阵,并根据有效电阻矩阵给出了线路断开后潮流转移的计算方式,为统一分析,对该计算方式进行了修正,在确定潮流转移区域的同时可以有效表征转移潮流的大小。
b. 本文根据线路的容量裕度对潮流转移熵进行改进,该指标可以有效表征线路断开后转移潮流按照剩余线路容量裕度分布的均匀程度,其值越小,转移潮流分布越不均匀,该线路断开后越容易引发连锁故障;此外,提出了负荷冲击灵敏度熵,该指标评估了线路对各负荷节点的灵敏度,其值越大,线路对节点负荷灵敏度越高,负荷出现扰动后,线路潮流波动越大,越容易引发连锁故障。
c. 综合考虑潮流转移分布熵和负荷冲击灵敏度熵,提出了关键线路识别的综合指标。对IEEE 39节点系统算例的分析结果表明,本文提出的识别方法能够识别出系统的关键线路。

