基于PWM波形特征的励磁涌流识别方法
胡 松,江亚群,黄 纯,高云鹏
湖南大学 电气与信息工程学院,湖南 长沙 410082)
0 引言
差动保护是电力变压器的主保护。随着变压器的容量越来越大,变压器差动保护的快速性和可靠性面临着严峻的挑战。励磁涌流与变压器区内故障电流的识别一直以来都是变压器差动保护研究的重点。目前工程上主要利用2次谐波原理[1]、间断角原理[2]和波形特征原理[3-8]识别励磁涌流。但是近年来由于励磁涌流造成变压器保护误动的案例不在少数,因此有必要进一步寻求更快速和高效的励磁涌流识别方法。
近年来,国内外学者提出了不少新的励磁涌流识别方法。文献[9]利用构造的平行四边形来识别励磁涌流,但是该方法对采样频率要求高,计算量大且对计算精度要求高。文献[10]提出了在直方图的基础上利用波形分布特征来识别励磁涌流。该方法原理简单、计算量小、灵敏性好,但是抗干扰能力不强,在电流互感器饱和等情况下该判据会失效。文献[11]利用Prony算法拟合基波和2次谐波的能量式,利用基波能量与2次谐波能量之比在发生区内故障时远大于励磁涌流的原理来识别励磁涌流,但是当发生严重的区内故障以及存在直流偏磁和电流互感器饱和时,2次谐波能量很大,会使该方法失效。
本文利用励磁涌流的波形特征,将信号波与载波进行调制,通过得到的脉冲宽度调制(PWM)波形的特点来识别励磁涌流。本文提出了2个励磁涌流识别判据,双判据的综合使用可以准确地识别各种情况下的励磁涌流,与2次谐波制动法和间断角识别方法相比,本文所提方法的灵敏度更高,且识别时间短。
1 励磁涌流及其PWM波形特点
1.1 励磁涌流波形特点
励磁涌流含有非平稳波峰及大量的非周期分量,且波形之间存在间断,其波形与正弦波存在较大差距[12-13],如图1所示。根据调制法原理可知,信号波与载波信号进行调制时,会得到与信号波冲量相等的PWM波形。若信号波为正弦波,与等腰三角形载波进行调制时会得到一系列等幅不等宽的PWM波形,且其宽度按正弦函数变化。当信号为励磁涌流时,由于间断角及非周期分量的存在,其产生的PWM波形会有一段长时间的缺失,且PWM波形的脉冲分布与正弦波调制产生的PWM波形也有较大不同,因此可利用该特点识别励磁涌流。
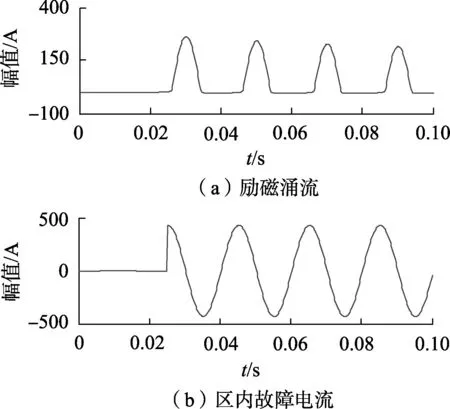
图1 励磁涌流与区内故障电流Fig.1 Inrush current and internal fault current
1.2 PWM波形的获得
取差流在1个工频周期内的采样数据x(i)(i=1,2,…,N,本文取N=80,即采样频率为4 000 Hz),然后进行下列处理。
a. 对1个工频周期内的采样数据进行滤波去噪,然后进行取绝对值和归一化处理,得到:
(1)
b. 产生等腰三角形锯齿波载波p(i)(i=1,2,…,N),载波比为20(即载波信号的频率为1 000 Hz,周期为1 ms),幅值为1.1。
c. 按下列原则调制产生PWM波:
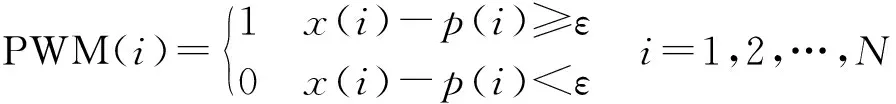
(2)
其中,ε为附加系数。
正常情况下,受各种因素的影响,差流并不为0,而是接近于0,为了消除这种影响,本文中取ε=0.01。
2 励磁涌流识别判据
2.1 励磁涌流识别判据1
图2、图3分别为按照第1节方法对区内故障电流和励磁涌流进行处理后产生的PWM波形,图中,纵轴为标幺值。

图2 区内故障电流及其PWM波形Fig.2 Internal fault current and its PWM waveform

图3 励磁涌流及其PWM波形Fig.3 Inrush current and its PWM waveform
由调制特性可知,当一段连续正半弦波与载波进行调制时,PWM波幅值为0的区间不会超过1个载波周期(即1 ms), 经过取绝对值处理后进行调制,PWM波幅值为0的区间也不会超过2个载波周期。区内故障电流的PWM波幅值为0的区间出现在故障电流过零点,正好对应载波零点,如故障角为0°的情况下,取绝对值时区内故障电流的PWM波形在2个载波周期内为0,但不会超过2个载波周期。而励磁涌流中存在间断角,调制产生的PWM波幅值在间断角期间为0,时间较长。故设置励磁涌流识别判据1如式(3)所示(为便于叙述,下文简称判据1)。
ΔT≥2.5 ms
(3)
其中,ΔT为PWM波形幅值为0的区间的最大长度。
由于载波信号周期为1 ms,考虑一定的裕量系数,本文阈值取2.5 ms,而2.5 ms对应1个工频周期的角度为45°,且其中还包含了信号波本身比载波小的部分,实际上当间断角小于45°时也可能满足判据1,但不存在间断角时肯定不满足该判据。判据1极大地减小了利用间断角原理识别励磁涌流的阈值,使得励磁涌流识别更加快速、准确。
2.2 励磁涌流识别判据2
在对称性涌流或电流互感器饱和等情况下,励磁涌流间断角将减小甚至消失,或者出现上下偏移的情况,导致判据1失效(如图4所示,其中图4(b)、(c)的纵轴为标幺值)。

图4 电流互感器饱和时的励磁涌流及PWM波形Fig.4 Inrush current and PWM waveform when CT saturation occurs
取一段标准工频正弦波最大值到最小值及其之间半周期的采样数据(1个周期采样80点,则最大值与最小值及其之间数据为41点),进行滤波和归一化处理;同时,从待分析信号1个周期的采样数据中取出最大值与最小值及之间的数据进行滤波和归一化处理。若待分析信号的最大值与最小值之间的采样点数不足41点,不足的点通过在后面补0获得;若采样点数超过41点,只取前41个采样点。若待分析信号在采样的起点处为最大值,则将标准半周期正弦采样数据减去待分析信号采样数据;若待分析信号在采样的起点处为最小值,则将标准正弦波的采样值取负后再与待分析信号的采样值作差。最后,将得到的差值取绝对值后再与载波进行调制。
图4所示的励磁涌流和图2所示的区内故障电流的最值间半周期数据差调制得到的PWM波形分别如图5和图6所示,图中,纵轴均为标幺值。

图5 电流互感器饱和时励磁涌流与标准正弦波的半周期数据差及PWM波形Fig.5 Difference between inrush current and standard sine wave in half cycle and PWM waveform when CT saturation occurs

图6 区内故障电流与标准正弦波的半周期数据差及PWM波形Fig.6 Difference between internal fault current and standard sine wave in half cycle and PWM waveform
由图5、6可见,区内故障电流的最值间半周期数据差很小,调制得到的PWM波形幅值为1,矩形波个数少甚至为0,且脉宽很小,而励磁涌流最值间半周期数据差很大,调制得到的PWM波形幅值为1、矩形波个数多且脉宽较大。据此提出励磁涌流识别判据2,见式(4)(为便于叙述,下文简称判据2)。
(4)
其中,Ti为第i个PWM波形幅值为1的脉宽;n为PWM波形幅值为1的脉宽总数;Tset为阈值。
判据2用于统计半个工频周期内PWM波形中幅值为1时的宽度,当总宽度大于等于设定的阈值Tset时,判断为励磁涌流,否则判断为区内故障电流。
综合利用判据1、2进行励磁涌流识别:当满足判据1时,直接判断为励磁涌流;当不满足判据1时再利用判据2来识别励磁涌流。
判据1、2的配合使用,可以快速有效地识别出励磁涌流与区内故障电流。利用调制法得到的PWM波形来识别励磁涌流,原理简单,灵敏度高,能准确识别各种情况下的励磁涌流,其励磁涌流识别流程如图7所示。

图7 励磁涌流识别流程图Fig.7 Flowchart of inrush current identification
3 仿真验证及分析
3.1 仿真模型的建立

图8 仿真模型Fig.8 Simulation model
利用PSCAD建立如图8所示的仿真模型。其中,变压器采用铁芯饱和型变压器模型,变比为220 kV/110 kV,容量为80 MV·A,变压器饱和参数设置为空心电抗为0.2 p.u.,瞬变衰减时间常数为1 s,膝电压为1.25 p.u.,释放磁通削减时间为0.1 s,磁化电流为2.0%;电流互感器变比为600 A/5 A。利用PSCAD对不同合闸角和考虑电流互感器饱和情况下的变压器空投、不同类型区内故障等进行仿真实验[14-16],获得相应的变压器差流波形,再将波形数据导入MATLAB中进行数据处理与分析。
3.2 仿真分析
对称性涌流及PWM波形见图9,图9(b)、(c)的纵轴为标幺值。由图9可见,在1个工频周期内,对称性涌流的PWM波形幅值为0的区间最大长度为4.75 ms,大于阈值2.5 ms,则满足判据1;最大值和最小值间的半周期采样数据与正弦半周期数据求差后,调制得到的PWM波形幅值为1的脉宽和为5 ms。

图9 对称性涌流及PWM波形Fig.9 Symmetrical inrush current and PWM waveform
非对称性涌流及PWM波形如图10所示,其中图10(b)、(c)的纵轴为标幺值。由图10可见,变压器空投时单向偏向一侧非对称励磁涌流1个周期内调制所得PWM波形幅值为0的区间最大长度为8.75 ms,最大值与最小值之间的半周期采样数据与正弦半周期数据求差后,调制得到的PWM波形幅值为1的脉宽和为3.5 ms。

图10 非对称性涌流及PWM波形Fig.10 Asymmetric inrush current and PWM waveform
发生区内单相接地时的故障电流及PWM波形如图11所示,其中图11(b)、(c)的纵轴为标幺值。由图11可见,1个工频周期内的区内故障电流调制得到的PWM波形幅值为0的最大区间长度为0.75 ms,最大值与最小值之间的半周期采样数据与正弦半周期数据求差后,调制得到的PWM波形幅值为1的脉宽和为0。

图11 区内单相接地故障电流及PWM波形Fig.11 Internal single-phase grounding fault current and PWM waveform
由上述分析可见,判据1可以识别大部分的励磁涌流。为了更好地区分区内故障电流与励磁涌流,判据2的阈值Tset取1.25 ms。通过大量仿真实验证明,区内故障电流与励磁涌流测得的数据与2个判据的阈值存在明显差距。因此,利用调制得到的PWM波形特征能够准确地识别励磁涌流。
表1列出了在不同合闸角下的变压器空投时的ΔT和∑T的值,表2列出了发生不同类型的区内故障时ΔT和∑T的值。由表1、2可见,设定的2个判据阈值可有效区分励磁涌流与区内故障电流。
对于不同类型(双绕组/三绕组/自耦、单相/三相共体/三相分体)、不同参数(容量、电压等级、变比及其他参数)的变压器,其励磁涌流和内部故障电流具有相同的PWM波形特征,因此可以采用相同的阈值进行有效识别。

表1 不同合闸角时的励磁涌流识别仿真结果Table 1 Simulative results of inrush current identification with different switching angles

表2 不同类型区内故障的仿真结果Table 2 Simulative results of different internal fault

图12 发生电流互感器饱和时的区内故障电流及PWM波形Fig.12 Internal fault current and PWM waveform when CT saturation occurs
3.3 抗电流互感器饱和分析
在系统发生故障时,由于非周期分量与剩磁等因素的影响,容易发生电流互感器饱和。电流互感器饱和对变压器差动保护影响很大,在已有的励磁涌流识别方法中较少考虑到电流互感器饱和因素。图12为发生电流互感器饱和时的区内故障电流的PWM波形(图12(b)、(c)纵轴为标幺值),其ΔT=0.75 ms、∑T=0.25 ms,都不超过对应的判据阈值。图13为发生电流互感器饱和时励磁涌流的PWM波形(图13(b)、(c)纵轴为标幺值),其ΔT=3.75 ms、∑T=5.25 ms,均大于对应的判据阈值。
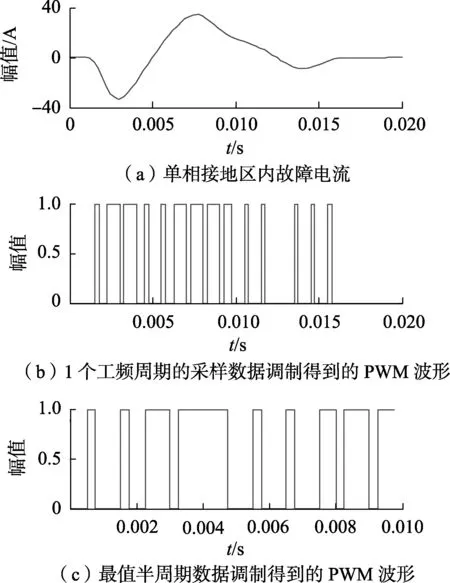
图13 发送电流互感器饱和时的励磁涌流及PWM波形Fig.13 Inrush current and PWM waveform when CT saturation occurs
因此可以看出利用调制所得PWM波形特征来识别励磁涌流的方法具有一定的抗饱和性。
4 结论
本文在分析励磁涌流与变压器区内故障电流波形特征的基础上,提出了一种基于PWM波形特征的励磁涌流识别方法。该方法利用调制得到的PWM波形特征识别励磁涌流。通过计算采样1个工频周期数据调制得到的PWM波形幅值为0的区间最大长度,以及最值间半周期数据差调制得到的PWM波形幅值为1的脉宽和,设置了2个有效区分励磁涌流和区内故障电流的阈值。大量仿真表明本文方法简单有效,灵敏度高,识别时间短,并具有一定的抗电流互感器饱和能力。

