多换流器并联的交直流配电网潮流计算方法
彭 克,张 聪,陈 羽,徐丙垠,赵艳雷
山东理工大学 电气与电子工程学院,山东 淄博 255000)
0 引言
目前我国配电网主要采用交流电网作为供电载体,但是随着负荷的日益增长,交流电网的规模不断扩大,其运行控制过程愈发复杂,系统的安全稳定问题越来越严重。同时,面对电动汽车、分布式电源(如光伏)以及LED照明等直流设备的大规模接入,交流电网的电能变换环节增多,供配电的效率受到影响。
近年来的研究成果表明[1-2],基于柔性直流技术的交直流混合配电网更适应现代城市配电网的发展,电力电子装置使得配电网的组网形态及控制方式更加灵活多样,直流系统通过DC/DC变换装置等可实现不同电压等级之间的互联,换流器的灵活控制方式可以实现交直流潮流的相互转供,有利于系统的可靠稳定运行,未来的智能配电网将会是一个交直流全面互联的复杂系统,一方面其可与上层交直流混合输电体系相协调,另一方面可就地接入直流分布式电源与负荷,满足配电网的直流源荷接入需求。
目前,关于交直流配电网的研究还存在大量的理论与技术问题有待解决[3-5]。系统潮流是分析众多问题的基础,因此在潮流控制与计算方法方面已有学者展开了相关研究,文献[6-9]从换流器的控制策略以及换流站运行方式等多个方面探讨了交直流配电网的潮流计算方法;文献[10]提出了多端互联的交直流配电网分层潮流控制策略,并提出了采用下垂控制的高斯-牛顿交直流混合潮流算法;文献[11]分析了交替迭代算法需要多次交替进行的原因,提出了一种适用于电压源换流器型混合电网的交直流解耦潮流算法。但上述研究均未考虑换流器并联的情形,而实际工程中如加拿大纳尔逊河直流工程及美国太平洋联络线直流工程[12-13]采用了两端并联的结构。由于一条直流母线上存在2个或多个换流器,其各自的控制策略均需要控制直流母线电压,因此需进行相应的协调处理。文献[14]提出了附加直流电流平衡控制功能的协调控制方式,避免了各换流器对电压控制的争夺,但其附加控制方式较为复杂。
可采用下垂控制对并联换流器进行协调,利用各换流器的下垂曲线将直流母线电压控制在同一数值,目前开展的相关研究主要侧重于装置级的策略,如并联换流器的环流抑制等,但在系统级的稳态分析以及优化调方面少有研究。当两端或多端直流配电系统中存在并联换流器时,需获知每一个换流器的运行状态,以便对换流器下发调度指令满足负荷需求,因此需要计及各个换流器的状态量进行潮流计算。当采用下垂控制时,各个换流器均需按照下垂曲线参与计算进行求解,即在平衡节点处存在多个电压控制源且需收敛于同一电压值,而目前研究的算法一般是考虑单一换流器采用下垂控制的情形进行计算,这显然已经难以适用于多换流器并联的情形。
本文针对上述难题展开研究,提出了基于虚拟主从策略的多换流器并联潮流计算方法。首先探讨了交直流配电网的网络结构及控制策略,然后针对多换流器并联的情形进行了算法设计。将多换流器并联的直流母线视为平衡节点,利用该节点上的功率平衡方程及Udc=f(P)下垂特性方程,推导得到首编号换流器有功功率与其他换流器下垂曲线的关系式,实现该换流器的功率求解,从而按照Udc=f(P)下垂曲线获取直流电压值,其他编号的换流器利用该电压并按照P=f(Udc)下垂曲线进行有功功率更新,解决了多换流器同时控制平衡节点电压的潮流计算难题。由于首编号换流器负责直流电压计算,因此在算法设计中将该换流器定义为虚拟主换流器,其他换流器定位为虚拟从换流器,以方便进行计算与程序设计。最后通过算例测试验证了本文所提算法的有效性和正确性。
1 交直流配电网拓扑与控制策略
对于网络拓扑结构而言,柔性直流配电系统的基本拓扑结构主要有两端供电方式和多端供电方式2种。图1为一示范工程拟采用的两端直流配电网拓扑结构,AC/DC换流器并联于中压直流母线上,分别通过DC/AC换流器以及DC/DC换流器对低压交流及直流负荷供电,同时配置代理(Agent)装置采集低压交、直流负荷信息,供上层管理系统对3个AC/DC换流器进行优化调度。

图1 多换流器并联的交直流配电网拓扑Fig.1 Topology of AC-DC hybrid distribution network with multi-converter in parallel
在具体的控制策略方面,3个AC/DC换流器均采用下垂控制,即根据有功功率与直流电压的线性关系,通过下垂系数协调不同换流器的功率输出,该控制策略基于有功功率与直流电压的线性关系协调各换流器的有功功率输出,无功功率按照单位功率因数控制。图2给出了Udc-P下垂控制原理。

图2 Udc-P下垂控制原理Fig.2 Principle of Udc-P droop control
根据图2所示下垂控制曲线可得到换流器功率Udc=f(P)的下垂表达形式:
(1)
对式(1)进行变化可以得到式(2)所示的P=f(Udc) 下垂表达形式。
(2)
其中,K为直流电压下垂系数;Udc和Udcref分别为直流侧母线电压和直流侧母线电压参考值;Udcmin和Udcmax分别为换流器直流侧母线电压允许的最小直流电压和最大直流电压;Pmax为工作于整流状态的换流器最大输出有功功率;Pmin为工作于逆变状态的换流器最大输出有功功率。当低压交直流系统的功率发生波动时,各换流器之间根据下垂特性协调有功功率输出,实现负荷的重新分配以及直流母线电压的稳定。
按照示范工程的要求需对中压AC/DC换流器进行优化调度,则需对每个换流器进行最优潮流或者潮流计算给出换流器指令,但会出现多个换流器按照各自的下垂曲线同时控制直流母线电压且需收敛至同一电压值的情况,常规潮流计算方法难以计算,需探索新的潮流计算方法。
2 算法设计与实现
交流配电网的潮流计算方法有牛顿法、Zbus高斯算法、前推回代法等。其中Zbus高斯算法是以系统节点导纳矩阵为基础的一种潮流算法,其原理比较简单,要求的内存量也比较小,相比于前推回代法,其对环状网络的求解具有较大的优势,虽然是一阶收敛的算法,但具有接近牛顿法的收敛速度以及收敛特性。Zbus高斯算法对于一般的配电系统具有较好的适应性。
采用Zbus高斯算法时,交流配电系统与直流配电系统的节点电压方程均可写成如下形式:
(3)
其中,I1、U1分别为平衡节点的电流和电压向量;I2、U2分别为其他节点的电流和电压向量;Y11为平衡节点的自导纳矩阵;Y12、Y21为平衡节点与其他节点的互导纳矩阵;Y22为其他节点的自导纳矩阵。
一般而言,常规交流配电系统的平衡节点电压是给定的,除平衡节点外其他节点的电压可用式(4)计算。
(4)
对于直流配电系统而言,当多个换流器采用下垂控制并联接入同一母线时,该节点作为平衡节点,其直流电压不再是给定值,而是由各换流器的下垂曲线共同决定。假设该母线上接有m个换流器,则根据式(1)有:
(5)
该母线上的总负荷功率与换流器功率满足式(6)所示关系。
PLoad=P1+P2+…+Pm
(6)
式(5)共有m-1个有效方程,与式(6)联立构成m个方程,可求解得到每个换流器的有功功率,进而可计算得到该母线的电压。
若系统中有n条采用下垂控制的母线,每条母线接有m个换流器,按照上述分析需要求解n×m个方程,考虑到换流器并联于同一直流母线,在设计下垂曲线时一般有Udcref1=Udcref2=…=Udcrefm,联立推导式(5)、(6),可得到换流器1的有功功率具有如下规律:
(7)
因此,可利用式(7)直接求取换流器1的有功功率,进而通过该换流器的下垂曲线计算直流母线电压Udc,其他换流器根据直流母线电压更新其有功功率。在算法设计过程中,可选定首编号换流器(如换流器1)作为虚拟主换流器更新电压,而其余换流器作为虚拟从换流器更新有功功率,这样可避免多个换流器同时依据各自的下垂曲线Udc=f(P)计算电压导致的无法求解的难题。
以第k+1次迭代过程为例给出具体的步骤,具体流程如图3所示。

图3 算法流程Fig.3 Flowchart of algorithm
a. 利用第k次迭代过程的直流电流求解非平衡节点的第k+1次的直流电压:
(8)



e. 根据式(1)所示的Udc=f(P)下垂曲线计算平衡节点电压,有:
(9)
f. 根据P=f(Udc)下垂曲线的表达式计算各虚拟从换流器的有功功率,有:
(10)
其中,下标ih表示第i个平衡节点上的第h个虚拟从换流器。

宝玉爹喜欢坐一把木质靠背椅,这椅子很沉,墨黑墨黑的,后面的靠背呈弧形,上面雕了花,还有兽物什么的,据说是他祖上留下来的,人称太师椅。可惜的是,文化大革命的时候,一夜间当上了“全无敌”战斗兵团司令的二狗伢,说那是四旧,封、资、修,派了两个打手,强行将椅子抢走,砸烂,烧了,那是后话。

i. 求解交流节点电压方程:
(12)

j. 更新交流平衡节点注入电流与功率。
k. 判断直流系统及交流系统是否收敛,即判断系统中各个交流节点电压与直流节点电压是否满足式(13)。若式(13)成立,则计算收敛结束;否则返回步骤a继续迭代计算。
(13)
其中,ε为给定的潮流迭代误差向量。
3 算例测试
基于天津大学PFDG软件平台实现本文所提算法,为了验证所提算法的正确性,采用图1所示交直流系统,考虑实际运行中的控制策略,将代理设备所监控的低压系统进行等效,并在DIgSILENT软件中搭建了如图4所示的算例进行暂态仿真验证,其中负荷L1的功率为485 kW,负荷L2的功率为1 000 kW,换流器参数如表1所示(表中直流电压参考值、直流功率参考值为标幺值,后同)。

图4 测试算例Fig.4 Test case
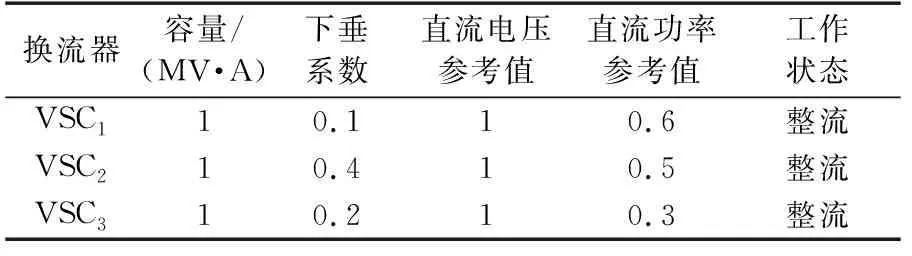
换流器容量/(MV·A)下垂系数直流电压参考值直流功率参考值工作状态VSC110.110.6整流VSC210.410.5整流VSC310.210.3整流
3.1 算法验证
首先在DIgSILENT软件中搭建测试算例的暂态仿真模型进行计算以便验证本文所提算法,表2给出了本文所提算法的计算结果与DIgSILENT软件达到稳态时的计算结果(直流电压为标幺值)。由表2可以看出,本文所提算法的计算结果与DIgSILENT软件的计算结果基本吻合,验证了本文所提算法的正确性。

表2 计算结果比较Table 2 Comparison of calculative results
3.2 虚拟从换流器退运
虚拟从换流器VSC3退出运行,直流负荷由VSC1与VSC2共同承担,该情况下本文所提算法的计算结果如下:VSC1功率为0.908 0 MW,VSC2功率为0.577 0 MW,直流电压为0.969 2 p.u.。
由计算结果可以看出,VSC1与VSC2共同分担了直流负荷,但由于VSC1的下垂系数较大,导致2个换流器的有功功率分摊相差较大,因此合理地选择下垂系数有利于换流器之间的功率协调。
3.3 虚拟主换流器退运
当虚拟主换流器退运时,算法会依据换流器编号依次选定下一换流器作为虚拟主换流器进行计算,在图4所示算例中,当VSC1退运后,算法会选择VSC2作为虚拟主换流器,该情况下的计算结果如下:VSC2功率为0.728 3 MW,VSC3功率为0.756 7 MW,直流电压为0.908 7 p.u.。
因为VSC2与VSC3的下垂系数相差不大,因此2个换流器近似均分功率,但是由于这2个换流器的功率输出均增大,根据下垂曲线进行控制时导致电压降低(为真实输出电压,计算该算例时未对电压进行限制)。通过该算例可以看出,下垂系数的选择还应考虑换流器退运情况下的电压过低或者越限问题。
3.4 IEEE 123节点算例测试
为了进一步验证本文所提算法的有效性,对文献[15]设计的交直流混合配电网算例进行测试与分析,该算例以IEEE 123节点系统为基础进行改造,在节点13与节点152、节点60与节点160以及节点54与节点94之间均并联2个换流器,具体结构如图5所示,系统参数可参见文献[15],换流器参数如表3所示。

图5 算例结构Fig.5 Structure of example
利用本文所提算法进行计算,所得结果如表4所示(表中电压为标幺值)。换流器VSC11、VSC12、VSC21以及VSC22工作于整流状态(功率为负),VSC31与VSC32工作于逆变状态(功率为正),6个换流器共同维持交直流系统之间的功率平衡,由此可见本文所提算法对规模较大的多端互联系统也具有较好的适应性。由于算例系统的电压等级较低,电压对功率变化的灵敏性较高,因此下垂系数不宜选取过大。
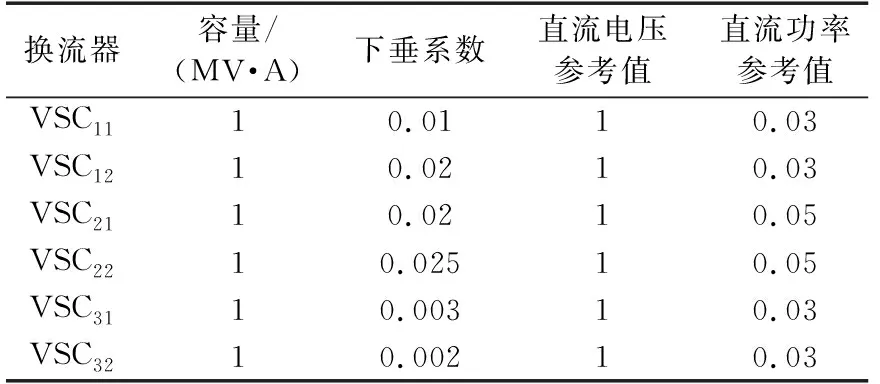
表3 换流器参数设置Table 3 Parameters of converters

表4 换流器有功功率及电压的计算结果Table 4 Calculative results of converter active power and voltage
4 结论
本文针对多换流器并联的交直流配电网潮流计算展开研究,提出了基于虚拟主从控制策略的潮流计算方法,并通过算例进行了验证,可以得到以下结论:
a. 通过并联换流器的下垂曲线方程推导得到主换流器有功功率与从换流器控制参数的关系式,从而实现母线电压与换流器功率的分离计算,解决了多换流器并联同时控制平衡点电压的潮流求解难题;
b. 根据换流器节点编号定义主、从换流器,即将首节点编号换流器作为主换流器,可以实现主、从换流器退运时潮流的有效计算;
c. 下垂系数的设计对并联换流器运行的影响较大,一方面要考虑正常运行时的功率分摊,另一方面还需考虑换流器退运时母线电压存在的过低或越限风险。
考虑到后续对换流器优化调度的需求,笔者将进一步开展计及网损、无功等多目标的交直流互联系统优化方法的研究。

