以分数阶微分为基础的尺度不变特征变换图像匹配算法分析

孙奇

（北京信息职业技术学院，北京 100018）

1 图像处理与匹配理论

1.1 分数阶微分

在计算机的视觉识别中，提取图像匹配特征的关键点，应提前保证图像的清晰度良好，图片模糊或纹理区域相对较弱的时候，图像特征不会特别突出，这将会直接造成难以准确提取图像的关键点，以此导致图像匹配的准确性大大降低。但是，分数阶微分能够以图像特征增强的方式，进一步解决这一不良现象。分数阶微分来源于古典微积分，从古至今发展形成了一定的表达式，即R-L定义、G-L定义和Caputo定义。其中，R-L定义与G-L定义都可以利用卷积形式计算数值，但是，G-L定义主要把微分阶次从整数限定条件向分数条件进行推广，所以，能够在很大程度上保证图像处理结果的精确度，并在各个领域得以广泛应用。本文通过利用G-L定义，处理图像特征。

1.2 分数阶微分

利用各种尺度的分数阶微分掩模算子，调节分数阶阶数，观察分数阶微分的图像增强效果。利用m×n算子，进行图像分数阶运算，以此增强图像。其中运算规则就是利用模板算子对m×n大小的图像通过相关公式，进行线性滤波。其中，一般模板大小m与n是相同的，而且都属于奇数。为了确保图像全方位接受滤波处理，需要对各个像素点加以处理。由于属于方形掩模，在其中心点距离图像边缘小于（n-1）/2个像素的时候，掩模行与列都会位于图像平面以外，图像的周围像素则无法进行滤波处理。而为了确保效果良好，在进行运算的时候，应该先填充图像，将边缘填充（m-1）/2行与（n-1）/2列，这样一来，则能对图像边缘的像素点进行分数阶微分计算。

1.3 尺度不变特征变换

所谓尺度不变特征变换图像匹配算法是由Lowe提出来的。利用SIFT算法所获取的特征关键点描述子与图像比例、旋转变化有较好的适应性，是现阶段最为有效的计算机视觉图像处理技术，而且在各个领域都实现了广泛应用。SIFT图像匹配算法整个流程包括五大步骤：（1）检测尺度空间的极值；（2）定位关键点；（3）匹配关键点的具体方向；（4）制造SIFT特征关键点描述子；（5）匹配SIFT特征。

1.3.1 检测尺度空间极值

因为SIFT算法需要在尺度空间上，提取图像特征关键点，所以，需要提前把图像向尺度空间内部转换，可以利用二维高斯函数和图像，通过卷积计算，把二维图像向尺度空间内部转换，具体的转换过程为：

其中，L（x，y，σ）代表尺度空间的图像；G（x，y，σ）代表高斯函数；I（x，y）代表原始图像；σ代表灰度空间的尺度因子。想要进一步检测尺度空间的极值，可以利用差分高斯函数和原始图像，通过卷积计算，获得尺度空间极值。

1.3.2 定位关键点

定位关键点，关键在于计算DoG函数的二次泰勒，同时利用以下公式对采样点进行计算：

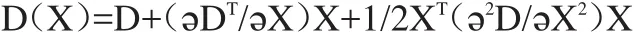
其中，X＝（x，y，σ），T代表极值点到样本数据点的偏移量，在X求导之后，取其中极值，获取极值点的具体位置。

1.3.3 匹配关键点方向

SIFT在变换时，都明确对图像局部特征的具体关键点进行方向设定，所以，可以实现图像旋转的不变性，在计算关键点方向的相关参数时，可以通过获取关键点相邻区域像素的梯度方向分布特性，以此确定关键点的梯度模值与方向，进一步明确匹配关键点方向。

1.3.4 构造SIFT特征关键点描述子

通过确定关键点的具体位置、尺度、方向参数，使在二维空间中图像局部特征不会发生变化。如果需要图像在光照变化与3D图像中不会发生变化，需要构造特征关键点描述子。在进行构造时，应先计算关键点周围的像素点梯度模值与方向，再利用关键点的尺度，进一步确定图像模糊高斯函数的尺度因子，然后调整描述子坐标与梯度方向，确保其与关键点保持在同一方向，以此保证旋转不会发生变化。

1.3.5 匹配SIFT特征

匹配SIFT图像特征的时候，应先确定首张图像的特定局部特征关键点，寻找此关键点到次张图像的最小欧氏间距以及次欧氏间距。如果最近间距与次近间距相除，获取的值在阈值以内，那么可以匹配图像中的两个关键点，阈值一般设定为0.8。

2 实验结果分析

想要进一步对分数阶微分的图像配准算法性能提升进行验证，应选择不同阶数，并匹配实验多幅图像。其中，选择灰度图像如图1-1所示，并旋转30°，获得图1-2所示，利用SIFT算法，提取图1的SIFT特征关键点，再匹配图像。通过利用RANSAC算法，对错误的匹配数进行判断。

图1 匹配图像

选取不同分数阶数的改进SIFT算法与原始SIFT匹配算法做实验比较分析，具体结果如表1所示。

就相关数据可知，使用分数阶微分与改进SIFT匹配算法能够获得更多关键点，以此提高匹配的正确率。在分数阶阶数在0.4的时候，在图1匹配中，关键点个数与正确匹配数最大，而且匹配率也得以明显提升。在0.8时，达到了最高状态。这就说明在分数阶微分中利用SIFT匹配算法，所检测的关键点个数与匹配数都会得到很大程度上的提升，其中错误配数也会有所减少，并大大提高图像匹配的准确率。

为了进一步证明SIFT算法的良好性能，选取图2，利用不同分数阶算子做匹配实验。

图2 匹配图像

表1 特征点数与匹配

通过利用5×5大小的分数阶算子进行实验分析，结果具体如表2所示。

就相关数据可知，分数阶微分与改进SIFT匹配算法的有效性较好，在阶数为0.6的时候，匹配对数最大，匹配率也有明显提高。在阶数为0.8的时候，匹配率能够达到最高状态。这说明改进SIFT算法可以在很大程度上提高关键点个数与匹配对数，以此促使匹配的正确率得到明显提升。

通过利用3×3大小的分数阶算子进行实验分析，结果具体如表3所示。

就相关数据可知，利用3×3大小尺度的分数阶算子，直接提高了SIFT匹配的关键点个数、匹配对数、匹配准确率，但是匹配效果与5×5大小尺度比较，相对较低。

通过图1和图2的结果统计比较分析，具体如表4所示。

就相关数据可知，在阶数为0.5-0.8的时候，匹配准确率相对较高，而且在0.8的时候达到了最高状态。这就说明利用分数阶微分与改进SIFT匹配算法，在选择合适的分数阶数时，既可以大大降低错误匹配率，又可以提高匹配准确率。

表2 特征点数与匹配

表3 特征点数与匹配

表4 结果分析统计

3 结语

在计算机视觉领域中，图像匹配是十分重要的组成部分，并且与人类日常生活密切相关。所以，随之衍生了大量图像匹配技术。随着基于局部特征描述子的提出，也就是尺度不变特征变换算法，其可以提取十分稳定的特征点，而且具备旋转不变特性，即使是目标旋转、平移、大小、光照等都可以保持不变。因此，SIFT算法在图像匹配中的应用越来越广泛。SIFT图像匹配算法主要是以局部特征为依据，合理选择特征匹配点，通过分数阶微数处理图像，可以明显提高图像的纹理细节特征，把分数阶微分与SIFT匹配算法有机结合，能够在很大程度上提高关键点数与匹配对数，使正确匹配率和SIFT算法效率得以提升。