基于距离徙动轨迹的空间目标ISAR联合运动补偿算法

俞 翔朱岱寅毛新华

( 1．南京工程学院计算机工程学院，南京，211167; 2．南京航空航天大学电子信息工程学院，南京，210016)

引言

逆合成孔径雷达( Inverse synthetic aperture radar，ISAR)成像技术是一种主动探测手段，可不受气象条件的影响远距离获取非合作目标的高分辨图像。近年来，公开发表的文献中就不乏对多类目标的ISAR成像研究成果［1-6］。本文针对空间高速运动目标，研究其脉内走动补偿和距离对齐即联合运动补偿问题。

高精度运动补偿是ISAR高分辨成像必须解决的关键问题。空间目标大多具有极高的运行速度，若目标在脉宽内的径向运动(脉内走动)距离与距离分辨率相比不能忽略，则经典的“停-跳”假设不再适用，而脉内走动会导致距离像散焦，降低图像的实际分辨率，因此，脉内走动必须加以补偿。现有脉内走动补偿算法主要利用单个脉冲估计瞬时多普勒［7-8］，而由于回波的个体差异，针对脉冲逐个校正的方法显然会引入随机误差，而且其算法精度和鲁棒性均受脉宽的限制。目标径向运动造成的距离像相对偏移也会导致图像方位向散焦，因此需要通过距离对齐算法校正。现有的距离对齐算法主要可以分为互相关对齐［9-11］和全局对齐［12-15］两类。前者在距离像相关性不强的情况下对齐效果不佳，而后者一般以某种全局优化准则作为代价函数，通过迭代的方法使代价达到最小值。虽然，通过插值可以在一定程度上提高现有距离对齐算法的精度，但距离偏移误差和高频相位误差的引入仍不可避免。这一方面导致了目标图像不同程度的散焦，另一方面，由于原始的回波相位历程被破坏，使得高分辨成像变得困难。

本质上，目标的距离像偏移和脉内走动都源于目标的距离徙动，即距离徙动相对于脉间和脉内是无差别的。据此，本文针对空间目标的运动特点，研究了目标的等效运动与距离徙动轨迹( Range migration trajectory，RMT)，并提出了一种基于目标RMT的脉内和脉间联合运动补偿算法。该算法依据全局熵最小化原则，首先从RMT中估计出目标的平动参数即加速度和速度，再根据平动参数分别补偿距离像偏移和回波相位的高次项，从而实现对空间目标回波的距离对齐和脉内走动的联合平动补偿。本算法不依赖于回波之间的相关性，且在距离对齐过程中不会引入距离偏移误差和高频相位误差。

1空间目标等效运动分析

首先，使用如图1所示的模型不失一般性地分析目标与雷达的相对运动，其中εo'η坐标系固定在目标上，η轴在t1时刻与雷达视线( Radar line-of-sight，RLOS)重合，a点和o'点分别为任意散射点和目标中心，XOY坐标系随RLOS转动。

两坐标系的关系为

式中:θ为RLOS的转动角度，Roi为ti时刻的雷达相对目标中心的距离。雷达相对目标上任意点a(εa，ηa)的距离可表示为

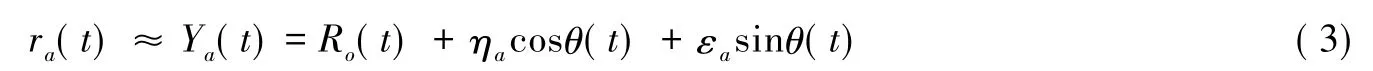
由式( 3)，可将ra( t)分解成等效转动和平动两个分量，即

式中目标中心o'到雷达的径向距离r ( t)和目标上任意点a等效转动引入的距离变化r( t)分别为

由于空间目标在空气十分稀薄的环境中运行，因此大气扰动对其运动的影响可忽略，且多数情况下

目标都遵循圆或椭圆轨道匀速运行。因此，从地面观测空间目标，其加速度α可忽略不计，平动分量可近似为二次函数［8，16］，则式( 5)可简化为

进一步分析目标平动分量对回波信号的影响，可假设发射信号为

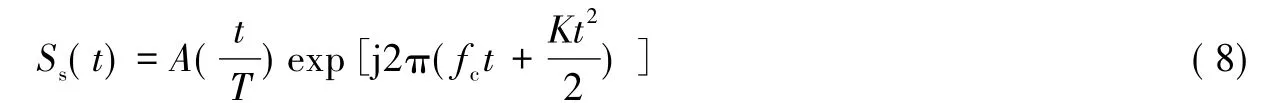
式中: A为信号包络，T为脉宽，fc为载频，K为调频斜率，t为快时间。那么任意散射点回波可表示为

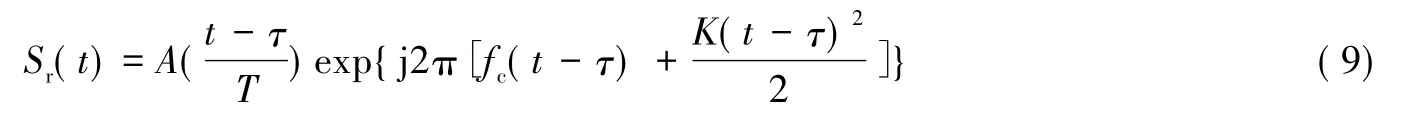
对式( 9)去斜得到的基带信号可表示为

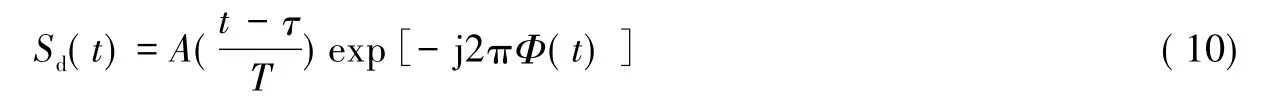
式中

由上述分析可知，空间目标的平动分量rT( t)为时间的二次函数，所以可用目标径向加速度α、径向速度v和起始距离Rc来表示，即

进一步将式( 12，14)代入式( 10)，则式( 10)中的幅度和相位分别表示为

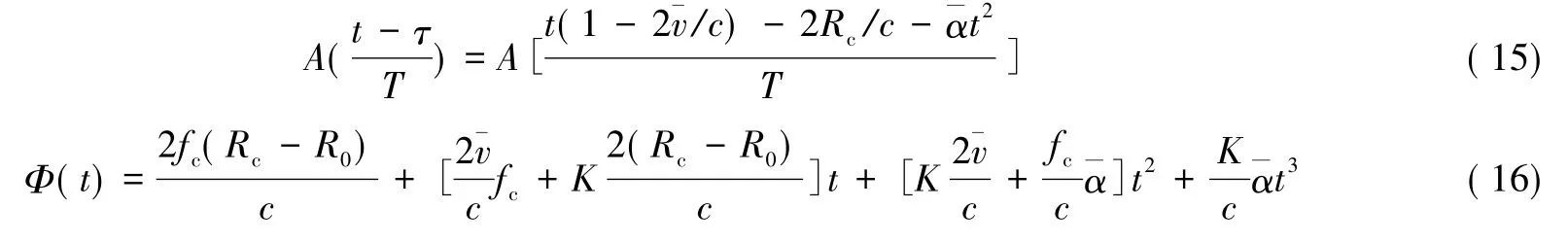
式中: c为光在真空中的飞行速度。由式( 16)可知，相位一次项包含了距离像的偏移信息，二次项和三次项则是由脉内走动引起的谱峰展宽和分裂。由此可见，距离像偏移和脉内走动均可用α和v表示，因此，估计出α和v就可以将距离像偏移和脉内走动问题一并解决。

2基于全局熵的联合运动补偿方法

上述相对运动中的线性分量称为距离走动，非线性分量称为距离弯曲，距离徙动是两分量的叠加，而目标的RMT就是所有散射点的距离徙动曲线的集合。本节拟利用目标RMT估计目标的平动参数即加速度和速度，并据此解决脉间和脉内联合运动补偿问题。

2．1基于RMT全局熵最小化的平动参数估计方法

假设有M个距离像pi( r+Δri)，i=0，1，…，M－1; r和Δri分别表示目标到雷达的径向距离和偏移量。用M个距离像的和包络定义平均距离像( Average range profile，ARP)，即

其中

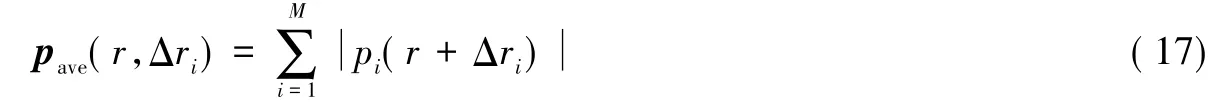
式中: PRF表示脉冲重复频率。那么，RMT的全局熵值可以定义为

其中Δr=［Δr1，Δr2，…，ΔrM］，S =∫rpave( r，Δr) dr。

对于同一段回波数据，距离对齐精度越高，其ERMT越小［12］。据此本文采用最小化ERMT作为距离对齐的准则，将平动参数v和α的估计问题归结为

即分别在闭区间［vmax，+vmax］和［－αmax，+αmax］内，期望估计出精确的速度v和加速度α，使得ERMT达到最小值。然而，在上述区间内对速度和加速度进行二维搜索十分复杂。考虑到v和α相互独立，因此双一维搜索是解决上述最优化问题的有效方法之一，即分别对v和α进行一维搜索让ERMT达到最小值。本文采用了文献［15］的搜索算法以加快算法收敛速度，该算法除了第一次迭代，每次迭代只要计算一个函数值，因此效率较高。

2．2距离对齐与脉内走动补偿算法

将速度和加速度的估计值ve和αe代入式( 14)，得到每一个距离像的偏移量估值Δrie为

由于Δrie不一定是距离单元的整数倍，若直接采用Δrie距离对齐将会引入较大的量化误差。因此，利用傅氏变换的时频移位对称性质对一维距离像pi( r)距离对齐，具体为

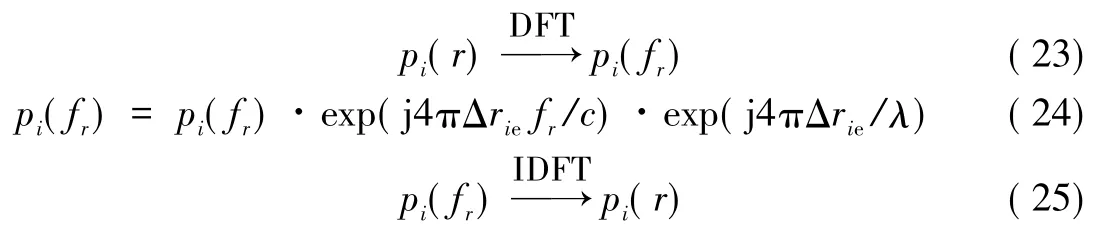
式中λ为波长，式( 24，25)分别表示线性相位项和距离偏移的相位补偿项。

另一方面，脉内走动造成的频谱展宽和分裂同样可以用平动参数估计值ve和αe来补偿。由第2．1节分析可知，为补偿式( 16)中的二次项和三次项，可令

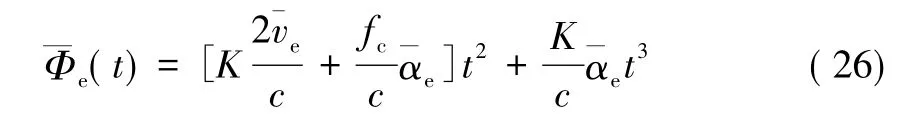
则脉内走动补偿后的回波信号可表示为

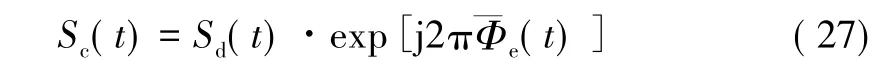
至此，距离像偏移和脉内走动根据平动参数均得到了补偿。上述算法的步骤流程图如图2所示。

3实验验证与分析

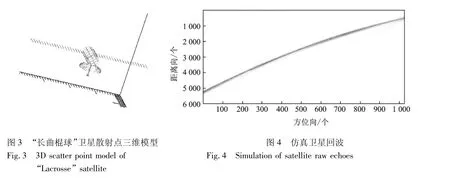
实验搜集了“长曲棍球”卫星的外形和尺寸，构建了如图3所示的该目标的3维模型( 960个标准散射点)。利用卫星工具包软件仿真目标过轨时的相对雷达位置和其自身的姿态，并据此构建了目标的标准散射点运动模型。图4为仿真该卫星运行到某个弧段时，对其遥测得到的回波。为了更加接近真实情况，在回波信号中加入了白噪声，使得脉压后的信噪比为3 dB。

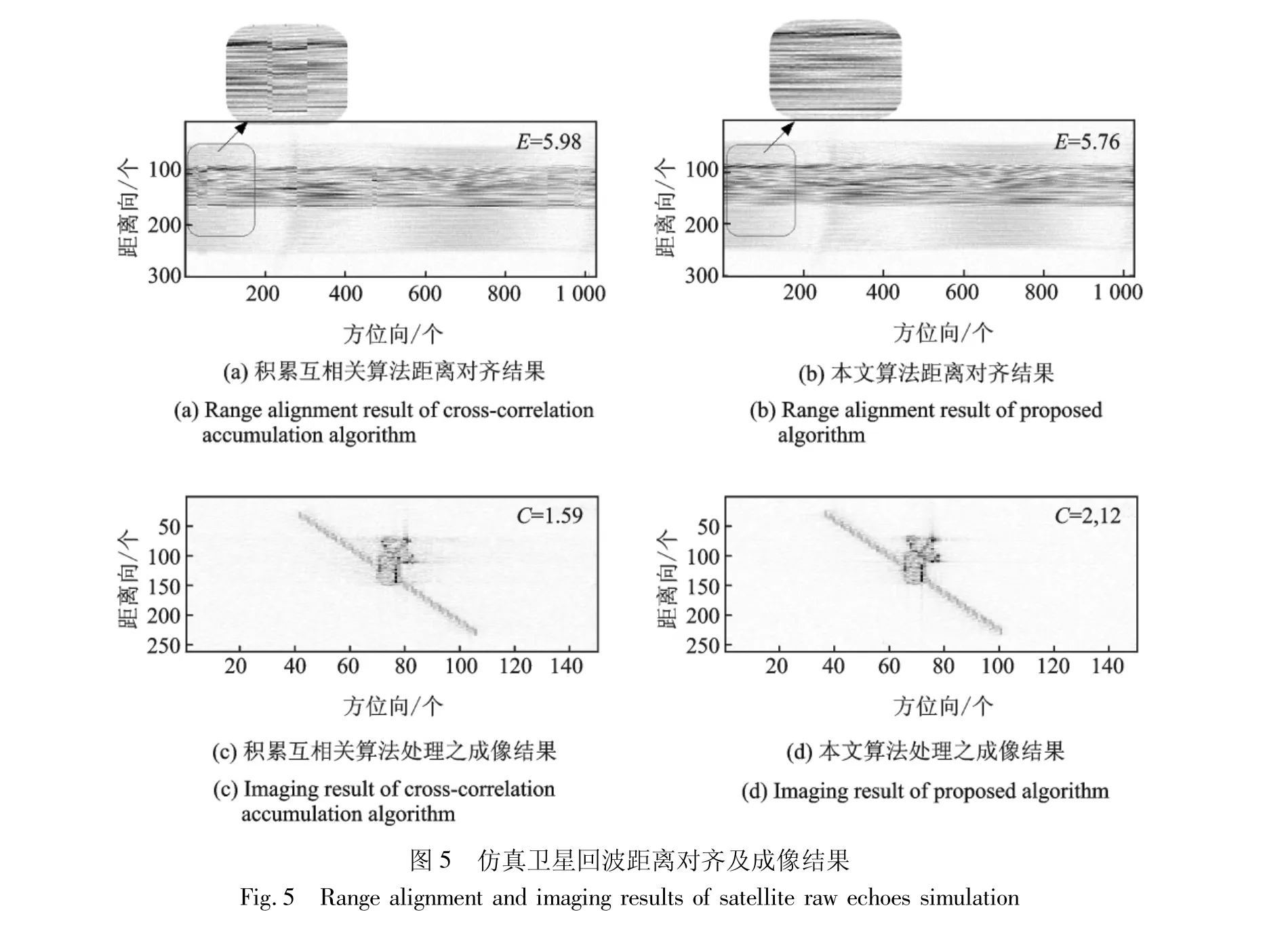
采用该仿真数据，分析本文算法的性能并与积累互相关距离对齐算法比较。首先，运用本文算法估计出目标径向速度和径向加速度分别为ve=231．452 9 m/s和αe=－69．775 4 m2/s;积累互相关算法的距离对齐结果如图5( a)所示，而基于上述运动参数的估值利用本文算法进行距离对齐的结果如图5( b)所示。需要说明的是，在运用前者时已经对回波距离向进行了4倍插值，而运用后者则不需要插值。通过比较图中的熵值(即ERMT)可知，后者的全局对齐精度更高。将图5( a，b)中的圈出部分放大，可从图像上看出后者的纹理更平滑，这进一步说明后者具有较高的局部对齐精度。在上述距离对齐的基础上，经过相位补偿最终成像的结果如图5( c，d)所示，后者图像对比度C更高，由此可知后者的聚焦效果更好。

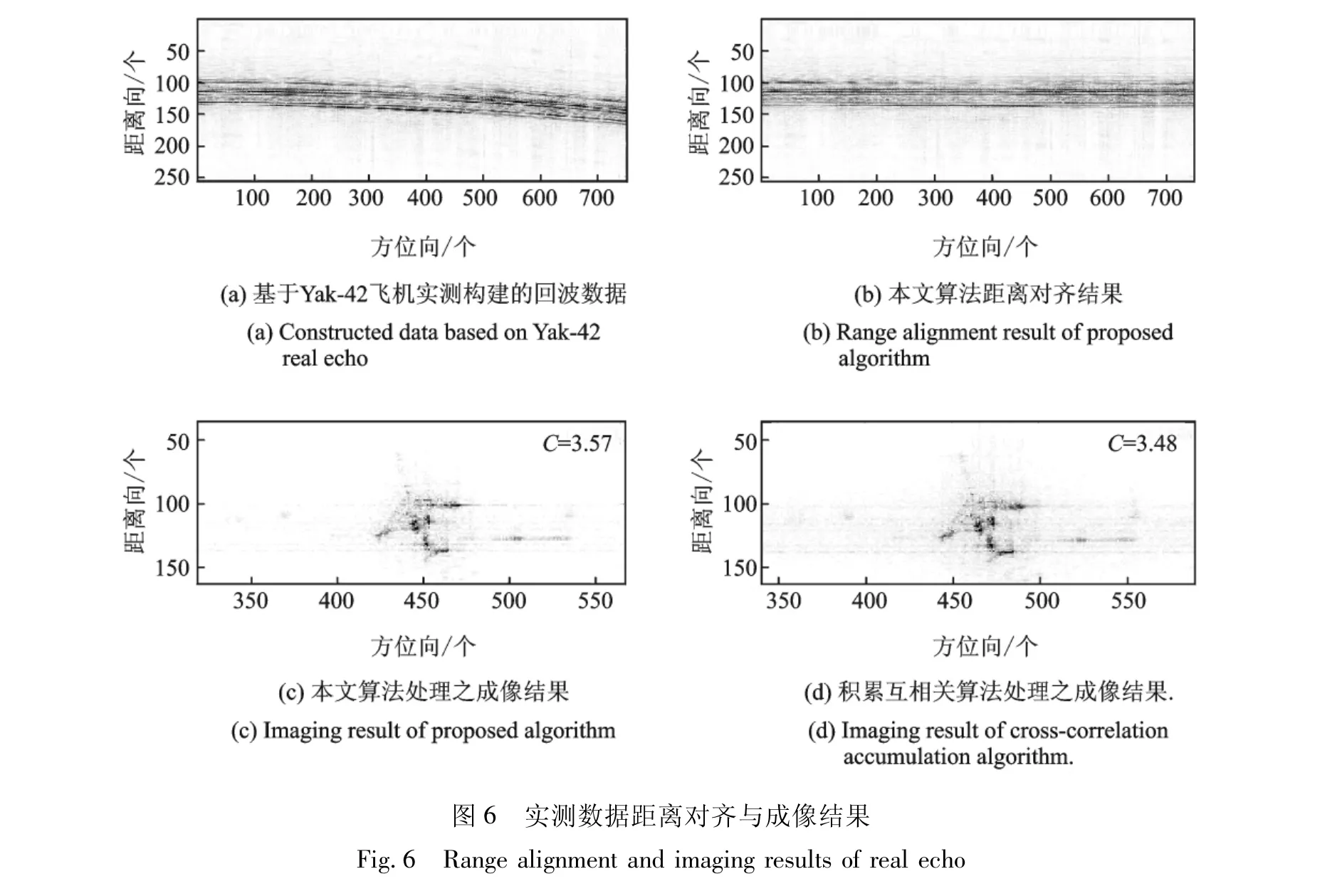
以下是基于实测数据的验证实验，基于Yak-42飞机实测回波构建了满足本文算法工作条件的数据，构建步骤为: ( 1)对Yak-42飞机实测数据使用全局最小熵算法距离对齐; ( 2)用二次函数扰动已对齐的距离像得到处理后的回波数据。图6积累互相关算法与本文算法的对比试验结果，比较图6( c，d)可知，由本文算法处理得到的图像质量较好。

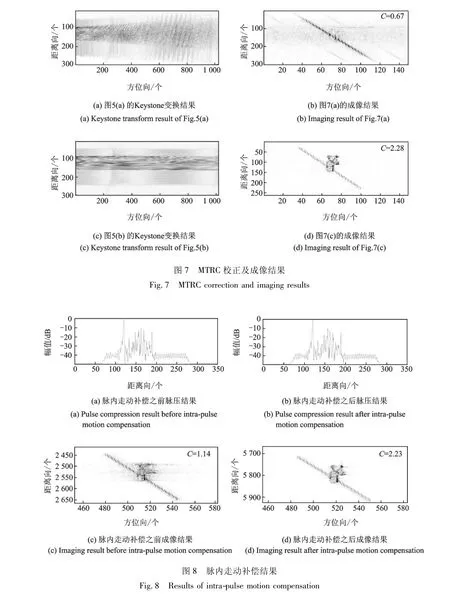
为实现高分辨率成像，需要采用大转角成像算法或者MTRC算法校正散射点的越分辨率单元走动。而运用上述两种方法的必要条件是需要回波具备完整和正确的相位历程。图5( a，b)经Keystone变换之后的结果分别如图7( a，c)所示，Keystone变换之后的成像结果分别如图7( b，d)所示。由于积累互相关算法在距离对齐过程引入了相位误差和距离偏移误差，不能满足Keystone变换的必要前提条件，使其失效，因此无法实现高分辨率成像。

固定雷达参数，脉内走动现象会随着目标径向速度增大而变得显著。如下实验中目标的径向速度为2 000 m/s，加速度为200 m/s2，其对成像的影响主要体现为目标点距离向的展宽，当然也会造成方位向散焦，结果如图8( a，c)所示。利用本文算法估计出的运动参数对回波校正和成像的结果如图8( b，d)所示，可见图像聚焦效果明显改善。

4 结束语

本文通过研究空间目标的运动特征，分析了目标等效运动模型与RMT的关系，并基于距离像全局熵值最小化原则，提出了一种距离对齐和脉内走动的联合平动补偿算法。实验结果表明，该算法准确性较高且不会引入相位误差和偏移误差，以后的工作将基于本文的研究成果，进一步研究空间目标大转角高分辨成像方法和方位向定标方法，最终提出空间目标的高分辨成像方案。