无人机中继链路传播损耗及性能分析

胡续俊 陈小敏 朱秋明,2 祝梦卿 陈 兵

(1.南京航空航天大学江苏省物联网与控制技术重点实验室，南京，211106；2.英国赫瑞瓦特大学工程与物理科学学院，爱丁堡，EH14 4AS)

引 言

无人机(Unmanned aerial vehicle, UAV)具有结构简单和造价低廉等优点，在通信、侦察、搜索和环境监测等众多领域得到了广泛应用。近年来，将无人机作为高空中继平台，用于提高地面移动自组织网络(Mobile ad-hoc network, MANET)的连通性、覆盖范围和服务质量的相关研究得到了国内外学者的广泛关注[1-7]。文献[1]研究了利用无人机中继平台提升网络的连通性，针对4种连通性准则的理论分析表明，单架无人机可提升约60%—240%的网络连通性。文献[2-3]研究了无人机中继的位置、指向及飞行路径的优化问题，其中文献[2]假设无人机采用多天线和波束成形技术，利用卡尔曼滤波法预测地面节点的移动位置，给出了一种基于最大信干比的无人机指向优化算法。文献[3]指出中继链路的遍历传输速率与无人机指向呈正弦函数关系，并据此提出了基于最小遍历传输速率门限的无人机数量及位置的动态规划算法。文献[1-3]均采用了随距离指数衰减的经验模型，该模型实现简单，但需要进行大量实测提供衰减指数，同时作者均仅考虑路径损耗因素，忽略了接收信号电平的随机起伏因素。文献[4-5]考虑阴影衰落和多径衰落的影响，其中文献[4]给出了单个无人机中继平台的有效统计覆盖区域。文献[5]提出一种采用编队飞行控制、基于分布式空时分组码的无人机协作网络系统，并通过飞行试验验证了该系统的可靠性。文献[6-7]重点考虑路径损耗叠加多径衰落的情况，分析单跳情况下中继传输方案及中断概率和遍历容量等系统性能指标。然而，大量地-空场景下的信道实测数据表明，阴影衰落普遍存在且不可忽略[8-10]，本文综合考虑机身姿态、天线特性、气候状况及阴影衰落等影响，建立了两跳中继链路的传播损耗模型。

无人机中继系统的布局、传输、优化和性能评估都与中继链路传播损耗的衰落特性密切相关。课题组曾对无人机单跳中继链路的多径阴影复合衰落模型进行研究，并指出其对无人机中继布局及优化的影响[4]。在此基础上，本文将重点针对两跳无人机中继系统，研究综合考虑飞机姿态、天线特性及气候状况的中继链路传播损耗预测方法。据此，进一步考虑多径及阴影复合衰落因素，推导获得中继系统的中断概率与误比特率的理论性能表达式，并利用仿真验证理论推导的正确性。

1 系统模型

1.1 无人机中继网络模型

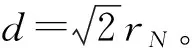
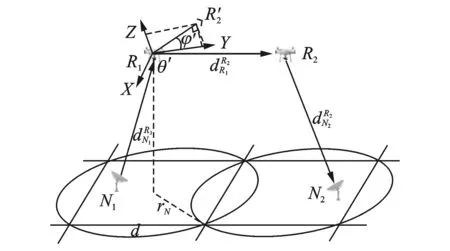
图1 无人机中继系统典型场景Fig.1 Dual-hop UAV relay system

(1)

式中

(2)

dR1R2在载体坐标系中的俯仰角θ′可表示为

(3)

1.2 中继链路传播损耗

对于任意相邻两个子网络中的地面节点N1和N2，若综合考虑天线增益、传播损耗和气候因素等，接收信号的功率可建模为

(4)

(5)

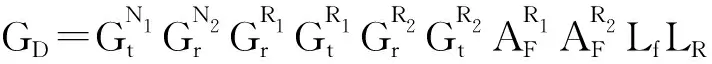
2 中继链路传播损耗分析

2.1 传播损耗均值

在无人机两跳中继链路中，接收信号的平均功率不仅与发射功率有关，还受到收发天线增益、转发增益、路径损耗和降雨损耗等因素的综合影响，对应传播损耗的均值可进一步表示为

(6)

(7)

式中：D表示地-空、空-空或空-地链路的传播距离；f表示载波频率；c表示光速。

降雨损耗的大小与雨滴的几何尺寸及其分布、降雨强度(或降雨率)、电波的极化方向、工作波长、接收地点的位置及海拔高度等诸多因素有关[12]。根据文献[13]的国际电信联盟无线通信组(Internationaltelecommunicationunion-radiocommunicationssector,ITU-R)雨衰分析方法，地-空、空-空或空-地链路的降雨损耗(记为A)可表示为

A=γRLE

(8)

式中：γR为衰减率，单位为dB/km；LE为穿越降雨区的等效路径长度。

鉴于无人机高度与姿态的实时变化，收发天线的增益计算比较复杂。为表示方便，将中继链路各天线的增益统一表示为

(9)

图2 中继链路相对传播损耗均值Fig.2 Relative mean of propagation loss of relay link

式中：D,η分别为天线的方向性系数和天线辐射效率；F(θ,φ)为归一化方向性函数，反映了天线在不同方向的场分布；φ,θ分别为方位角与俯仰角，二者可通过求解视距路径在载体坐标系下的方位角与俯仰角获得。

针对图1所示两跳无人机中继系统，假设不考虑雨衰情况，各无人机均采用归一化全向天线和归一化转发增益，信号覆盖区域边长10km，载波频率968MHz。为了观测地面节点与覆盖区域中心的距离dS以及无人机飞行高度h对整个中继链路传播损耗的影响，以h=1km,dS=0km情况下的传播损耗均值为参考值，图2给出了不同距离和飞行高度时相对参考值的额外损耗情况。由图2可以看出，(1)传播损耗均值随着dS与h的增加而增大；(2)当h=1km时，dS分别取最小值与最大值情况下的中继链路传播损耗均值相差约30dB，当h>7km时，dS的变化对传播损耗均值的影响极小；(3)当dS=0km时，h分别为1， 15km情况下的传播损耗均值相差约47dB，而当dS=6km时，h的变化对传播损耗均值的影响较小。

2.2 传播损耗衰落特性

无线电波在传播过程中会受到阴影衰落与多径衰落的影响，使得接收端信号的功率呈现随机的起伏。其中，阴影衰落指建筑物、植被等障碍物以及机身遮挡等因素导致接收信号功率的缓慢起伏。阴影衰落通常可建模为对数正态分布[14]，即

(10)

多径衰落是指信号在传播过程中由于受到复杂多样的传播环境影响，导致接收信号电平的快速起伏。目前，常用多径衰落模型包括瑞利、莱斯和Nakagami。其中，Nakagami分布比较灵活且已得到广泛应用，该分布可表示为[15]

(11)

式中：Γ(m)和Ω=E[x2]分别表示Gamma函数和多径衰落的平均功率。m≥0用于描述信道衰落的恶劣程度：当m=0.5和1时，该分布分别退化为单边高斯和瑞利分布；当m>1时对应莱斯分布。

无人机-无人机之间的链路为典型的空-空链路，由于始终存在视距路径且没有遮挡，信号的衰落因素可以近似忽略。因此，整个中继链路传播损耗的随机衰落可建模为空-地和地-空两段链路信号衰落的级联，则

(12)

式中：β1,γ1与β2,γ2分别对应地-空与空-地传播链路上的阴影衰落与多径衰落。根据随机变量的性质，级联后的多径阴影复合衰落幅度的概率密度函数可表示为

(13)

理论上将式(10，11)代入式(13)即可获得最终结果。然而，实际中该式不存在闭式解，从而对后续统计特性及系统性能闭式解推导造成很大困难。鉴于Gamma分布与对数正态分布比较相似，本文采用Gamma分布模型来建模阴影衰落[16]，则

-x/(Ωs/ms)

(14)

另外，可利用矩匹配方法计算获得二者参数的对应关系为

(15)

最后，将式(11，14)代入式(13)，可得到地-空与空-地链路多径阴影复合衰落包络的理论分布为

(16)

为了进一步获得级联后的中继链路信道衰落的等效概率分布，定义上述GK分布对应的矩生成函数为

(yi)dyii=1,2

(17)

级联后信道衰落分布对应的矩生成函数为

(18)

式中：G[·]表示Meijer-G函数。利用矩生成函数和概率密度函数的对应关系，可以最终推导获得空-地和地-空两段链路级联衰落α的包络理论分布为

(19)

式中：L-1[·]表示拉普拉斯逆变换。

在此基础上，定义地面节点N2接收信号的瞬时信噪比为

(20)

式中：N0=KT表示噪声功率谱密度，其中K,T分别表示波兹曼常数与等效噪声温度。结合随机变量变换性质，可得接收信号瞬时信噪比的概率分布为

(21)

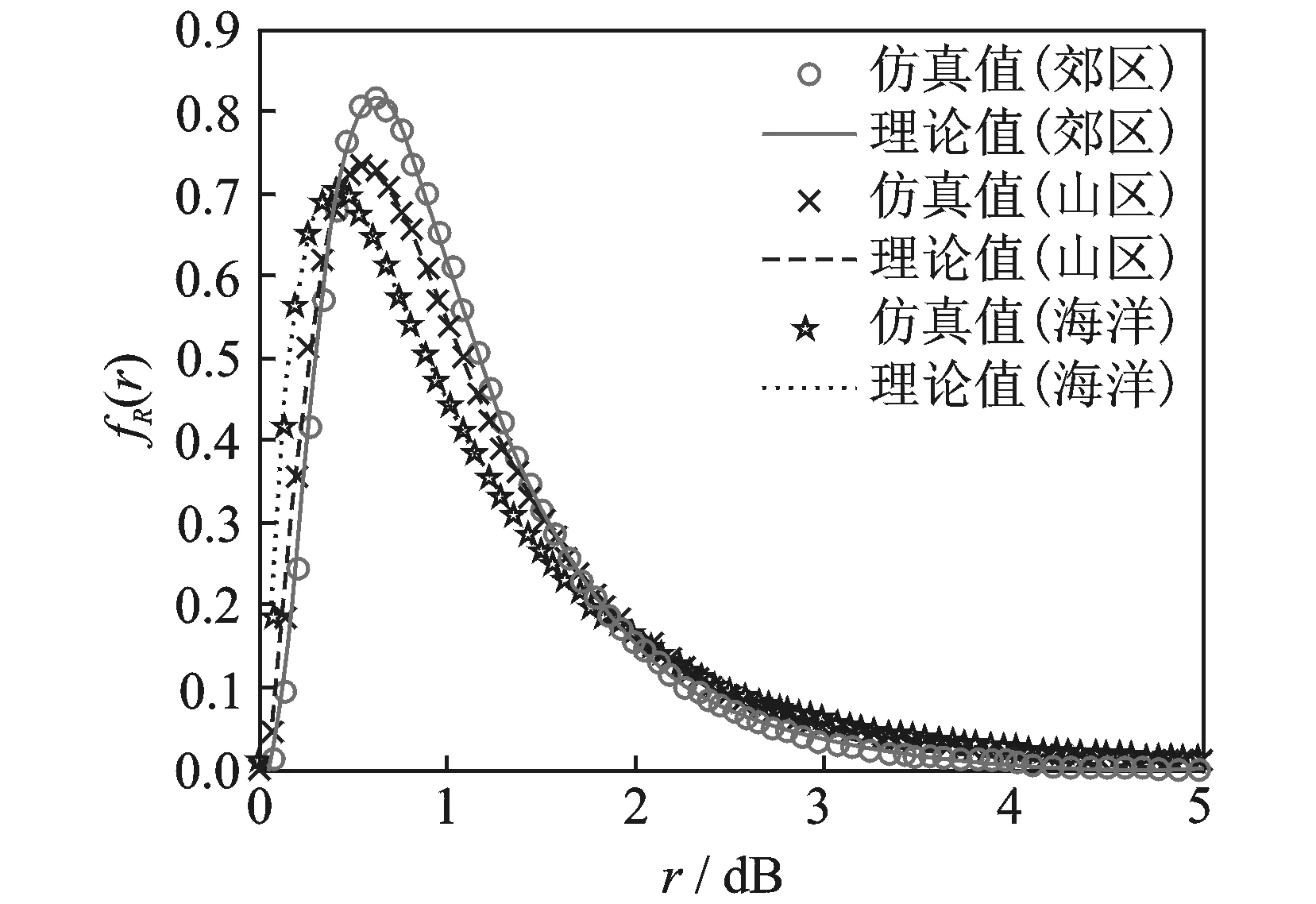
图3 不同场景瞬时信噪比分布Fig.3 Instantaneous SNR under different scenarios

(22)

为了验证本文推导获得的无人机两跳中继系统接收端瞬时信噪比分布的正确性，以3种典型场景为例，利用文献[17]提供的复合衰落随机生成方法对无人机中继链路接收端信噪比分布进行了统计验证。参考文献[8-10]的实测结果，令海洋、山区和郊区3个典型场景下的信道衰落参数为σx1=σx2，分别为4.2dB,3.5dB,2.6dB；m1=m2，分别为9.6,12.7,9.4。图3比较了接收端信号瞬时信噪比的统计结果(统计样点数106)及理论分布。从图3可以看到，各种场景下接收信号的瞬时信噪比统计结果与理论分布非常吻合，当位于郊区时，瞬时信噪比最集中，通信质量最好，而位于海洋时，通信质量最差。

2.3 衰落特性对系统性能的影响

中断概率定义为接收端瞬时信噪比低于接收机信噪比门限的概率。若地面节点N2接收到信号的信噪比低于最低信噪比门限r0，则信道中断。因此，中断概率为

(23)

将式(21)代入式(23)，可得无人机两跳中继系统的中断概率表达式为

(24)

误比特率是衡量无线通信系统性能的重要指标，无人机中继系统的平均误比特率(Averagebiterrorrate，ABER)定义为

(25)

式中：fR(r)表示无人机中继链路接收信号瞬时信噪比分布；Pe(r)表示信噪比为r时信号的误比特率。若发射信号采用BPSK调制，对应误比特率可表示为[18]

(26)

因此，利用式(21，25，26)，最终可推导两跳无人机中继系统的平均误比特率为

(27)

3 数值仿真与验证

为验证本文推导的无人机两跳中继系统的中断概率和平均误比特率(Average bit error rate, ABER)，假设信号覆盖区域边长10 km，发射功率1 W，载波频率968 MHz，无人机均采用归一化全向天线，转发增益也归一化且不考虑降雨因素。

图4 不同信噪比门限接收机中断概率与飞行高度关系Fig.4 Outage probability of receivers with different SNR thresholds at different altitudes

假设地面节点N2采用不同信噪比门限的接收机，对应门限余量分别为0，-3，-6 dB。图4给出了山区场景下不同接收机中断概率随无人机飞行高度的变化情况。从图4可以看到，不同接收机情况下的中断概率仿真结果与理论值吻合，(1)当h不变时，Δr0越大，Pout越大；当Δr0为定值时，随着h的增加，Pout逐渐增大；(2)当Pout<0.1或Pout>0.9时，随h的增加，Pout缓慢增大；(3)当0.1≤Pout≤0.9时，h的变化对Pout的影响很大，这是由于地面节点N2接收信号的瞬时信噪比主要集中于接收信号的平均信噪比附近，随着h的增加，地面节点N2接收信号的平均功率逐渐减小并接近信噪比门限值，从而导致Pout快速增大。

为了进一步观测不同场景下无人机飞行高度对中断概率的影响，图5分别对海洋、山区和郊区场景下的无人机中继系统进行仿真。

图5 不同场景中断概率与飞行高度关系Fig.5 Outage probability under different scenarios at different altitudes

从图5可以看到，3种场景下的中断概率仿真结果与理论值非常吻合： (1)当所处场景不变时，随着h的增加，Pout逐渐增大；(2)当无人机处于低空飞行时，该中继系统在郊区场景下的Pout最小，在海洋场景下的Pout最大，而h>10 km时，情况反之；(3)当0.1≤Pout≤0.9时，h的变化对于郊区场景Pout的影响最大，山区次之，海洋最小。结合图3可以看到，接收信号的瞬时信噪比相对集中于平均信噪比附近，而郊区场景下接收信号的瞬时信噪比最集中，故h变化所引起的接收信号平均信噪比变化对郊区场景Pout的影响最大。

图6 不同场景平均误比特率与飞行高度关系Fig.6 ABER under different scenarios at different altitudes

为了进一步观测系统性能，图6对典型场景下的平均误比特率进行了仿真。假设发射信号采用BPSK调制，无人机飞行高度为15 km时，接收信号信噪比为5 dB，且噪声功率固定，统计样点数为107。

从图6可以看到，3种场景下的接收信号平均误比特率仿真结果与理论值较吻合：(1)当场景固定时，随着h的增加，平均误比特率逐渐增大；当h不变时，该系统位于郊区场景下平均误比特率最大，山区次之，海洋最差；(2)当h<7 km时，平均误比特率低于0.001，无人机中继系统具有较好的性能。

4 结束语

无人机中继链路在通信过程中由于受到自身姿态、天气状况、通信距离以及无线衰落等因素影响，导致该链路通信质量下降。本文针对无人机两跳中继通信典型场景，建立了两跳中继链路的传播损耗模型，推导了接收端信号瞬时信噪比的概率分布，并由此获得了该系统平均误比特率的理论表达式。最后，通过计算机仿真验证了本文结论的正确性，并分析了通信距离、通信场景和飞行高度等因素对无人机两跳中继系统性能的影响，该结论对于无人机中继系统的规划和优化具有一定的参考价值。