国内外河流(网)非线性动力系统防灾分形理论研究综述
田福昌 ,苑希民 ,王秀杰 ,耿庆柱
(1.天津大学 水利工程仿真与安全国家重点实验室,天津 300072;2.天津大学 建筑工程学院,天津 300072;3.中水北方勘测设计研究有限责任公司,天津 300222)
河流(网)非线性动力系统发展一般遵循“相对稳定—混沌—无序—分形自组织—恢复相对稳定”的变化规律,演变过程表现出一定的混沌分形特征。混沌分形与自组织临界特性等理论的诞生与发展,为深入探知、充分认识、理解与诠释河流(网)非线性动力系统洪涝灾害演变发展特性及规律提供了一定的理论基础和科学支持,分形理论正由单学科向与人工智能、防洪减灾和河流动力学等多学科交叉性综合发展,因此,有必要归纳总结现阶段国内外河流(网)非线性动力系统防灾分形理论研究成果,展望未来发展前景与趋势,以期为分形学在防洪减灾领域的深入应用提供参考。本文将在河流(网)动力系统分形基本理论与常用分维数计算方法研究的基础上,重点阐述分形理论在长序列水文过程、洪水分期、河流形态演变、洪灾时序及频次规律、水文多尺度分形等方面的研究进展,分析现有研究存在的不足,提出河流(网)非线性动力系统防灾分形理论未来有待深入研究的主要方向。
在地理测绘工作中,通常来说,需要应用数据处理软件来对这些采集到的测绘数据进行编辑与处理,在处理过程中要先进行预处理,以此实现对测绘数据的拓扑建模。在地理信息系统中,能够将复杂的空间数据与属性进行紧密的结合,在对地理信息进行向量分析时,当某个拓扑数据正确,则可对待转化数据进行二次整合,使其成为地理信息系统能够自动识别的数据格式,进而使不同数据源之间得到有效融合,确保在后续的数据分析与处理以及在建立数学模型时能够打下坚实的基础。
矿石工业类型主要为蚀变岩型铜矿石、矽卡岩型铜矿石、蚀变岩型多金属矿石、矽卡岩型多金属矿石,按组构可划分为(细脉)浸染状矿石、块状矿石、条带状矿石、星点状矿石和角砾状矿石等,其中以(细脉)浸染状矿石最为常见。
1 河流(网)非线性动力系统防灾分形基本理论
1.1 基本理论概述1970年代,Mandelbrot[1]出版了著作《分形:形态,偶然性和维数》,标志着分形理论的正式诞生,随着《自然界的分形几何学》[2]的出版,分形理论已初步形成并逐渐成熟。分形几何学认为世界本质是非线性的,而分形理论则揭示了非线性系统中有序与无序的统一、确定性与随机性的统一,分形性是自然界普遍存在的基本属性[1]。
分形可以理解为一类及其零碎而复杂但有其自相似性或自仿射性的体系,具有“不规则的”、“破碎的”、“断裂的”和“分数的”等含义,分形理论的形成主要源于一些非光滑、不规则的集合和函数,比如 Canter集、Koch曲线、Julia集、Pianeo曲线、Sierpinski地毯和 Mandelbrot集等[3]。1986年,Man⁃delbrot[4]基于自相似性的考虑,给出了简单直观但并非精确的分形定义:设集合A⊂En,如果A的局部以某种方式与整体相似,则称A为分形集,认为局部可能在形态与组织结构等方面存在与整体相似的特性。然而至今还未有关于分形的严格定义,主要是将其看作具有以下性质的集合[5]:(1)具有精细的结构,即是在任意小的尺度之下,总存在复杂的细节;(2)具有复杂不规则性,它的整体和局部都不能用传统的几何语言来描述;(3)具有某种自相似性,这种自相似性不必是严格的,也可能是近似的或统计学意义上的;(4)在某种意义下的分形维数通常都大于它的拓扑维数;(5)在多数令人感兴趣的情形下,以非常简单的方法定义,或许以递归过程产生。
分形学作为非线性科学的重要分支,使人们能以新的观念和手段透过无序混乱现象和不规则形态,揭示隐藏在复杂现象背后的规律、局部和整体之前的本质关联,目前已被逐步应用于地貌学、统计学及河流动力学等众多学科[6]。
“双主体”是指教师是研究教材、划分知识点、创建课堂的主体,学生是利用在线课程自主学习、吸收知识的主体。网络课程针对细化的知识点配备教学视频、教学课件、在线自测题目、解题思路和解题答案等影音视频文档,改变了以往传统课堂的填鸭式教学模式,极大程度上调动了学生学习的积极性,提升了教学效率和教学质量。
河流(网)动力系统是具有明显分形特征的自然分形体,分形理论在河流动力系统研究中的应用主要包括长序列水文过程非线性特征识别及预测、洪水分期、河流形态演变、洪灾时序及频次分形、水文多尺度分形以及水流紊流结构、泥沙颗粒表面形貌、非均匀沙床面粗糙度及抗冲覆盖层表达等方面,其中前5个方面与河流非线性动力系统防灾领域密切相关,本文将重点论述。
(1)豪斯道夫(Hausdorff)维数。设A是度量空间(Rd,ρ)的任一有界子集S≥0,对于任意δ>0,定义:

2.5 水文多尺度分形分析研究研究内容主要包括水文序列多时空尺度的演变规律与特征分析、不同尺度间水文过程的衔接与转换、短中长期趋势分析与预测预报。自1990年代,由Gupta[91-92]正式提出水文尺度问题以来,水文尺度问题一直是水文科学领域研究的热点和难点。夏军[93]、Bloschl G.等[94]和Skop[95]给出了水文尺度与尺度问题的概念,探讨了水文尺度范围以及不同尺度水文过程模拟的复杂性,基本明确了水文尺度分析研究方向与方法论。随后,任立良[96]、刘贤赵等[97]和朱吉生等[98]众多学者对水文尺度问题进行了深入的探索与剖析。丁晶等[99]在水文尺度问题研究的基础上,首次提出水文多尺度分析的主要方法是分形理论、混沌理论、随机解集原理与小波理论。戚晓明等[100-101]从系统和多尺度水文模拟角度构建了水文尺度问题的研究框架,并建立水文多尺度仿真系统。刘建梅等[102]、钟晔等[103]和杨卫华等[104]学者讨论了水文尺度转换的复杂性及重点难点,认为分布式水文模拟与统计自相似性分析方法可作为水文尺度转换的另一途径。关于分形理论在水文多尺度分析预测中的应用,常福宣等[105-106]率先将分形标度理论应用于水文水资源领域,探讨了暴雨强度与大流域洪量随历时变化的标度性质以及年最大洪峰流量随区域变化的标度性质,阐述了暴雨洪水变化的尺度问题与相似性,初步证实分形理论在水文多尺度分析、转换及预测研究中的可行性与重要作用。张少文等[107]从水系河网结构和流域地形地貌及其演变、河床表面形态、降水时空分布、洪水时空变化、径流过程等方面,较为系统的论述了分形理论在水文水资源学科中的应用现状,并指出分形技术应用条件、适用范围、结果合理性与局限性分析、基于物理基础的成因机制论证等方面存在的不足。贺涛等[108]、刘起方等[109]基于时间序列的分形自仿射性,采用迭代函数系统、吸引子定理与拼贴定理提出了混沌时间序列的分形插值预测方法。王秋萍等[110]建立了长江大通站月平均径流量的新陈代谢分形插值预测模型。邱华旭等[111]采用累加和变换法构建了短时间序列分形预测模型。孔春芳等[112]基于Kol⁃mogorov熵与R/S方法建立了湖北省洪涝灾害成灾面积发展趋势分形混沌预测模型。同时,众多学者研究了混沌理论[113-114]、小波分析[115-117]与分布式水文模型[118-119]等方法在水文多尺度分析预测中的应用。
教师在教学过程中应注意启发学生学习如何思考问题、如何提出有价值的问题。例如,可根据社会上近期发生的引起重大关注的事件或学生提出的问题设定主题,先进行小组讨论,各小组推选代表上讲台讲述,鼓励学生提出各自的疑问和见解,引导他们多角度、多层面地思考问题。
2.1 长序列水文过程分形混沌特性研究主要是应用分形混沌理论识别长序列水文过程非线性特征,揭示水文时序复杂特性,判别水文过程变异动因及驱动因素,解决短期内水文序列的延长预测问题。最早由Hense等[9]应用混沌理论研究水文过程非线性特征,计算了Nauru岛长序列降雨过程关联维数,初步判定降雨序列可能存在低维混沌特性。随后Rodriguez-Iturbe等[10]与Wilcox等[11]人通过对周降雨、短期暴雨与冰山融雪径流序列进行非线性特性分析,表明了混沌现象存在的不确定性。Jayawaxdena等[12]和Sivakumar等[13-14]利用混沌理论分析了不同尺度下降雨和径流时间序列的非线性特征,均发现了混沌现象的存在。Radziejewski等[15]对波兰Warta河170年长序列日流量过程进行分形分析,采用盒计数变量法计算分形维数,综合分析了流量时序过程的分布式布朗运动特性(描述分形结构与赫斯特现象)。Vang等[16]、Movahed等[17]、Khatibi等[18]和 Tchiguirinskaia等[19]研究了长序列水文过程混沌现象、多重分形特性及时序延长预测方法,发现了混沌现象的普遍存在性,并表明季节因素和洪水位是影响径流序列混沌特性的重要因素。我国最早在由丁晶等[20]将分形混沌理论应用于水文学研究,初步探讨了洪水系统混沌特性识别与水文预测方法。随后王文均等[21]研究表明长江径流时间序列具有混沌特性,且流域面积越大混沌特性越明显。傅军等[22]对金沙江屏山站长序列日径流序列进行混沌特性识别研究,表明异常复杂的汛期径流过程是非线性动力系统演化结果,具有混沌动力系统特征。丁晶等[23]基于分形维数及短、长相关结构定量指标初步研究了年最大洪峰序列统计混乱性。刘德平[24]应用分形理论长江汉口站不同大洪水年份的水文过程形态特征及其差异性。赵永龙等[25]应用混沌理论探讨了不同嵌入空间下金沙江屏山站日流量时间序列关联维数的变化规律,揭示了水文动力系统复杂的运动规律,发现了不同程度的混沌现象。袁鹏等[26]发现多省市降雨水文现象均表现出混沌特性。李荣峰等[27]在混沌系统相空间重构基础上计算了月径流序列的嵌入维数和关联维数,进一步验证了水文过程混沌现象的存在。彭立等[28]采用R/S分析方法对岷江上游多年径流丰枯变化趋势进行了预测。王秀杰等[29-31]将小波分析、混沌理论与神经网络应用于黄河水沙变化周期及趋势分析、日径流回归预测预报、日含沙量时间序列的混沌识别与预测等研究,建立了径流与含沙量趋势分析及预测模型。徐国宾等[32]研究了黄河不同河型径流量、宽深比和输沙量等时间序列非线性特征,表明不同河型具有不同强度的混沌特性且游荡型河道混沌特性最强。
1.2 常用分形维数分形体最主要的特征是具有自相似性的分形结构,在无标度区间内表现为局部与整体的自相似性。分形维数作为分形体定量描述的重要参数,能够定量表达分形体结构的自相似程度、不规则程度或破碎程度。为从不同角度反映不同分形体的属性与特征,目前已发展形成多种分形维数概念,包括豪斯道夫维数、盒维数、相似维数、容量维数、关联维数、信息维数、谱维数和广义维数等[7-8],本文重点给出以下几种在河流(网)非线性动力系统防灾领域应用较为广泛的分形维数定义。
(3)关联维数。对于一组实测时间序列,x1,x2,x3,…,xi,…,其中xi对应着i时刻的值,若该序列的时间间隔为Δt,则 y1=x1,x2,…,xm;y2=x2,x3,…,xm+1,…;yN=xN,xN+1,…,xN+m-1构成了延滞时间为Δt的m维嵌入空间中的N个点。任给半径为ε的小球,则距离小于ε的点对在所有点对(N2个点对)中所占的比例为:
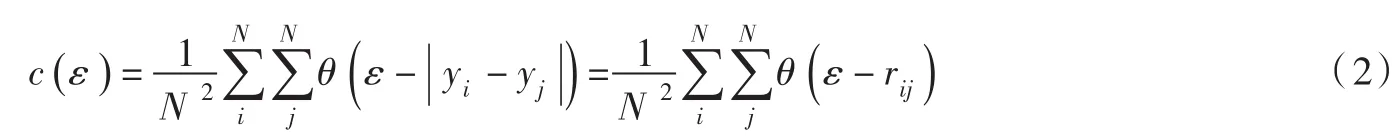
(4)信息维数。若用尺度为δ的盒子去覆盖整个分形集,对应于第i个盒子的几率为Pi,信息维数D的定义为:
国内外关于河流(网)非线性动力系统防灾分形理论研究已取得较为突出的成果,尤其表现在长序列水文过程分形混沌特性、洪水分期分形、河流形态演变分形、洪灾时序及频次分形等方面,基本反映了水文过程、河流演变与洪涝灾害系统的分形演化规律及本质特征。笔者认为现有河流动力系统防洪减灾分形理论研究方向及内容尚存在些许不足,比如:水沙时序的混沌分形研究多是针对径流量与含沙量等指标,鲜有学者系统研究输沙率、来沙系数与泥沙冲淤量的非线性分形特征、变化发展趋势预测及分形信息维物理机制;河流形态及河势演变分形研究多是分析横断面、纵剖面与平面形态的基本分形特征,缺少“横-纵-平”多维形态分形演变关联关系及河势特征复合参数(比如河相系数、滩槽宽度及边界线长度、弯曲度等)分维特征的系统研究成果,且少有学者研究水沙变异条件与河道防洪工程耦合作用对河势演变分形结构的调制机制;缺乏对洪涝灾害分形分维动力机制与灾变演化机理及预测方法的深层次研究;水文多尺度时空演变规律及尺度转换仍是亟需攻克的前沿理论难题;分形预测精准度与预见期有待进一步提高等等。

2 国内外研究动态与现状
当时她先是演唱一首歌,我就悄悄地躲在后台。等她刚刚唱到中间,有一个点是在间奏的时候,我就忽然走出去,拿着奖杯,她一转身看到我,在台上转身就走,我就只好在台上追着她,她就绕着那个舞台一直走,一直不肯接受我给她的这个奖。我跟在她后面,嘴里一直讲,不要这样,Teresa,不要这样,很难看啊……后来她终于拿了这个奖,也没有跟我握手,也没有说谢谢,就转身走掉了。气得我回去就骂林建岳,她根本就不知道是我要给她颁奖!
(2)盒维数。设A是n维欧式空间的一个子集,对每一个δ>0,用表示覆盖A的半径为δ的闭球的最少个数,若存在,则称此极限为集A的盒维数,记为S,那么即覆盖A的闭球数幂律。
2.2 洪水分期分形理论应用研究随着分形理论的崛起与快速发展,分形维数方法已被广大科研工作者应用于洪水分期研究领域,主要是应用分形维数理论识别洪峰时序散点的分维特征,更为客观地确定洪水汛期时段组成,揭示流域雨洪季节特性和分期规律,为流域产汇流机制研究、水资源优化配置与利用、水库运行调控和防汛指挥决策等提供科学支持。Turcotte等[33]以美国10条河流不同基准站历史洪水记录为依据,分析了洪峰流量与时间变量之间的幂律关系,发现两者之间具有良好的标度不变(分形)特性,论证了分形幂律统计关系在洪水频率估算中应用的可行性。Mazzarella等[34]应用康托尔(Cantor)统计法与排序(rank-ordering)统计法分析了意大利Po River上游大洪水发生时间的变化规律,证明了洪水事件发生的标度不变性及其在洪灾预测评估与防洪减灾领域的重要作用。Mal⁃amud等[35]以美国地质调查局的6处水文站为研究对象,综合考虑年最大洪水与局部持续(partial-dura⁃tion,年度多次大洪水过程)洪水序列,研究了洪水频率统计的幂律特性,认为局部持续洪水序列中洪峰流量与重现期存在较好的幂律关系,而基于年最大洪水序列的洪水频率估算结果偏差较大,因此提出了极端洪水变换方法以修正概率误差。Alipour等[36]以美国两个相邻水资源区的大量汇水流域为分析对象,考虑将季节因素作为洪水形成主要条件,划分夏冬两季洪水过程并进行分形特性研究,认为季节性洪水分形分析方法有助于提高洪水量级估算精度、辨识区域性洪水形成机制、揭示洪水事件潜藏的详细特性信息。我国自1990年代起,侯玉等[37]首次分析了洪峰散点序列的自相似性与分形特征,提出应用分形理论确定洪水分期的方法,并基于雅垄江小得石站洪水分期成果初步验证了该方法的可行性与可靠性。随后,方崇惠等[38-39]在水文现象分形特性分析基础上,提出了时间尺度容量维和空间尺度相似维计算方法,并将其应用于漳河水库汛期分期的划分研究,对比分析得出分形维数法具有客观、定量与计算简便快捷等特点。董前进等[40]利用传统统计学法和动态分维数法研究了三峡水库汛期洪水分期。韩杰等[41]应用分数阶积分估算维数法计算了金沙江上游石鼓站洪水分期,并结合传统洪水分析方法论证了分形维数法的客观性和准确性。金保明等[42]研究了容量维数绝对度量法在汛期分期中的应用,并将其应用于闽江上游建阳市汛期分期分析,表明分形分析方法能够揭示暴雨洪水季节特性和分期规律。艾学山等[43-47]众多学者基于分形理论分别研究了不同流域和水库的洪水分期识别,综合对比分析数理统计、成因分析、系统聚类、分形维数与圆形分布等方法的计算结果,进一步论证了分形理论在洪水分期划分应用中的可靠性。张礼兵等[48]将Hausdorff维数分形方法应用于梅山水库入库径流干旱预警时段的划分,优化确定了不同预警时期的旱限水位。
2.3 河流形态演变分形研究主要是应用分形几何学理论与3S技术研究河流平面、横剖面、纵剖面和床面等多维度形态演变分形特征,探讨形态分形与流域洪水特性、河床边界的内在关联,揭示河流分形与最小能耗、动力系统演变、自组织调整之间的相关规律,为河型转化判别、洪凌灾害防治提供一定理论支撑。分形理论创始人Mandelbrot[1]最早将分形学引入地理水文学领域,通过河流分形特性探讨了河流长度与流域面积之间的相关关系,随后众多学者应用分形理论研究了河流形态及其演变特征[49-50]。比如 Feder等[51]基于霍顿定律推导了主河道分维计算公式。Robert[52]研究了冲积河流沉积动力过程的分形特征,推求了能够反映河床剖面粗糙度分形特征的标度指数。Gupta等[53]分析了河流网络的自相似性并给出了流域坡降与其几何特征的相关关系。Tarboton等[54]建立了河流地貌演化与河网密度的联系,分析了尺度变化对分形维数的影响。Nikora等[55]计算了Moldavia境内46个地貌齐性河段河流中心线分形维数,认为其可为表征河流平面形态内部结构特点的有效参量。Nykanen等[56]提出了辫状河流平面形态自相似性和自仿射性计算方法,并应用自组织临界理论诠释了河流演变过程。Bartolo等[57]采用盒维数法计算了意大利南部6个河网的广义分形维数,揭示了河网系统的多重分形结构。我国于1990年代开始,张矿[58]通过分析长江形态的分形特性,表明分形维数可以客观反映河流形态的复杂程度。汪富泉等[59-61]论述了分形混沌理论与系统思想的辩证关系,探讨了河流(网)系统分形结构形成机制,应用量规维数法研究了蜿蜒河流分形特征并揭示了河流平面形态演变规律。金德生等[62]应用粗视化方法分析了黄河下游及长江中下游河段河床深泓纵剖面分形特征。刘怀湘等[63]运用Horton定律定量分析了羽状河网、叶状河网和枝状河网等三种典型河网形态的平均Horton比和流域外型参数。冯平等[64]基于分形理论及河系定律计算了海河水系河长和河网分维数。冯金良等[65]通过计算海河流域水系盒维数,探讨了水系分维合并原理与物理意义,尝试建立了流域径流模数与水系分维的关联关系。王世俊等[66]基于多历史时期珠江河网地图及遥感影像数据,从河流发育与人类活动等多角度揭示了珠江河网的分形机理。白玉川等[67]分析了蜿蜒河流平面形态分形盒维数,并对大型河流不规则程度和弯曲度进行了分形描述。王卫红等[68]利用分形理论探讨了基于最小能耗率的河流演变机理,推导了河流能耗与河型判别的分形公式。周银军等[69-72]充分结合河流动力学与分形理论,探讨了河床表面分形特征及分维数变化与河段横断面、纵剖面、平面形态冲淤调整之间的关系。刘亚博[8]构建了河道非恒定流-分形数学模型,利用分形标度研究了河道洪水非恒定流流动特性与横纵剖面分形机制。
2.4 洪灾时序及频次分形研究国内外学者针对分形理论在洪涝灾害领域中的应用,开展了大量的创新性研究工作,取得较为丰富的研究成果。主要是应用分形混沌理论深入认识洪灾系统特性及灾害规律,研究洪涝灾害系统时序分形特征,探知分形特征蕴含的灾害发生规律和自组织水平,构建灾害分形预测模型,预测洪涝灾害发生概率及灾害影响发展趋势。Kirkby等[73]应用分形理论研究了水文气象长序列记录数据表现出的分形特征及其趋势延伸意义。Scheidegger[74]提出了自然灾害领域的混沌、自组织与分形理论,通过河流水文洪水频率与滑坡等方面论证了灾害发展过程中的分形幂律关系。Gupta等[75]总结了河网洪水非线性地球物理学理论主要研究成果,探讨了河流网络分形结构的自相似性及时空幂律统计关系,指明其在地球气候显著变暖背景下的洪水预测、水资源与水能均衡分配等领域的实践意义。Zon-Yee等[76]从分形维数(盒维数和关联维数)角度分析了Chenyulan Creek流域滑坡面积与临近两次滑坡灾害发生距离的分布特征,表明该流域坡度易变不稳定且滑坡灾害频次具有逐渐增加趋势。Ahmadi等[77]基于分形幂律函数性质分析了伊朗Dez流域的洪水序列特征并探讨了设计洪水可能性分布过程。Ichim等[78]基于局部二元图(Local Binary Patterns)、方向梯度直方图(Histogram of Oriented Gradients)和分形维数(Fractal Dimension)等融合理论,通过对遥感影像进行纹理识别与描述,建立了洪水淹没区动态监测与评估方法,以精准确定洪水等级及淹没风险。我国自1990年代开始,周寅康等[79-80]分析了分形论在地震和洪涝灾害中的应用成果,展望了分形理论在自然灾害研究领域的发展前景与亟待深入探讨的问题,并研究了淮河流域洪涝变化序列的分形特征以及洪涝序列信息维数与发生频度的相关关系。李祚泳等[81]初步探索了我国自然灾害(旱、涝、飓风和地震)发生时序的分形特征,认为无标度区跨度及相应分形维数代表了自然灾害自组织程度。杨思全等[82]基于混沌理论研究了天山黄水沟突发性洪水灾害非线性特征及动力机制。朱晓华等[83-84]系统分析了我国不同地区不同流域旱涝灾害分形结构,建立了流域水系维数与洪涝灾害分维之间的相关关系,研究了我国自然灾害客观存在的自组织临界特性,揭示了自然灾害灾情标度与频度之间的分形幂律关系。赵晶等[85]应用分形理论研究了我国1950—1997年洪涝灾害农田成灾面积分形特征,并应用R/S分析法对其变化趋势进行预测。马宗伟等[86]以长江中下游为例探讨了河流形态分维特征及其与洪水发生概率的相关关系,研究认为洪水发生可能性与河道分维数成正相关、与河网分维数成负相关。谢云霞等[87]提出以能够反映评价指标复杂程度的分维数作为指标权重的城市洪涝易损性评价方法,并基于集对分析理论研究构建了分形模糊集对评价模型。另外,王良健等[88]、倪化勇等[89]和丁贤法等[90]众多学者相继研究了不同地区洪涝灾害时间序列分形特征及发展趋势。
3 研究中存在的不足
他预感到,在情感上有着某种相似孤独感的伍亦苒同样也在期待,期待在故事的中段因为情节激荡而生发出的高潮。
4 研究前景展望
4.1 流域多尺度洪灾分维动力机制研究受暴雨中心分布、洪水过程、水系特征及防洪能力、区域地形地貌、社会经济发展规划等多方面因素影响,流域洪涝灾害呈现出成因复杂性、时空多变性和损失严重性等特点,且已被众多学者证实具有一定的自相似分形特性。然而关于洪涝灾害分形结构形成及演变的动力机制尚未得到有效揭示,今后需高度融合灾害学、分形学、地形学、河流动力学等多学科理论,研究洪灾自相似性、自仿射性胖分形及多重分形特征,从暴雨洪水、河流水系、地质地形、历史洪涝灾害等多角度探索多时空尺度下流域洪灾发生发展规律及机理、分形特征、混沌演化过程与预测预报方法,建立多尺度时序洪灾分形动力模型,形成完整的流域多尺度洪灾分维动力学理论体系。
4.2 河型转化分维判别标准研究河型转化是水沙条件与河床边界条件共同作用而产生的一种突变结果,影响因素多、转化机理复杂、判别依据难以准确定量化,河型转化判别标准一直是河流动力学领域亟待攻克的研究难题。当前已有学者通过河流比降-平滩流量关系、单位水流功率、游荡摆动强度指标、河流相应切应力、系统协调发展度、耗散结构理论和超熵产生等方面探讨了不同河型判别公式及稳定性条件,多表现出一定的潜在分形幂律关系,然而这一规律却并未得到深入揭示与表达,未来应用分形学理论深入研究不同河型分形特征、分维演变规律及综合判别标准,有望进一步丰富河型转化及稳定性判别理论。
4.3 河流演变复合参数分形特征与物理机制研究河流演变影响因素主要包括来水来沙条件与河床形态两个方面,综合体现河流演变特征的复合参数能够更加有效地揭示系统发展变化驱动机理。因此,应用小波消噪改进的饱和关联维法和重标极差分析法R/S(Rescaled range analysis)研究输沙率、来沙系数、泥沙冲淤量等长序列水沙冲淤复合参量演变趋势及非线性分形特征,分析挖掘各参量分形信息维物理机制及相互关联特性,建立水沙变异条件下河流冲淤演变的小波消噪与分形神经网络智能预测模型,具有重要研究与实践价值。基于分形信息维与3S(GPS/GIS/RS)技术,研究“横-纵-平”多维剖面、河相系数、滩槽差、滩槽平面与宽度关系、弯曲度、滩槽边界线长度等河势演变复合参量分维数物理机制与分形特征时空变异规律,探讨“人类-自然-社会”耦合作用对河势演变格局及其分形结构的调制机制,将是水利信息化与智能化深度融合下的又一重要研究方向。
4.4 堤防灾变系统演化分形混沌理论研究现有堤防险情灾变机理研究成果,多是关于单一险情破坏机理及失稳临界条件分析与预测,而针对堤防多类别险情联动(如:冲蚀-渗流-坍塌-溃决)诱发机理、破坏特点及险情演化过程的研究成果甚少。笔者认为应用分形学、混沌学、耗散结构、最小熵产生与最小能耗原理、突变论、自组织临界理论等非线性系统科学,结合河流动力学、灾害学与人工智能学理论研究河流堤防系统险情灾害的孕育、发生、演化与传播规律以及灾害影响评估与预测预报方法,将是堤防灾变系统演化分形混沌理论深入发展的重要趋势。比如:研究高纬度河段凌汛期堤防险工段分形诊断方法及时空动态演化智能预测模型,揭示水沙-工程联合作用下堤防险情成因、过程、特征及冲塌崩岸演化机理,探讨堤防多类别险情演化机理的混沌分形、耗散结构与自组织临界理论合理性诠释,为流域河网系统防灾智能化分析调控、智慧建设与管理、健康协调发展等提供科学支持。
第一,从有限的差等性责任到普遍的平等性责任。传统社会差序性的身份设定衍生了差等性的责任。在家庭中,家长或族长、男性、长辈拥有更多的权利,而女性、晚辈需承担更多的责任,且这些责任是不以对等的权利为前提的单向性道德义务。同时,因农耕文明的生活方式、社会公共交往空间的狭小和与来自陌生地域、异己文化的陌生人交往的偶在性决定了传统社会的人们基本上都生活在以血缘关系为基础的小型熟人共同体内,人们生于斯,长于斯,老于斯,生活半径小,生活内容简单,与其交往互动的他者相对稳定,一般而言,熟人共同体就是人们的道德责任所抵达的边界。因此,传统社会的道德责任在时间、空间和他者的意义上都是有限的。
4.5 水文多尺度智能分形与决策支持研究由于水文现象具有空间异质性和时空变异性特点,水文学理论与模型具有高度的尺度特性,尺度分析与尺度转换仍然是未来长期亟待解决的难题,主要包括不同时空尺度下水循环物理过程的变化规律及特征,以及微观、中观、宏观等不同尺度间水文过程的衔接与转换,有望通过分形理论、混沌理论、小波分析、协同理论、3S技术和分布式水文模型等技术理论的相互渗透与耦合得以解决。关于变化环境下水文条件(如暴雨、洪水条件)的预测,有望进一步深入探索水文现象背后隐藏的非线性科学奥秘,揭示水文现象成因及其产生的非线性机制,结合分形混沌与小波分析、神经网络等方法实现短中长期不同时间尺度下水文过程及洪涝灾害的自动化、智能化和高精准预测。结合实际防洪减灾应用需求,拓宽水文多尺度分形研究服务领域与应用范畴,集成于防汛抗旱指挥系统或洪水预报等业务支撑平台将是水利信息化与智能化发展的趋势之一,可为河流非线性动力系统防灾指挥提供决策支持。
4.6 水利智能分形复合理论的提出与发展目前,人工智能与分形理论已被初步应用于河床及河型演变研究领域,但尚未在河势演变及水沙灾害领域得到较为深入的研究与应用,学科交叉融合度不高、创新性略有不足。随着人工智能技术理论的发展与推广应用,智能水利工程学必将迎来崭新的发展势头,在逐步深入揭示水利科学发展规律的过程中,实现人工智能方法(遗传算法、人工神经网络、小波分析、灰色系统理论、量子退火优化算法等)及其优化理论、混沌分形与自组织临界特性理论、协同论、突变论、耗散结构等与水利工程学科的深度融合与耦合创新,形成涵盖水沙冲淤、河势演变、河流险情灾情演化及预测、水文多尺度等多领域的水利智能分形复合理论,该复合理论的主要特点是多学科理论、多技术方法的相互交叉与融合应用,充分体现了人工智能与非线性科学理论探索揭示水利科学多领域发展规律的优势,利于推进河流(网)非线性动力系统防灾指挥决策的智能化。

