两变量洪水结构荷载重现期与联合设计值研究

刘章君，郭生练，许新发，成静清，温天福，尹家波

（1.江西省水利科学研究院，江西 南昌 330029；2.武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072）

1 研究背景

洪水重现期与设计值的分析计算是水库防洪安全设计及风险分析的关键问题[1］。单变量情况下，重现期和设计值存在唯一的对应关系，计算方法清晰简单。在两变量情况下，由于涉及到洪峰、洪量的组合，因而重现期的定义和联合设计值的计算都要比单变量情形复杂得多，近年来相关的研究受到了国内外水文学者的高度关注[2-4］。

根据两变量框架下危险区域的划分方式不同，目前对两变量洪水重现期的定义也相应有很多种。“或”（“OR”）和“且”（“AND”）重现期是目前使用最广泛的两种定义方法，它们均根据某一特定洪峰、洪量联合设计值定义危险区域，大量研究表明，在安全与危险事件的判定上两者都存在着较大局限性[5-9］。为了解决上述问题，Salvadori等[5］根据联合概率等值线定义危险区域，基于Kendall函数提出了两变量洪水Kendall重现期，认为只有当洪峰、洪量联合概率值超过了设定的阈值时才是危险事件。Kendall重现期使得洪峰、洪量联合概率等值线上的任意一点都具有相同的危险区域，对安全事件与危险事件的判定更加合理[10-12］。此外，考虑到对于洪水这种对于越大越不利型变量，理论上安全区域应该是有界的。针对Kendall重现期安全区域无界的问题，Salvadori等[13］在此基础上又提出了两变量洪水生存Kendall重现期，使得两变量洪水重现期定义更加严谨。

事实上，就水库防洪安全而言，最重要的因素是坝前最高水位，真正的危险事件应该是坝前最高水位超过某一指定高程[14］。前述4种两变量重现期所判定的危险事件和表征的水库大坝水文失事情景都可能不符合实际情况。因此，有些学者更加突出强调水文荷载（如洪峰、洪量）与水工结构的交互作用，提出了基于水工结构安全的两变量洪水重现期，并依此进行相关的洪水联合设计和风险评估[15-17］。国内外相关研究仍处于起步阶段，尚未形成统一方法构架，且大多数都进行了一定的概化或简化处理，例如将入库洪水过程形状概化为三角形、水库调洪演算简化为线性水库模型或自由泄流模型等。目前对于具有实际洪水过程线形状和复杂调洪规则的情形在国内外尚未见诸文献报道，亟待深入研究。

本文将针对具有实际洪水过程线形状和复杂调洪规则的情形，以超过坝前最高水位的频率来度量防洪安全设计标准，通过坝前最高水位等值线划分危险区域，开展两变量洪水结构荷载重现期（TSL）与最可能联合设计值研究。以清江流域隔河岩水库为例进行应用，并与常用的“OR”重现期（TOR）、“AND”重现期（TAND）、Kendall重现期（TK）和生存Kendall重现期（TSK）等4种两变量重现期最可能联合设计值进行比较，以期为水库防洪安全设计和风险分析提供更加科学合理的依据。

2 两变量洪水结构荷载重现期计算方法

2.1 基于Copula函数的洪水峰量联合分布假设Q、W分别表示年最大洪峰流量和时段洪量，对应的设计值分别为q、w，其边缘分布分别为由Sklar定理知，Q和W的联合分布函数可以用一个二维 Copula函数 C表示[18-19］：

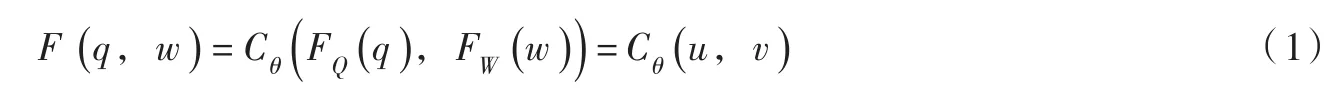
式中：F（q，w）为Q和W的联合分布函数；θ为Copula函数的参数。

一般而言，洪水峰、量之间存在较强的正相关性，通常采用Gumbel-Hougaard Copula函数来构造二者的联合分布，其表达式如下[20-22］：

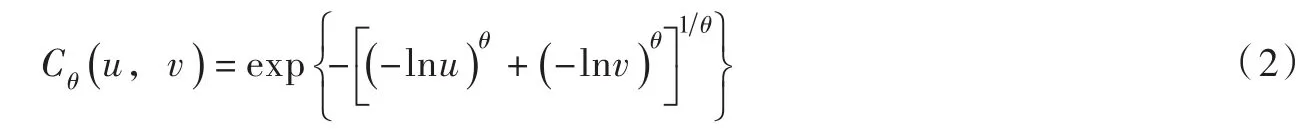
2.2 两变量洪水结构荷载重现期基本原理重现期是指给定事件连续两次发生的平均时间间隔长度。对于洪水重现期而言，通常定义为洪水危险事件发生概率的倒数[17］。就水库防洪安全而言，最重要的因素是坝前最高水位，真正的危险事件应该是坝前最高水位超过某一指定高程。因此，指定防洪标准T年一遇设计洪水的实质内涵是以此为据而规划设计出的水库工程，其防洪安全事故的风险率应恰好等于指定的设计标准（1/T）[23］。也即两变量洪水重现期可以通过坝前最高水位的单变量重现期来间接度量。采用这种方式定义的两变量洪水重现期称之为结构荷载重现期（TSL），它考虑了水文荷载（如洪峰、洪量）与水工结构的交互作用，表征的水库大坝水文失事情景更符合实际。

坝前最高水位Z与两变量水文荷载洪峰Q、洪量W的交互作用可以通过坝前最高水位函数z=g(q，w)来表征。根据坝前最高水位等值线{g(q，w)=z}定义危险区域，认为只有当洪峰、洪量组合对应的坝前最高水位值超过设定的阈值时才是危险事件。

对应的结构荷载重现期计算公式为：

2.3 基于Copula-MC法的结构荷载重现期计算步骤式（5）表明结构荷载重现期及设计值计算的关键问题是确定联合概率密度函数和坝前最高水位函数z=g(q ，w )。洪峰、洪量的边缘分布通常是非正态的且两者存在一定的相关性，另外在具有实际洪水过程线形状和复杂调洪规则的情形下积分区域边界函数通常具有非线性及分段特征，这些复杂因素都导致形如式（5）的多重积分方法在实际应用中非常困难。本文采用基于Copula函数的Monte Carlo（Copula-MC）法进行求解，具体步骤如下：

（1）根据年极值取样数据建立的洪峰洪量联合分布Cθ(u，v)，可以得到当Q为指定值q时W的条件分布，数学表达式为[20-21］：

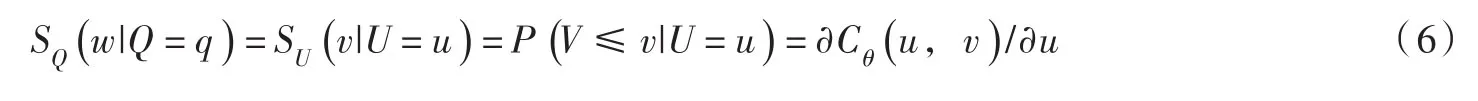
（2）产生服从[0，1］均匀分布的两个独立随机数r1和r2；

（3）令 u=r1， SU(v|U=u)=r2；

（6）选取有代表性的典型洪水过程，采用变倍比放大方法[24］获得设计洪水过程线：

式中：DFH（t）、TFH（t）分别为设计洪水过程和典型洪水过程在t时刻的流量；QD、WD分别为典型洪水的洪峰流量和洪水历时DT内的洪量；q、w表示步骤5中随机生成的洪峰、洪量。

这种方法可以保证放大后的洪峰洪量都等于指定的设计值，而且可以较好地保持典型洪水过程线的形状；

（7）将放大后的设计洪水过程线DFH（t）输入水库按调洪规则进行调洪演算，得到坝前最高水位z值；

（8）重复步骤（2）—（7）共n次，可以模拟出n个 z值，采用数学期望公式计算经验频率，获得坝前最高水位Z的概率分布曲线；

（9）对于任意给定的洪峰洪量组合（q，w），依据步骤（6）—（7）得到相应的坝前最高水位 z值，再根据坝前最高水位Z的概率分布曲线就可以查询得到对应的两变量洪水结构荷载重现期TSL；或者给定防洪标准T，令结构荷载重现期TSL等于T，根据坝前最高水位Z的概率分布曲线查询得到对应的坝前最高水位设计值ZT。

3 5种两变量洪水重现期比较及最可能联合设计值

3.1 两变量洪水重现期比较分析对目前常用的“OR”、“AND”、Kendall和生存Kendall等4种以及结构荷载（共5种）两变量洪水重现期的概念、危险区域划分依据和同一防洪标准对应的危险区域的唯一性进行总结归纳[6-9］，结果列于表1。

表1 5种两变量洪水重现期的概念、危险区域划分依据和唯一性

表2给出了5种两变量洪水重现期对应的危险事件数学描述和重现期计算公式[9，16］。其中，洪峰、洪量的单变量生存函数生存联合概率分布可以表示为：

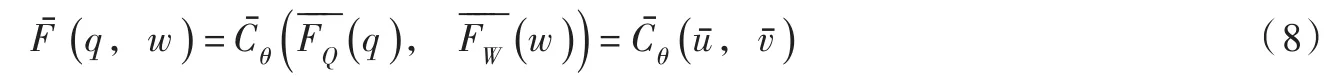
从表1和表2可以看出，“OR”和“AND”重现期均根据某一特定洪峰、洪量联合设计值定义危险区域，同一防洪标准对应的危险区域是不唯一的，大量研究表明，在安全与危险事件的判定上两者都存在着较大局限性[5-9］。与“OR”和“AND”重现期相比，Kendall、生存Kendall和结构荷载重现期的核心思想都是分别通过等值线和将多维信息组合转化为单维信息，将两变量洪水重现期表示为转化变量的单变量重现期，使得同一防洪标准对应的危险区域是唯一的，对安全事件与危险事件的判定在理论上更加协调一致。生存Kendall重现期可以解决Kendall重现期安全区域无界的问题[13］。结构荷载重现期采用坝前最高水位等值线划定危险区域，比Kendall用联合概率和生存Kendall用生存联合概率等值线更有物理基础，表征的水库大坝水文失事情景更符合实际。

3.2 最可能联合设计值当确定了两变量洪水重现期的定义方式后，一般通过假定两变量洪水重现期等于指定防洪标准T，根据一定的准则计算得到两变量洪水联合设计值。然而，对于给定的洪水两变量重现期，存在无穷多种满足设计标准的洪峰、洪量组合，它们构成了一条等值线，如何根据一定的准则科学合理地选择联合设计值成为另一个关键问题。目前洪水联合设计值选择方法主要有最可能组合法、超越概率最大组合法、条件期望组合法等，其中尤以最可能组合法得到广泛采用[6-7］。最可能联合设计值是指满足指定防洪标准T条件下，洪峰、洪量联合概率密度最大对应的联合设计值。

组合（qm，wm）即为推求的两变量洪峰、洪量最可能联合设计值。

综上，本文采用的研究方案流程如图1所示。

4 实例应用

如图2所示，隔河岩水库位于清江流域下游，坝址以上流域面积14 430 km2，具有年调节能力。该断面单峰历时一般为3～5 d，复峰可达10 d，在推求设计洪水过程线或进行水库防洪安全设计时，一般选取历时为7 d的典型洪水过程[25］。因此，本文将分析洪峰与7 d洪量的联合分布，推求洪峰与7 d洪量的两变量洪水重现期与联合设计值。隔河岩水库汛限水位为192.2 m，防洪库容5亿m3。

图1 研究方案流程

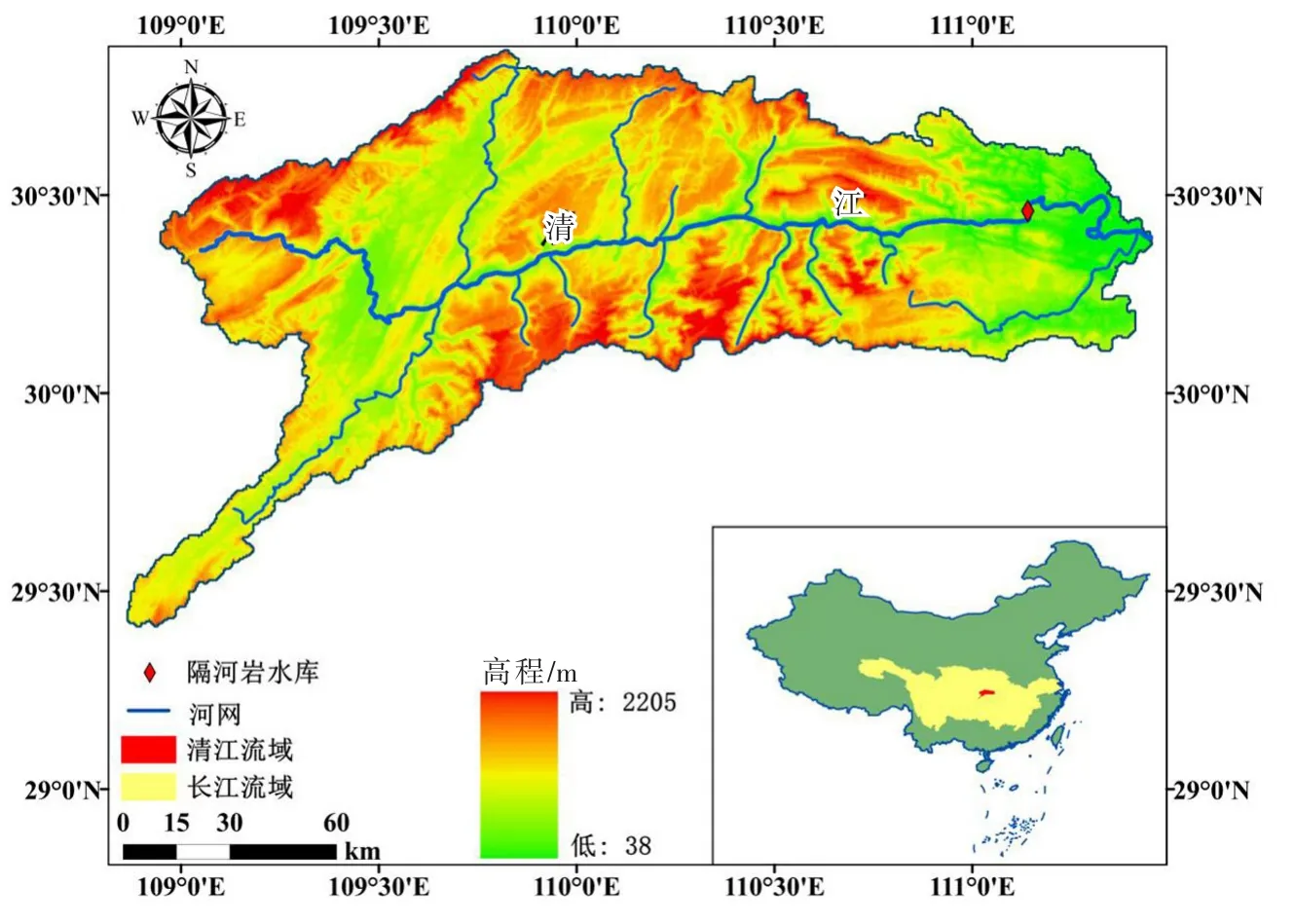
图2 清江流域隔河岩水库示意

4.1 边缘分布及联合分布的确定隔河岩水库洪峰和7 d洪量的设计参数及设计值见表3。采用Gum⁃bel-Hougaard Copula建立洪峰与7 d洪量的二维联合分布，基于1958—2010年同步资料计算得到Ken⁃dall相关系数为0.663，Copula函数的参数估计结果为θ=2.97。Cramér-von Mises检验统计量Sn=0.0232，对应的p值为0.8267大于0.05，表明建立的Gumbel-Hougaard Copula函数通过了统计检验。图3对联合观测变量的经验联合分布值与理论联合分布值进行了对比，为直观起见，按理论频率的升序排列，经验频率与理论频率值的拟合情况很好，表明所建立的联合分布是合理可行的。

表3 隔河岩水库设计洪水统计参数和设计值

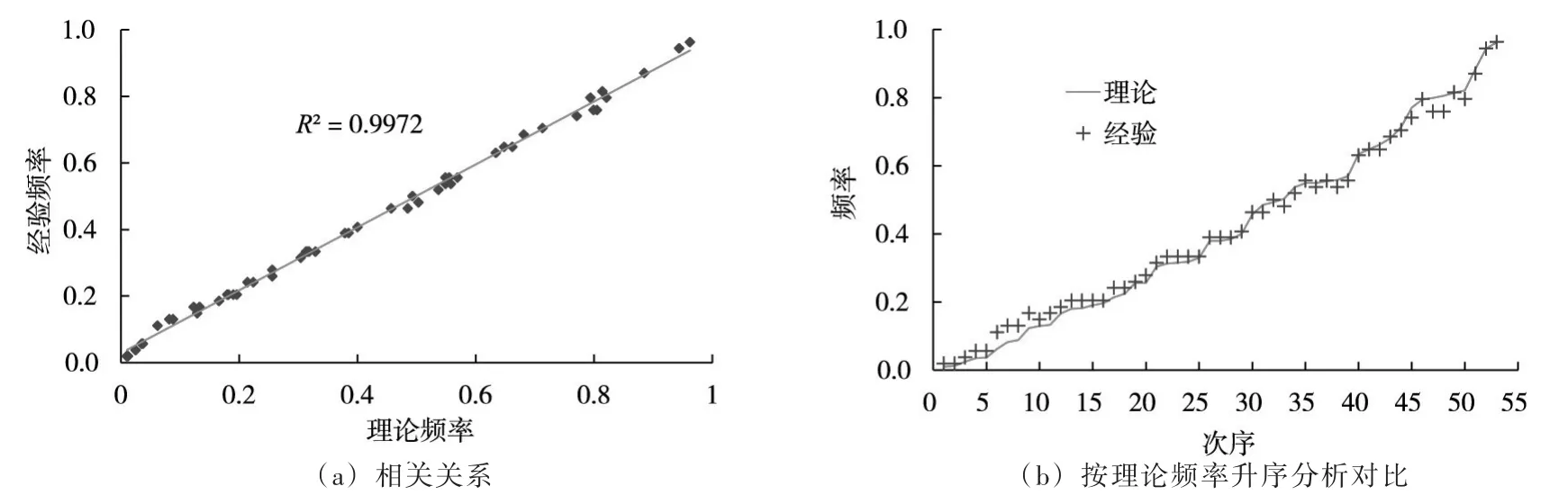
图3 联合观测值经验分布和理论分布比较

4.2 隔河岩水库坝前最高水位的概率分布按2.3节中的方法步骤，利用建立的联合分布和条件分布随机生成10万组洪峰、洪量组合，随机模拟的洪峰、洪量点据与实测值的对比见图4。由图4可以发现，Gumbel-Hougaard Copula函数能很好地捕捉洪峰、洪量的相关性结构，可以用来随机生成洪峰、洪量组合用于水库防洪安全设计。选择峰高量大、主峰靠后的1997年实测洪水为代表性典型洪水过程，放大得到10万条设计洪水过程线，并输入到隔河岩水库进行调洪演算，从汛限水位开始起调，得到10万个对应的坝前最高水位值。基于数学期望公式获得的坝前最高水位经验频率曲线（由于样本数量足够大可以近似认为是概率分布曲线），见图5。为了更好地展示结果，只给出了频率曲线的上尾部（累积概率值大于0.80，即重现期5年）。

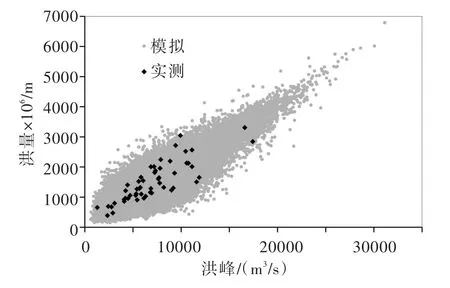
图4 随机模拟和实测洪峰、洪量点据比较

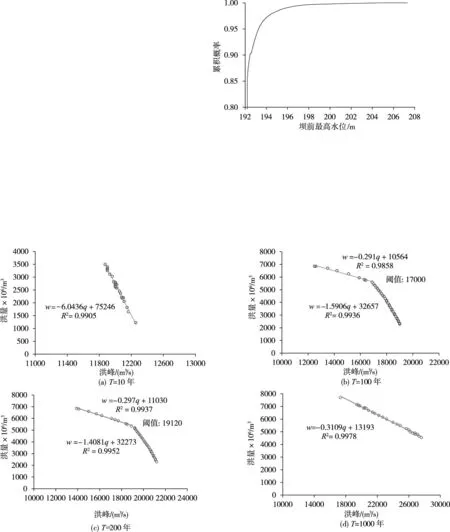
图5 坝前最高水位概率分布曲线

4.3 隔河岩水库结构荷载重现期及设计值计算本文以防洪标准T=10、100、200和1000年为例，根据图5坝前最高水位概率分布曲线就可以查询得到对应的坝前最高水位设计值ZT分别为192.45、195.86、197.19和202.88 m。为了得到满足ZT的洪峰、洪量组合，结合洪峰、洪量边缘概率分布的特点，按洪峰[10 100，27 800］m3/s以 100 m3/s等间距离散，洪量[2200，7800］×106m3以 50×106m3等间距离散，共得到20 114组洪峰、洪量组合，按1997年典型洪水过程线放大得到设计洪水过程线，输入到隔河岩水库进行调洪演算得到对应的坝前最高水位值。从坝前最高水位系列中分别统计水位192.45、195.86、197.19和202.88 m对应的洪峰、洪量组合，图6是给定坝前最高水位条件下洪量与洪峰的关系散点图。可以发现，洪量与洪峰存在显著的线性或分段线性关系，对散点进行拟合回归得到洪量与洪峰的函数关系w=h（q），具体数学表达式如图6所示。

图6清晰地揭示了水库防洪安全设计中洪水过程线洪峰、洪量存在的“异组同效”现象，即不同洪峰、洪量组合得到的坝前最高水位相同，具有等效性。回归直线的斜率值为负数表明对于给定的坝前最高水位，洪峰、洪量呈现负相关关系，洪峰越大，对应的洪量必然越小，反之亦然。如果斜率绝对值趋近于0表明调洪过程完全受洪量控制，洪峰不起作用，斜率绝对值趋近于+∞表明调洪过程完全受洪峰控制，洪量不起作用。图6中斜率绝对值均大于0小于+∞，表明调洪过程同时受洪峰洪量控制，两者都起作用。进一步分析发现，如果斜率绝对值小于1表明洪量起主要作用，洪峰起次要作用，反之大于1则表明洪峰起主要作用，洪量起次要作用。对照图6的结果，T=10年洪峰起主要作用，洪量起次要作用；T=1000年洪量起主要作用，洪峰起次要作用；而T=100年和T=200年还表现出了分段特性，随着洪峰流量的增大，由洪量起主要作用过渡到洪峰起主要作用。

结合洪量与洪峰的函数关系w=h（q），得到不同重现期结构荷载重现期的最可能联合设计值，列于表4。

图6 给定坝前最高水位条件下洪量与洪峰的关系

表4 隔河岩水库5种不同重现期洪峰、洪量联合设计值（单位：洪峰：m3/s；洪量：106m3）

4.4 洪水重现期及设计值对比研究图7给出了“OR”重现期、“AND”重现期、Kendall重现期（KEN）和生存Kendall重现期（SKEN）共4种常用的两变量重现期与结构荷载重现期（SL）洪峰洪量等值线图的对比情况，其中黑色点据为实测值。可以看出，4种重现期等值线图形状与结构荷载重现期均存在较大差异。其中，“OR”重现期等值线均位于结构荷载重现期的上方，而“AND”重现期等值线均位于结构荷载重现期的下方，表明这两种重现期都存在系统性偏差，理论上存在不足。Kendall重现期和生存Kendall重现期等值线则与结构荷载重现期存在交叉，相对“OR”和“AND”重现期更加合理。

采用3.2节中方法计算得到“OR”重现期、“AND”重现期、Kendall重现期和生存Kendall重现期的最可能联合设计值，结果列于表4中。将得到的联合设计值组合，按1997年典型洪水过程线放大得到设计洪水过程线，输入到隔河岩水库进行调洪演算得到对应的坝前最高水位值，结果见表5。根据图5坝前最高水位概率分布曲线查询得到的不同重现期坝前最高水位对应的设计标准见表6。

从表5和表6可知，由于结构荷载重现期考虑了洪峰、洪量与水库调洪规则的交互作用，其定义是基于设计洪水的实质内涵，表征的水库大坝水文失事情景符合实际，按此进行设计的水库工程正好达到指定防洪标准。与结构荷载重现期相比，“OR”重现期设计标准系统偏高，“AND”重现期系统偏低。Kendall重现期最可能联合设计值在T=10、100、200年设计标准偏低，而T=1000年偏高。生存Kendall重现期最可能联合设计值在T=10年设计标准略微偏高，T=100、200年略微偏低，而T=1000年偏高。

图7 4种常用两变量重现期与结构荷载重现期洪峰洪量等值线对比

表5 隔河岩水库5种不同重现期坝前最高水位设计值 （单位：m）

表6 隔河岩水库5种不同重现期坝前最高水位对应的设计标准 （单位：年）

5 结论

本文以超过坝前最高水位的频率来度量防洪安全设计标准，开展了具有实际洪水过程线形状和复杂调洪规则情形下的两变量洪水结构荷载重现期与最可能联合设计值计算方法研究。以隔河岩水库为例进行应用，并与常用的“OR”、“AND”、Kendall和生存Kendall两变量重现期最可能联合设计值进行比较，主要研究结论如下：（1）两变量洪水结构荷载重现期的定义考虑了洪峰、洪量与水库调洪规则的交互作用，符合设计洪水的实质内涵，能够达到指定的防洪标准。以坝前最高水位等值线定义危险区域，表征的大坝水文失事情景更符合实际，可为水库防洪安全设计提供科学依据。（2）在给定坝前最高水位条件下，隔河岩水库的洪量与洪峰存在显著的线性或分段线性关系，调洪过程同时受洪峰洪量控制，并表现出明显的“异组同效”现象，即在水库防洪安全设计中不同洪峰、洪量组合得到的坝前最高水位相同。（3）本文隔河岩水库实例中，“OR”和“AND”重现期最可能联合设计值与结构荷载重现期相比设计标准系统偏高或偏低，Kendall和生存Kendall重现期最可能联合设计值设计标准也存在不同程度地偏低或偏高的情况。

然而，本文所提方法在推求洪峰、洪量最可能联合设计值时是先确定洪峰，还是先确定洪量，顺序不同结果可能存在差异，有待进一步研究。另外，本文只选择单次典型洪水过程进行放大，所得结果具有一定的局限性，因此不同典型洪水过程对设计结果有何影响也需要进一步探讨。