四川桤木天然林和人工林的单木生长模型研究

伍小敏，徐 春，杨汉波，陈 炙，郭洪英，黄 振，王泽亮

(1.内江市东兴区农林局，四川 内江 641100；2.四川省林业科学研究院，四川 成都 610081)

树高和胸径是森林调查中最重要的两个因子，常用来计算材积、立地指数及其他与森林生长、演替、碳汇相关的重要变量[1]。相对于测量树高，胸径可以快速、方便、准确地测量[2]。生长模型一直是森林经营领域地研究热点，生长模型的种类很多，其中单木生长模型是预测林木生长，反映林分生长变化规律的基础[3]。实践中，不论是临时样地还是固定样地，树高的测定仅在一部分测定胸径的样木中进行，然后用树高-胸径关系模型来估计树高，因此构建简单而准确的树高-胸径模型是十分必要的[4]。树高曲线是指胸径(DBH)与树高(H)关系的曲线，是建立生长与收获模型的基础[5,6]。多年来，国内外学者在单木生长模型方面进行了大量的研究，取得了一系列的成果[7～10]。李海奎等[4]采用树高分级方法，建立了栎类、杉木、马尾松、杨树、落叶松和油松6个全国主要树种的树高-胸径曲线模型。童洁等[11]基于加格达奇落叶松、樟子松、红松和落叶松混合林的树高、胸径实测数据，建立了加格达奇3种森林类型树高-胸径的曲线拟合模型。代忠迪等[12]以大兴安岭3个不同生态区域的兴安落叶松实测树高-胸径数据，通过对比12个树高曲线模型，选出了适合大兴安岭不同生态区域树高曲线的预测模型。

四川桤木(AlnuscremastogyneBurk.)是四川主要的乡土树种，是营建短周期工业原料林的重要树种之一，同时也是理想的生态防护和混交造林树种。目前对四川桤木树高曲线的研究，尤其是对四川省内不同分布区树高曲线的详细研究还未见报道。本文以四川省10个地区的四川桤木天然林和人工林为研究对象，基于实测的树高-胸径数据，对9个树高曲线模型进行了拟合。基于拟合和检验统计量及模型的散点图，选出适合四川桤木树高曲线的预测模型，以期为四川桤木的树高生长预测提供科学依据。

1 材料与方法

1.1 数据来源

于2012年在四川省10个地区实测475株四川桤木的树高(H)和胸径(DBH)数据。借助围尺、测高仪测量每株林木的胸径和树高，胸径测量的精度为0.1 cm，树高测量的精度为0.1 m。将每个地区的数据随机分成80%和20%的比例分别用于建模和模型检验。本研究建模和检验数据的主要统计量见表1。

表1四川桤木树高-胸径模型建模及检验数据的统计量

Tab.1 Statistics for fitting and validation data of height-diameter models for Alnus cremastogyne

1.2 方法

1.2.1 备选模型

根据前人的研究经验和研究地区数据散点图(图1)的变化趋势，选取拟合精度较高的9个树高曲线模型(表2)。

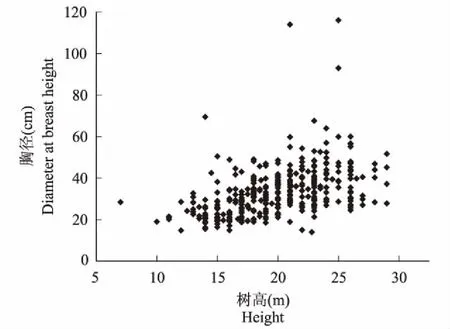
图1 四川桤木树高-胸径散点图Fig.1 Scattering plots of height-diameter for Alnus cremastogyne

表2 9种树高曲线方程

Tab.2 Nine height-diameter functions

1.2.2 模型评价和检验指标

模型评价主要采用决定系数(R2)、均方根误差(RMSE)、残差分布及参数的生物学意义等。首先利用80%的数据建模，用其余20%的数据检验；再利用独立检验样本数据，通过计算平均误差(ME)、平均绝对误差(MAE)、RMSE、相对均方根误差(ERMSE)对所建各模型进行独立性检验；最后综合考虑以上因素，选择最优树高曲线模型。

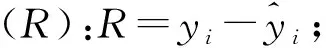
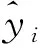
2 结果与分析

2.1 四川桤木树高曲线模型的筛选

2.2 模型检验

根据模型精度较高且误差最小的原则，本研究以模型8作为四川桤木的最优树高曲线模型。使用模型8拟合四川桤木树高时，参数a1=27.176，a2=11.856，预测值的残差分布见图2。由图2可以看出，残差无明显的异质性，表明该模型有很好的模拟效果。相关分析表明预测值与实测值具有较高的相关性， 也表明该模型具有很好的模拟效果(图3)。

表3 9种树高曲线模型拟合四川桤木树高时的误差分析

Tab.3 Error analysis of 9 height-diameter models to simulate the height ofA.cremastogyne

模型序号Models No.决定系数R2调整决定系数R2adj均方根误差(m)RMSE相对均方根误差ERMSE平均误差(m)ME平均绝对误差(m)MAE10.629 0.627 0.984 0.050 0.446 2.867 20.781 0.779 0.894 0.045 0.000 2.674 30.792 0.790 0.887 0.045 -0.003 2.651 40.767 0.765 0.903 0.045 0.010 2.709 50.791 0.789 0.888 0.045 -0.004 2.654 60.766 0.765 0.903 0.045 0.026 2.708 70.727 0.725 0.927 0.047 -0.004 2.792 80.794 0.792 0.886 0.045 0.000 2.641 90.794 0.789 0.886 0.045 0.000 2.642

图2 四川桤木最优树高曲线模型预测值的残差分布Fig 2 Residual distribution for predicted values of the optimal height-diameter model for A.cremastogyne

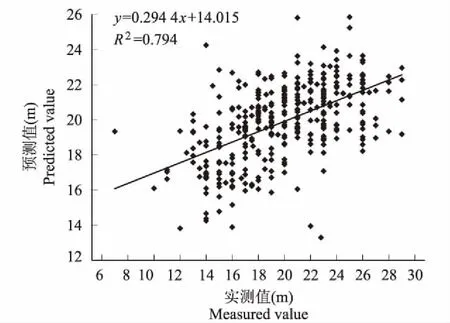
图3 四川桤木最优树高曲线实测值和预测值散点图Fig 3 Measured and predicted values of the optimal height-diameter model for A.cremastogyne

使用20%的独立验证数据对最优模型进行验证，得到模型的各误差精度指标见表4。使用独立数据验证建立的四川桤木最优树高曲线，得到的R2达0.728，RMSE为3.187，MAE为2.568，ERMSE为0.163，ME为0.125，与建模数据的分析结果基本一致。这进一步说明了本研究所建立的最优树高曲线较为合理，可以在实践中应用。

表4用独立数据验证四川桤木最优树高曲线模型的误差分析

Tab.4 Error analysis for validating optimal height-diameter model using independent data

3 结论与讨论

理论方程能在一定程度上描述生物的生长规律[3]。目前，林业工作者认为预测和实践推理是研究森林生态系统动态变化的最大挑战[24-26]。构建森林生长预估模型始终是森林工作者的首要任务[15]。本研究以四川桤木为研究对象，基于四川省10个地区四川桤木天然和人工林资源调查数据，建立了四川桤木树高曲线模型。优势木平均高则代表林分的立地状况，生长在好的立地条件下的树木，其树高也往往更高，这反映了立地条件对单个树木树高的影响[27]。虽然最优模型的自变量并未包含立地因子，但优势木平均高可以从一定程度上间接反映立地因子对树高的影响。本文所选的9个树高曲线模型中有8个模型都能较好的描述四川桤木的树高曲线(R2都达到0.72以上)。基于决定系数R2较大，均方误差(RMSE)和误差的绝对值较小的原则选择最优模型，确定模型8：H=1.3+27.176×(D/(1+D))11.856为四川桤木最优树高曲线模型。本研究建立的单木标准树高曲线模型可为四川桤木的生长预测提供依据。但是该模型目前仅限于研究地区使用，如果延伸到其他地区使用，则需要对模型进行进一步的优化、检验和验证。

马武等[2]指出竞争对蒙古栎单木生长具有一定的影响。尽管四川桤木天然林和人工林中还包含其他树种，但是由于其他树种所占的比例非常低，所以本研究并未考虑其他树种的竞争对四川桤木树高的影响。另外，本研究采用的四川桤木天然林和人工林生长观测数据具有重复性和相关性等特点，下一步可考虑采用混合效应模型法对该模型进行更新，以提高模型的估算效果。