Markov链在寿险业务利润测试模型中的应用
(五邑大学数学与计算科学学院,广东江门529020)
在寿险业务实践中,常见开发的保险产品有定期寿险、终身寿险、重大疾病保险和失能收入损失保险等.这些产品定价时均需要考虑死亡率和疾病发生率等假设.Cox和Miller、Ross分别在1965年和1995年对死亡率和疾病发生率进行研究,并最终表明这些概率随时间和年龄的变化而变化[1-2].可见被保险人基于当前状态,在下一个时间处于何种状态具有随机性,而Markov链可以很好地模拟随机特征和损失过程.文献[3]在复合生命状态模型中运用Markov链,给出了转移概率和转移强度之间的关系.张连增等[4]应用多状态的Markov链进行保费和准备金的计算.本文在上述研究基础上,应用Markov链进行保险产品开发过程的其中一项工作——利润测试.
1 预备知识
一般而言,保险公司的盈余[5]可表示为:

其中,u≥0 为保险公司的初始准备金或称前期投入,c为单位时间保费,Q (t)为累计索赔额,当U( t)<0 时,保险公司进入破产状态,将停止经营.保险公司的盈余过程与相同群体的团体保险业务的盈余过程大体相似.因此,我们在此运用保险公司的整体盈余过程作为某类团体业务的盈余过程来测试该类业务的利润等问题.在计算业务利润时,前期投入作为支付,因此保险业务的利润模型为:

在传统的利润模型中,u≥0 同样为保险公司的初始准备金或称前期投入,c通常表示为件均保费,t为保单件数,Q (t)为t件保单的总索赔额.本文采用单位时间保费和单位时间索赔额的方法,将索赔过程与不同时点对应的失能发生率、死亡率联系起来,更能符合团体寿险业务的独特之处.由于保险公司的索赔过程实际上更接近离散方式,因此本文均采用离散索赔额.对应寿险业务的索赔额Q( t)有以下表达式:

这里,q为单位时间索赔额,p(s)为保险事故发生的概率,它随时间s的变化而变化,进一步有

2 相关模型介绍
2.1 两状态Markov链团体寿险利润模型
基于生存—死亡两状态的团体寿险模型,只有生存和死亡两种状态.我们构造如下两状态Markov链:
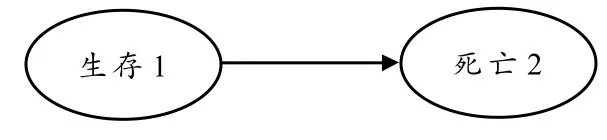
图1 两状态Markov链模型
在生存—死亡两状态的团体寿险模型中,当且仅当被保险人从生存状态(状态1)转移到死亡状态(状态2)时才进行赔付.此时概率p为:
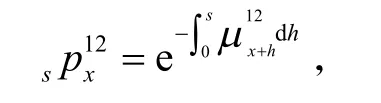

2.2 三状态Markov链团体寿险利润模型
在生存—死亡两状态团体寿险模型基础上将生存状态拆分为健康状态和失能状态的三状态团体寿险模型.被保险人从健康状态转到失能状态后可以再转回健康状态,即健康状态和失能状态是常返状态,可以无限次相互转换,一旦到达死亡状态将被吸收住.我们构造如下三状态Markov链:
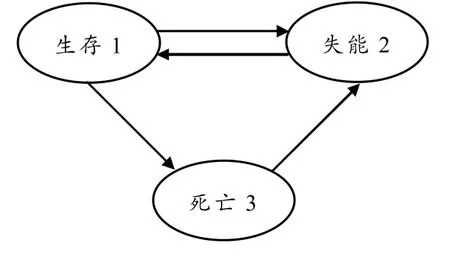
图2 三状态Markov链模型
在三状态团体寿险模型中,被保险人每次到达失能状态或者到达死亡状态时均可获得赔付.此时出险概率为x岁处于健康状态的被保险人在x+s+h岁时转移到失能状态的概率,为x岁处于健康状态的被保险人在x+s+h岁时转移到死亡状态的概率.由于此Markov链存在常返状态,转移概率需要借助Kolmogorov向前方程[6]:

通过简化计算,从健康状态转移到失能状态的转移概率为:

即状态1到状态2的转移概率等于短时间内由状态1出发最后到达状态2的概率(无论中间处于何种状态)减去转移到其他状态的概率.这里,h为步长.由于也会随着s的增加而变化,因此我们需要求出不同时间下的:

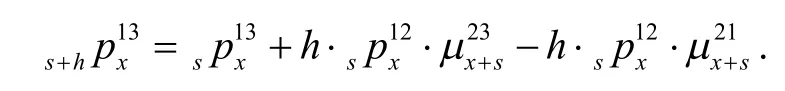
一般的,失能保额为死亡保额的一定比例,用k表示.对于任何时间t,基于三状态Markov链的团体寿险模型的利润为:
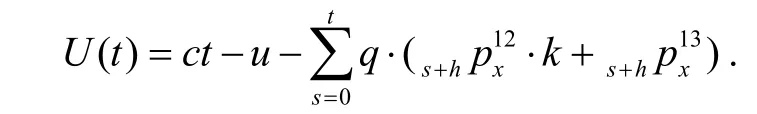
2.3 失能收入损失业务利润模型
在只承担失能收入损失责任的三状态 Markov链团体寿险模型中,当被保险人处于失能状态则连续给付保险金,一旦被保险人脱离失能状态则停止给付.与模型二不同,这里我们需要计算出团体被保险人在失能状态的持续时间.为了方便使用同一个盈余公式,我们可以转化成求被保险人在某个时间仍处于失能状态的持续概率,借助持续概率公式[3]:

同样,对任何t,失能收入损失模型的利润为:
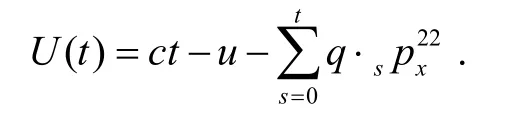
3 数值演示
下文将三状态 Markov链寿险模型应用到保险业务实践中来测算该类业务在某一时间的利润,保险公司根据此结果来做出是否扩售或者停售的决定.考虑图2所示的三状态Markov链模型,引用Dickson等[6]中的数据和如下条件:
1)从健康状态转移至失能状态的转移强度:

2)从健康状态转移至死亡状态的转移强度:

4)被保险人在其它任何状态转移到死亡状态的转移强度是一致的:.
3.1 寿险业务
假设保险公司开发一款10年期的团体寿险产品需投入50u=万元,销售时每单位时间内可收入保费200c=万元.保险期间内若被保险人死亡或失能则立即赔付.该产品可多次赔付,即当失能被保险人康复后再次失能也属于保险责任范围内.根据定价时的经验死亡率和失能发生率来确定单位时间内死亡索赔额为50q=万元,失能赔付比例定为0.1k=.该团体寿险产品的投保年龄规定为 60周岁.在该寿险产品开售第3年时,保险公司对这款产品进行利润测试来做出相应的决策.
1)首先计算出相关转移概率,采用Euler方法,令步长0.1h=,有:
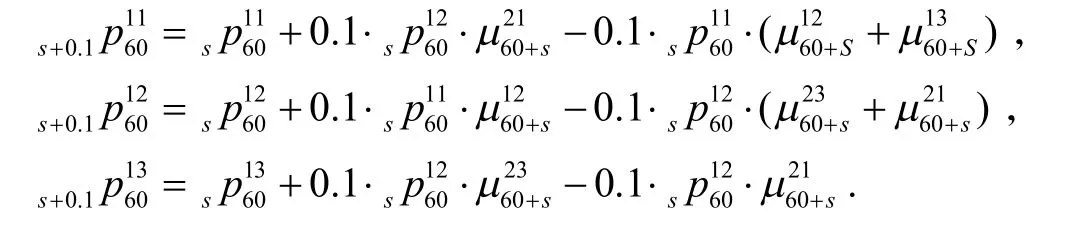
当s=0 时,,使用Matlab软件进行计算,有如下结果:

表1 相关概率结果
第3年,该寿险团体业务的利润为:

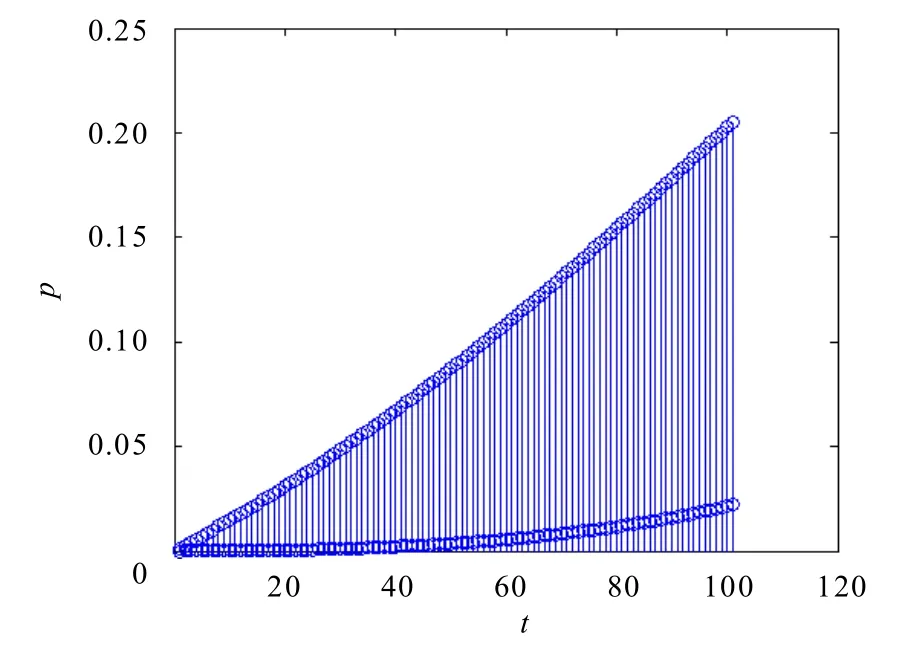
图3 失能率和死亡率趋势
把c=200,u=50,q=50,k=0.1代入,可计算得U(3)=545.885.即第3年该寿险团体业务有正的利润,保险公司可以继续加大力度销售这款产品.由于每款产品单位时间保费收入、单位时间赔付不同,具有不确定性.如果每年测试利润,会给保险公司增加工作量,我们可以通过来确保对于保险期间内任何t有利润()0U t≥.60岁健康的人在十年间的失能率和死亡率趋势如图3所示.由图3可以看出,随着时间的增加而增加,在第 10年取得,因此我们只需要计算出期满时的累计概率和.使用Matlab软件,有如下结果:

3.2 失能收入损失保险业务
假设保险公司开发的是一款失能收入损失保险,投保年龄仍然规定为60岁.被保险人处于失能状态时每年可领取保险金,为了简化,我们认为被保险人在失能状态可以连续领取保险金.该业务每单位时间内保费收入200c=万元,单位时间赔付额50q=万元.
第3年,该团体失能收入损失保险业务的利润为:

同样地,把c=200,u=50,q=50代入,使用 Matlab软件可计算得U(3)=403.9632,即第 3年,该寿险团体业务有正的利润,保险公司可以继续加大力度销售这款产品.
4 总结
本文在文献[4]的基础上,针对健康状态以及寿险业务的保障类型,运用Markov链具有的随机性特点构造成几个特定的团体寿险业务利润测试模型,包括两状态Markov链利润测试模型、三状态Markov链利润测试模型、失能收入损失业务利润模型[4].并在文章的最后对三状态Markov链利润测试模型、失能收入损失业务利润模型的实际应用进行了数值演示.并通过Matlab编程得出了与文献[6]、文献[4]结果相吻合的数值.相对于传统的利润模型,这几个 Markov链利润模型更符合寿险业务损失的不确定性特点,因此能更好地模拟团体寿险业务的索赔过程.模型的缺点在于以时间来衡量的单位时间保费、单位时间索赔额难以有效计算,需通过业务经验来判断.

