基于稳健加权总体最小二乘的点云数据圆柱面拟合
刘支亮李明峰陆建华
(1.苏州市测绘院有限责任公司,江苏 苏州215006;2.南京工业大学测绘科学与技术学院,江苏 南京211816)
0 引 言
在逆向工程、工业检测和工程测量中,圆柱面的拟合问题十分常见[1]。三维激光扫描技术突破了传统单点测量模式[2],与传统圆柱面拟合数据获取手段相比,三维激光扫描能够快速获取大量点云数据。通过圆柱面点云坐标数据的拟合处理,可得圆柱面在空间直角坐标系中的几何方程。根据圆柱面的几何关系,仅考虑观测向量的随机误差,采用最小二乘(Least Squares,LS)原理,构建经典的Gauss-Marko模型计算几何参数是最常用的拟合算法[3-5]。实际上,受仪器、扫描环境和人员等因素影响,圆柱面拟合平差模型中所有观测值都含有随机误差,即观测向量与系数矩阵均存在误差,这类模型称为EIV(Errors-In-Variables)模型[6]。总体最小二乘(Total Least Squares,TLS)法除了考虑观测值误差,还顾及系数矩阵的误差,能够得到EIV模型的最优估计[7-9]。加权总体最小二乘(Weighted TLS,WTLS)法[10]进一步考虑了观测值点位精度的差异,并根据一定准则赋予权值参与求解,从而获得更为可信的参数解。袁庆等[11]基于点位精度赋予权重,通过WTLS方法解算点云数据平面拟合参数。陈玮娴等[12]将WTLS方法应用于激光扫描球型标靶的拟合,根据点云激光回波强度特性确定先验权,提高了参数解的精度。本文根据点到圆柱面的距离与点位精度的相关性,提出顾及距离的WTLS算法,即在迭代时自适应修正观测值权,使得权值的确定更加可靠。同时,由于获取的点云数据中不可避免存在粗差点,故以3倍距离标准差为阈值,剔除粗差点,构造稳健的加权总体最小二乘(Robust Weighted TLS,RWTLS)圆柱面拟合算法,并通过实例数据验证算法的有效性。
1 圆柱面拟合数学模型
圆柱拟合参数包括大小参数和定位参数。大小参数由圆柱的半径决定,所以圆柱面的标准方程x2+y2=r2只有一个半径参数;定位参数由圆柱中轴线的位置和姿态参数两部分构成。结合圆柱的标准坐标系与测量坐标系之间的关系,圆柱面的定位参数实质上就是两个坐标系的坐标转换参数,中轴线位置参数即坐标系的平移参数,姿态参数即坐标系的旋转参数。
圆柱标准坐标系与测量坐标系之间的转换关系为:

由于标准坐标系在xoy平面内投影是一个圆,x轴与y轴方向不需要严格指定,只需两个旋转参数εX、εY就能实现姿态参数的确定,此时εZ=0,z轴指向天顶方向。另外,标准坐标系的原点可为中轴线上任意一点,即只需两个平移参数就可以确定位置,文中令。那么,原来所需求取的7个参数,实际只需要求取ΔX、ΔY、εX、εY、r共5个参数。
结合式(1),可构造目标函数为:
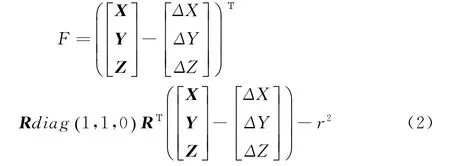
式(2)中,r为 圆 柱半 径 (r> 0),R=,且

将式(2)在近似值(ΔX0、ΔY0、(εX)0、(εY)0、r0)处以泰勒级数展开,舍去二阶及以上项,有:

则根据最小二乘原理,可列误差方程为:

式(4)中,ξ表示参数向量的改正值,ξ=,V L表示观测值误差向量,B为系数矩阵,B=,L为观测向量,

选取合适的参数初始值,求解参数向量改正值ξ,利用上次得到的参数近似值,加上本次迭代的ξ,作为新的近似值,重新计算ξ。经迭代收敛,最后得到5个参数的最佳估值,进而可得圆柱方程。
2 RWTLS算法拟合圆柱面
2.1 WTLS算法基本原理
顾及系数矩阵的随机误差,建立系数矩阵与观测向量均含有误差的EIV模型,误差方程为:

设观测值误差向量和系数矩阵误差向量服从的如下分布:

式(6)中,vec(·)表示矩阵的拉直变换,V L和vec(V B)分别为观测值和系数矩阵的误差向量,Q L、Q B为对称阵,Q L为观测值的协方差阵,且Q L,系数矩阵的协因数阵Q B可以用行矩阵和列矩阵表示:

加权总体最小二乘估计准则为:

其中,v B=vec(V B)。
2.2 权阵的定义
激光点与对象越贴近,表明测量精度越高,两者的相关性越强;反之,则说明受其他因素干扰较多,两者相关性较弱[13]。因此,可通过激光点到圆柱面的距离确定该点的权重。根据标准圆柱方程,由式(9)计算各点到圆柱面的距离。再按式(10)将距离转换成[0,1]的数值,并将其作为各点对应的权值P i。

式(9)—(10)中,D i为点到圆柱面的距离,max(D i)为点到圆柱面距离的最大值,δ为预设的一个小数值,通常取10-6,使P i不为0。那么,考虑每个点的点位精度差异,有系数矩阵B的行向量和观测向量L权阵为。假设待求圆柱面拟合参数相互独立,则系数矩阵的列向量权阵为单位阵,即P0=I5。
2.3 RWTLS求解及精度评定
利用Lagrange乘数法,可构造Lagrange目标函数为:
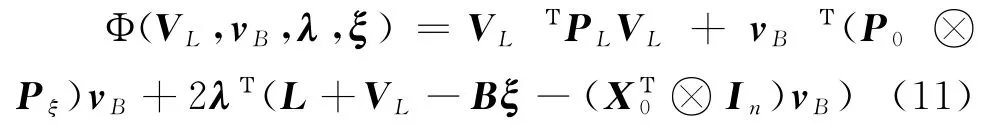
式(11)中,λ为Lagrange乘数子列向量。基于选权迭代[14]的思想,利用Schaffrin B等[10],[15]的求解算法,以3倍标准差作为阈值剔除粗差点,构造一种RWTLS算法。算法迭代计算步骤如下:
(1)由TLS解作为圆柱参数估值,计算点到圆柱面的距离,得到系数矩阵行向量和观测向量的初始权阵
(2)计算RWTLS迭代初始值:

(3)利用前一次得到的参数近似值,加上本次的ξ(i)作为新的拟合参数近似值,更新误差方程系数矩阵B和观测向量L,依据2.2节中权阵定义,更新权阵和
(4)迭代更新相关值:

(5)计算ξ(i+1):

(6)由式(15)计算点到圆柱中轴线的距离与圆柱半径的较差d i、均值和标准差:
此时,圆柱面拟合单位权中误差估值和拟合精度为:
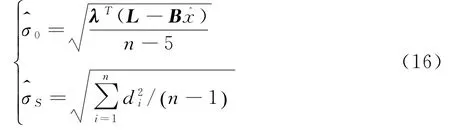
3 实例分析
利用Leica ScanStation C10三维激光扫描仪对苏州市太平天国忠王府某圆形立柱进行扫描,经配准、去噪等预处理后,得到完整的圆柱面点云。通过简化降低点云数据量,获得实验的原始点云数据(图1)。分别利用LS、TLS、WTLS、RWTLS算法对圆柱面点云数据拟合,计算圆柱面拟合精度(表1)。

图1 圆柱面点云数据分布图

表1 点云数据拟合精度结果
由表1可知,几种算法得到的最终拟合参数结果较为接近。RWTLS算法的单位权中误差明显优于LS、TLS和WLTS算法,分别相对提高了45%、45%和27%。在圆柱面拟合精度方面,RWTLS算法比WTLS、TLS和LS算法精度更高,拟合效果最好。圆柱面拟合时,迭代过程直接解算的是参数向量改正值,数值上非常小,所以TLS算法与LS算法的单位权中误差几乎一致。WTLS算法顾及距离自适应调整权阵,具备一定抗差能力,单位权中误差优于TLS算法。由于点云数据中粗差的存在,自适应权阵无法反映在计算拟合精度中,使得WTLS解算的拟合参数精度反而低于TLS算法。而RWTLS算法除了能自适应修正权值,还能探测剔除粗差,可获得更可靠的参数解,其拟合得到圆柱面的标准方程为x2+y2=0.023 313 7。
为说明本文算法的正确性,利用田晓等[5]的全站仪观测数据进行验证,得到ΔX=107.176 75 m,ΔY=225.396 40 m,εX=0°7'16.597 67″,εX=0°5'28.252 83″,r=0.124 08 m,拟合精度(即圆度的标准差[16])为0.53 mm,远优于田晓等得到的0.92 mm。结果表明,本算法是有效的,且优于传统算法。
4 结 语
(1)针对圆柱面点云数据的特点,根据圆柱面拟合的数学模型,提出了RWTLS圆柱面拟合算法,较好地顾及了不同扫描点精度的微小差异,削弱了异常值对圆柱面点云数据拟合的干扰,且可任意选取参数初始值。
(2)经过工程实例数据计算,证明了在圆柱面点云数据拟合中RWTLS算法能有效避免粗差影响,得到准确可靠的拟合参数,拟合效果优于传统算法。尽管实例的圆形柱体近似垂直于地面,但算法亦适用于大旋转角情形的柱体拟合,具有较强的工程应用价值。
(3)RWTLS解算的迭代过程较为繁琐,且收敛速度较慢,如何优化先验定权的规则提高运算效率有待进一步研究。

