“等周问题”重归高考—详解2018年高考全国I卷理科12题

广东省广州市花都区秀全中学(510800) 李桃

在周长给定并满足某些条件的所有区域中,找出面积最大的区域,这类最值问题称之为等周问题.

题目1(2006年高考全国I卷理科第11题)用长度分别为 2、3、4、5、6(单位:cm)的 5 根细木棒围成一个三角形 (允许连接,但不允许折断),能够得到的三角形的最大面积为()

分析本题中的5根细木棒“允许连接,但不允许折断”,显然,它们围成的三角形有许多.但,这里隐含着一个重要信息:这些三角形有一个共同的周长20 cm.

题目2(2013年高考全国I卷理科第12题)设△AnBnCn的三边长分别为an,bn,cn,△AnBnCn的面积为Sn,n=1,2,3,···,若b1＞c1,b1+c1=2a1,an+1=an,,则( )

A.{Sn}为递减数列

B.{Sn}为递增数列

C.{S2n−1}为递增数列,{S2n}为递减数列

D.{S2n−1}为递减数列,{S2n}为递增数列

分析因为an+1=an,所以数列{an}是常数列,即△AnBnCn的一边是固定不变的.其余两边bn+1+cn+1=,又已知b+c=2a,111可得bn+cn=2a1.那么△AnBnCn的一边是固定的,其余两边的和是定值,即△AnBnCn的周长是定值.

上述两道相隔7年的高考试题具有相同的特征:三角形的周长是定值,探究面积大小,同为“等周问题”.时隔5年,“等周问题”重归全国高考.

题目3(2018年全国I卷理科12题)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截_面面积的最大值为( )

分析根据正方体的结构特征,可将所有棱与平面α的线面角问题,转化为共顶点的三条棱的线面角问题.再根据线面角的定义,先找出一个符合题意的截面.图1中的截面B1CD1即可.将平面B1CD1平移,若向点C1方向平移,截面是三角形且面积越来越小,若向点A方向平移,截面先是六边形,当平面经过点A1时,截面是三角形A1DB,继续向点A平移,截面仍是三角形,面积相比越来越小.

弄清符合题意的截面变化趋势后,分析截面为六边形这个阶段.利用相似成比例,易知所有六边形的周长都等于△B1CD1的周长,这又是一个“等周问题”.

图1

笔者在文[1]中列出多个有助于解决中学阶段“等周问题”的等周定理的推论,其中有:

推论1在周长为定值的所有平面n边形中,以正n边形面积最大.(其中n≥3)

推论2在具有公共底边和周长的所有三角形中,等腰三角形有最大面积.

题目1的简答由推论1可知,当三角形是等边三角形时,它的面积最大.调整三角形的三边,使其尽量相等,只能是7、7、6,此时三角形面积为

题目2的简答由,可知随着n的增大,△AnBnCn逐渐趋近等腰三角形.由推论2可知,三角形面积越来越大,则{Sn}为递增数列.故选B.

题目3的简答由推论1可知,当截面是边长为的正六边形时,其面积最大为

在知道相关结论的情况下,解以上的等周问题会简洁很多.这几个结论浅显易懂,老师不妨让学生记住.此外,我们还可以关注以下结论.

推论3周长给定的正n(n≥3,n∈N)边形的面积S(n)是n的单调增函数.

推论4内接于圆的n边形面积大于其他任何有相同边(各条边的长度与排列顺序都相同)的n边形面积.(其中n≥4)

推论5在具有公共底边和周长的所有四边形中,其它三边相等时的等腰梯形面积最大.

推论6表面积一定的四面体中,正四面体体积最大.

题目4(2016届广州市普通高中毕业班综合测试(二))在△ABC中,a,b,c分别为内角A,B,C的对边,a+c=4,,则△ABC的面积的最大值为_____.

解析由化简可得2sinB=sinA+sinC,所以2b=a+c,则b=2.因为a+c=4,这是一个“等周问题”,由推论2可知,当且仅当△ABC是等腰三角形时,其面积最大,此时是边长为2的等边三角形,其面积为

图2

题目5(2015届河北石家庄模拟测试)已知平面图形ABCD为凸四边形(凸四边形即任取平面四边形一边所在的直线,其余各边均在此直线的同侧,如图2所示),且

AB=2,BC=4,CD=5,DA=3则四边形ABCD面积S的最大值为____.

解析由推论4可知,当且仅当A、B、C、D四点共圆时,其面积最大.此时A+C=π,C=π−A.由余弦定理得,在△ABD中,

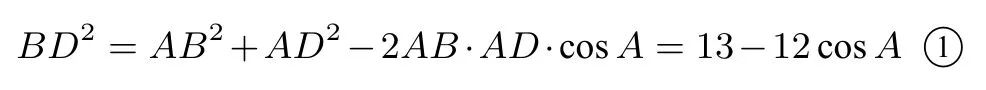
在△CBD中,

由[1]、[2]式得13−12cosA=41+40cosA,所以cosA=

以上三个高考题和两个高三模拟题考察的落脚点都是“等周问题”,这是高考命题的延续性.题目的出发点却又都不同,融合的是不同知识模块,具有一定创新性.“等周问题”一而再,再而三出现,值得广大教师和学生关注.