土钉支护边坡影响因素试验分析

李国庆，马海春，崔可锐，钱家忠

(合肥工业大学资源与环境工程学院,安徽合肥 230009)

边坡灾害是次生灾害的一种，我国的边坡灾害比较严重。2017年6月24日四川茂县特大山体滑坡造成100多人伤亡，造成巨大的人员伤害和财产损失。在边坡治理中土钉支护是常用措施之一。土钉支护是一种经济、实效、施工简单的边坡治理手段[1-2]，它充分利用土体自承力，形成自稳结构，在工程中应用较广。目前，在土钉边坡支护理论上，增量法[3-4]、能量法[5]为土钉的应用提供理论基础；在施工监测方面，国内外已开展有关边坡复合土钉的技术现场监测研究[6-10]，以及相关的模型试验研究。如莫暖娇等[11]通过设计土钉墙试验得出土钉的布置方式对土钉墙稳定性影响较大，土钉长度一致的土钉墙具有最好的稳定性。王丽萍等[12]利用铁丝模拟土钉，借助动力离心模拟试验，研究土钉加固土坡机理，验证了土钉可以提高边坡的稳定性。这些研究都分析了增添土钉可以增强边坡稳定性，但是没有分析土钉影响边坡的具体因素。本文从模型试验出发，结合工程实践经验，对土钉边坡的几个影响因素(土钉长度、土钉位置、土钉的数量及土钉倾角)进行定量分析研究，从而找出对土钉边坡支护影响较大的因素，为边坡的土钉支护工程设计与施工提供一定的参考依据。

1 试验模型及方案设计

边坡模型的框架(如图1和2)由厚6mm的钢板构成，整体尺寸底面为450mm×450mm，高500mm，斜坡长280mm，坡角 60°，通过扣具组装在一起，然后向内填土。试验用土为黄沙、黏土粉末和水，按7∶3∶3的比例混合均匀，再分层夯实预制成边坡。这种按比例制作的混合土基本符合大多数工程情况下边坡土的性质，重度为20 kN/m3，含水率为23.1%，黏聚力为15 kPa，泊松比为0.3，内摩擦角为15°。土钉模型选用直径3.5mm的铁丝[12]制成，铁丝弹性模量为210 GPa，表面未做特殊处理。

试验共设计土钉角度、位置、长度和数量4个变量。土钉角度是土钉与水平方向夹角，3种锚固角度分别为30°，50°和70°；土钉位置设为坡上、坡中、坡脚3种；土钉长度分为7和10 cm；土钉数量为5根和9根。具体试验步骤如下：①取出黏土土样，烘干击碎，将黄沙、黏土粉末和水按7∶3∶3比例混合均匀。②将调配好的试样堆填到钢模具中，用2 kg砝码进行初步压实。③在无土钉条件下对边坡进行预试验，以了解边坡发生失稳破坏时所能承受的应力范围，重新搭建边坡。④为保证边坡坡顶承受均布荷载而不是集中荷载，在坡顶位置垫一块木板，并在坡顶预置百分表，将百分表压缩至最大形变，通过加压过程中的百分表形变量表示边坡破坏的形变量，以边坡发生位移突变作为失稳判据。⑤在坡顶木板上逐级添加砝码，待百分表读数稳定后，读取边坡坡顶形变量，继续增加砝码，直至边坡失稳破坏，记录相关形变数据。⑥将沙土重新烘干，按土水比例10∶3加水搅拌均匀，重新搭建边坡，分别将土钉插入坡底、坡中和坡顶，按上述试验方法分别模拟3种情况下边坡发生失稳破坏的应力应变关系，并记录不同应力条件下边坡的形变量。⑦重复其他变量下的边坡试验。

图1 制作边坡模型Fig.1 Slopemodel

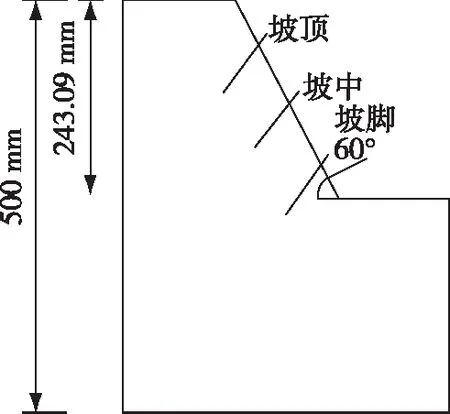
图2 边坡坡顶、坡中、坡脚土钉位置Fig.2 Soil nailing at different positions of slope

图3 无土钉时的边坡破坏Fig.3 Slope failure without soil nailing

2 试验成果分析

2.1 无土钉与加土钉边坡破坏比较分析

2.1.1无土钉边坡失稳破坏 在未施加荷载之前，以试验用土填满模具，适当平整、压实土体，确保土体形状与模具相吻合。平整土体后，在土体坡顶处放置一块轻、薄的木板(木板质量要远小于上部荷载)，随后缓慢施加荷载，直至斜坡破坏。斜坡中部偏下处出现一条明显的横向裂缝，大致呈直线状，局部略有弯曲，此直线与斜坡边界相切，呈现土体整体滑动破坏，可以发现边坡失稳破坏的滑动面处于边坡中部偏下位置(见图3)。

2.1.2有土钉边坡失稳破坏 按照同样方法制作土体边坡，放置木板，并将9根土钉以锚固角50°插入斜坡中部，土钉相距约4～5 cm，随后缓慢施加荷载，直至破坏。此过程中发现，随着荷载的增加，土钉附近土体出现细小裂缝，上部土体出现小颗粒土体滑落，甚至有部分小凹陷出现，至斜坡彻底破坏时，也未出现明显长直裂缝，土钉下部土体较上部土体破坏较少，大致呈土钉上部边坡垮塌破坏(见图4)。

图4 9根土钉位于坡中(锚固角50°)加载及破坏过程Fig.4 Loading and damaging process of slope placed with nine soil nails atmiddle of slope (anchor angle 50°)

2.2 不同土钉角度下边坡变形与荷载分析

为了分析土钉角度对边坡稳定性的影响，设计了30°,50°和70°共3种角度，研究不同角度下的变形与荷载曲线，图5为9根长土钉分别在坡顶、坡中、坡脚设计的3种角度下的变形荷载曲线。

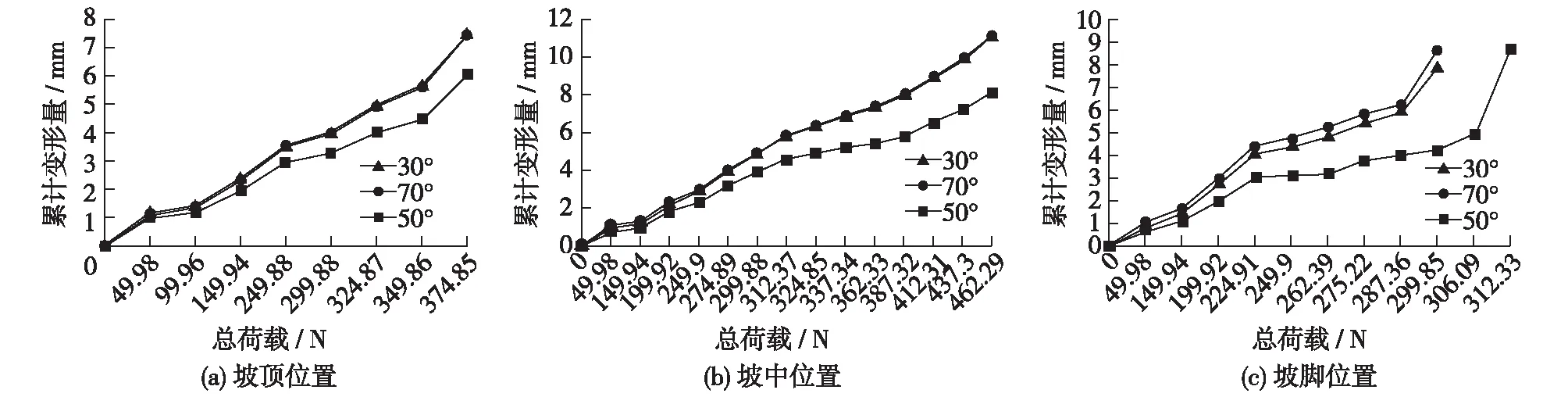
图5 9根长土钉不同设计角度下边坡沉降变形与载荷曲线Fig.5 Settlement deformation and load curves of slope under different soil nailing design angles of nine long soil nails

当土钉布置于坡顶和坡中位置时，70°土钉锚固角度支护的边坡沉降曲线和30°土钉锚固角度支护的边坡沉降曲线几乎重合，当土钉布置于坡脚位置时，土钉角度70°支护的边坡沉降曲线和土钉角度30°支护的边坡荷载变形曲线差别较小。由此可以得出：①土钉锚固角度70°支护的边坡稳定性和土钉锚固角度30°支护的边坡稳定性几乎相同；②土钉在边坡坡顶、坡中、坡脚处，土钉锚固角度50°时支护的边坡沉降都明显少于另外两种土钉角度，说明土钉锚固角度50°支护的边坡稳定性优于30°和70°时；③随着土钉倾角的增大，边坡稳定性呈先增后降的趋势，表明对锚固边坡而言存在最优锚固倾角；④50°土钉角度时边坡的滑动面靠坡后的位置较深，且滑动面较缓。30°和70°锚固角支护的边坡滑动面靠坡前的位置较浅，且滑动面较陡。

2.3 土钉位置不同边坡变形与荷载分析

对同一倾角的土钉在边坡3个位置(坡顶、坡中、坡脚)时的土坡进行变形与荷载分析，结果见图6。由图6可知：①不论土钉锚固角如何变化，当土钉位于坡中时，边坡完全破坏时累计沉降变形量最大，承受的极限荷载明显大于坡顶与坡脚位置；②边坡破坏前，土钉在坡中位置时的边坡沉降变形与坡顶及坡脚位置时沉降变形量较一致，破坏后期土钉在坡顶与坡脚位置的先达到极限荷载，土钉在坡中位置的后达到极限荷载，极限荷载为462.29 N。从无土钉边坡的分析可知，边坡失稳滑动面在边坡的中部偏下位置，所以当土钉布置于坡脚时，土钉对滑动面没有固定作用，所以效果不大。坡顶布置土钉在相同荷载下沉降量与其他模型大体相似，但中期锚固效果明显强于其他模型。这是因为土钉的抗弯作用阻碍了上部土体的下滑。而对于土钉位于坡中，滑坡体中段滑动面剪切力最大，土钉的抗弯作用发挥程度最大，最大程度限制了边坡滑移，土钉的锚固效果最好。③整体上边坡的荷载与沉降变形呈线性回归关系，30°，50°，70°时土钉在坡中位置的沉降荷载线性方程分别为：y=0.777 1x-0.775 2，y=0.552 1x-0.299 1，y=0.773 3x-0.768 6。土钉位于坡中位置时，边坡失稳破坏呈现较好的延性，破坏属于“渐进”破坏；④随着土钉在边坡施加的位置由坡顶到坡脚下移，边坡的滑动面先向坡后移动，进而又向坡外移动，然后再向坡后移动。滑动面形状由陡变缓后又变陡。

图6 土钉位置不同的边坡变形与荷载曲线Fig.6 Deformation and load curves of slope with soil nailing at different positions

2.4 土钉长度对边坡变形与载荷影响分析

由图7可知，当土钉在坡顶时，同样荷载下，短土钉边坡的变形量要稍大于长土钉下的边坡变形量，分析可见：①当土钉布置于坡顶和坡中时，相同总荷载下长土钉支护的边坡沉降量小于短土钉支护的边坡，长土钉的支护效果明显好于短土钉，此时长土钉支护的边坡有着较大的稳定性。随着土钉长度的增加，边坡稳定性有所增大。②当土钉布置于坡脚时，长土钉和短土钉支护的边坡在相同荷载下沉降量相似，说明此时边坡稳定性没有明显变化。③在土钉布置于坡顶和坡中两种情况下，长土钉在坡中时边坡减少了2.4mm的沉降量，而布置于坡顶时减少了1.1mm的沉降量。这说明长土钉布置于坡中时支护效果好于坡顶。④和短土钉边坡失稳时的破坏情况相比，长土钉支护的边坡破坏面更深，说明随着土钉长度的增加，边坡潜在滑动面逐渐往坡内移动，破坏模式由浅层滑动变为深层滑动。

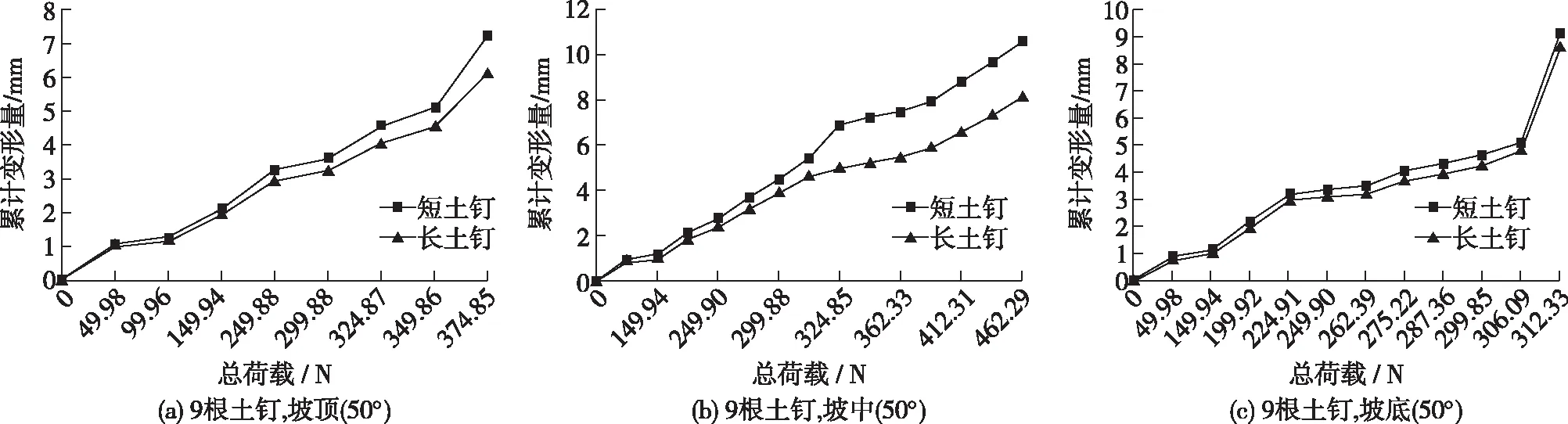
图7 使用长短土钉时边坡的沉降变形与荷载曲线Fig.7 Settlement deformation and load curves of slope with long and short soil nailing

2.5 土钉数量对边坡沉降变形与荷载影响分析

土钉数量对边坡沉降变形和荷载影响如图8所示。

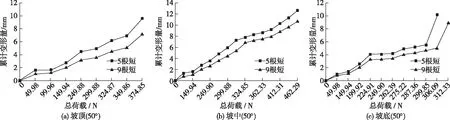
图8 土钉数量对边坡沉降变形与荷载影响曲线Fig.8 Curves of influence of soil nailing quantity on slope settlement deformation and loads

由图8可知：①当土钉在边坡位置不变时，布置9根土钉的边坡沉降量少于布置5根土钉的边坡，土钉数量多，土钉的间距变小，控制边坡沉降变形作用变强，表明土钉数量(间距)是边坡稳定性的重要影响因素。②当土钉布置于坡脚时，布置9根土钉的边坡所能承受的极限荷载稍大于布置5根土钉的边坡。对于土钉布置于坡中和坡顶的情况，土钉数量对边坡极限荷载影响不大。

3 数值模拟结果分析

采用FLAC3D软件分析试验边坡的稳定性，数值模型的尺寸与试验模型的尺寸一致，现分别计算土钉在坡顶、坡中、坡脚位置时的边坡稳定性。土钉数量为9根，土钉间距40 cm，土钉倾角为50°，计算模型见图9。

图9 不同土钉位置下的边坡数值模拟结果Fig.9 Numerical simulation results of slope under different soil nailing positions

FLAC3D数值模拟显示：土钉布置于坡顶、坡中、坡脚时，边坡安全系数分别为 0.869，1.045和1.033。土钉处于坡中位置的安全系数最大，边坡稳定性最好，与试验结果一致。

4 结 语

(1)边坡的土钉位置不同，边坡发生失稳破坏的形式不同:坡底布置土钉时，土体越过土钉顶发生失稳破坏；坡中布置土钉时，边坡极限荷载最大，对边坡的支护效果最佳，局部沿土钉顶形成一条破坏面，发生越土钉破坏；坡顶布置土钉时，土钉前土首先发生失稳破坏，在土钉前位置产生凌空面，土钉的支护效果降低。土钉布置在坡中位置，边坡沉降变形与荷载呈线性关系，边坡失稳破坏呈现较好的延性，属于“渐进”破坏，支护效果最好。数值模拟计算的边坡稳定性与试验结果一致，土钉在坡中时边坡的稳定性最高，在边坡工程中可在坡中位置重点布置土钉，坡脚和坡顶位置可以适量减少土钉数量。

(2)在土钉位置由坡顶向坡脚移动的过程中，滑动面先向坡后移动，进而又向坡外移动，然后再向坡后移动；滑动面形状由陡变缓后又变陡。

(3)当土钉数量变少，土钉间距增大时，边坡安全性明显降低，表明土钉间距对边坡稳定性有影响。在边坡施工时，减小土钉间距可增加边坡稳定性。

(4)土钉在边坡的位置不同，土钉的长短对边坡稳定性影响不同，坡顶和坡脚位置受土钉长度影响较小，但是土钉在坡中位置时，随着土钉长度在一定范围内增加，边坡稳定性呈增大趋势。随着土钉长度增加，边坡潜在滑动面逐渐往坡内移动，破坏模式由浅层滑动变为深层滑动。建议在工程实践中适量增加坡中的土钉长度。

(5)当土钉布置方式和长度不变，随着土钉倾角的增大，边坡稳定性呈先增后减的趋势。当倾角达到30°～70°时，边坡稳定性最大。当倾角超过70°后，随着倾角增加，边坡稳定性降低。试验中倾角50°时，边坡承受的极限荷载最大，边坡稳定性最好。随着倾角增大，滑动面先向边坡后沿移动，然后又朝坡前移动，滑动面先变缓后变陡。