黄姑鱼“金鳞1号”形态性状对体重的影响分析

朱 文，叶 坤，王志勇

(集美大学水产学院，农业部东海海水健康养殖重点实验室，福建 厦门 361021)

0 引言

黄姑鱼(Nibeaalbiflora)属鲈形目(Perciformes)、石首鱼科(Sciaenidea)、黄姑鱼属(Nibea)[1]，主要分布于我国沿海及西北太平洋地区。黄姑鱼是我国重要的海水经济鱼类之一，其肉质细腻，味道鲜美，受到许多消费者喜爱。但由于过量捕捞等原因，造成黄姑鱼自然资源量锐减[2]，刺激了人工养殖业的发展。目前，全国黄姑鱼养殖年产量已超过3万吨，对黄姑鱼的研究[3-7]也开展得较为广泛。对黄姑鱼的基础生物学全面深入地研究，可以为其遗传育种等研究提供必要的基础材料。

通径分析是标准化变量的多元线性回归分析方法[8]，主要用于研究多个变量之间的因果关系。Wright[9]提出应用通径分析法挖掘直接和间接效应，确定性状间作用及判断其作用大小。在育种过程中，体重作为与产量相关的有效性状之一，在不具备称量条件下，借助有限的测量条件，找到与体重显著相关的性状，即可被间接选择。目前，通径分析法已在鱼类[10-12]研究中得到广泛应用，且找到了一些与体重显著相关的形态性状，为选育工作提供了有益参考。关于黄姑鱼形态性状与体重的相关关系也有过研究报道，如刘阳阳等[13]关于6月龄雌核发育系黄姑鱼体长、体高和躯干长等8个性状的研究表明体高为影响体重的主要性状，并建立了以其研究群体为基础的回归方程；郑昇阳等[14]研究了2月龄和18月龄黄姑鱼全长、躯干长和体高等9个性状与体重的相关关系，并得出以体重为主，体高、全长或体长性状为辅选择的结论；薛宝贵等[15]对1龄黄姑鱼体长、体宽及躯干长等11个形态指标与体重进行了相关性研究，确定了体长、体高、体厚、尾柄高和眼间距为自变量，体重为因变量的最优回归方程。

本课题组从2008年起开展黄姑鱼遗传改良研究，经过连续4代选育，与未经定向选育的普通黄姑鱼群体相比，“金鳞1号”[16]具有生长快、养殖成活率较高等优点，养殖18个月平均体重和成活率可分别提高21%和25%，养殖24个月平均体重和成活率分别提高24%和30%，养殖到商品鱼规格的时间可以大大缩短，但到目前为止，对其形态学性状方面尚没有研究报道。本文对16月龄的“金鳞1号”的13种形态学性状进行相关分析、通径分析及多元线性回归分析，并通过多种显著性检验，将拟合出形态性状与体重间的最佳多元线性回归方程，旨在找出影响其体重的主要形态性状，为进一步的遗传改良提供理论指导。

1 材料与方法

1.1 实验材料

实验用鱼为本课题组2014年9月繁育的“金鳞1号”F4代，养殖于福建省宁德市霞浦县东吾洋海区。饲养管理参照常规的黄姑鱼养殖方式进行[17]。2015年12月底从网箱中随机捞取402尾16月龄黄姑鱼进行形态性状测定，其中雌鱼203尾，雄鱼199尾。

1.2 数据测定

样本的体重用电子天平测定，其他形态学指标如全长(X1)、体长(X2)、头长(X3)、吻长(X4)、眼后头长(X5)、眼径(X6)、躯干长(X7)、体高(X8)、体厚(X9)、尾柄长(X10)、尾柄高(X11)、尾长(X12)及尾鳍长(X13)等13个性状的测量方法同文献[18]，且体重精确至0.01 g，其他形态学指标精确至0.01 cm。

1.3 统计分析

测得的数据采用Microsoft Excel 2016和SPSS 22.0软件进行统计分析，利用杜家菊[19]和张琪[20]的方法，对各性状进行统计整理、相关分析、通径分析及多元线性回归分析，获得形态性状对体重的通径系数与决定系数。计算原理及方法可参照明道绪[21]的方法。计算公式为：相关系数ri=Pi+∑rijPj，直接决定系数di=Pi2，共同决定系数dij= 2rij×Pi×Pj，其中rij为性状之间的相关系数，Pi为直接通径系数，Pj为间接通径系数。

2 结果与分析

2.1 所测性状表型参数估计值

体重和各形态性状数据统计结果见表1。各性状中，雄鱼眼后头长变异系数最大(34.36%)，其次是体重(23.69%)；雌鱼尾柄高变异系数最大(23.16%)，其次是尾柄长与体重(分别为21.80%和20.39%)；雌雄变异系数最小的两个性状均为全长，分别为6.61%与6.35%。

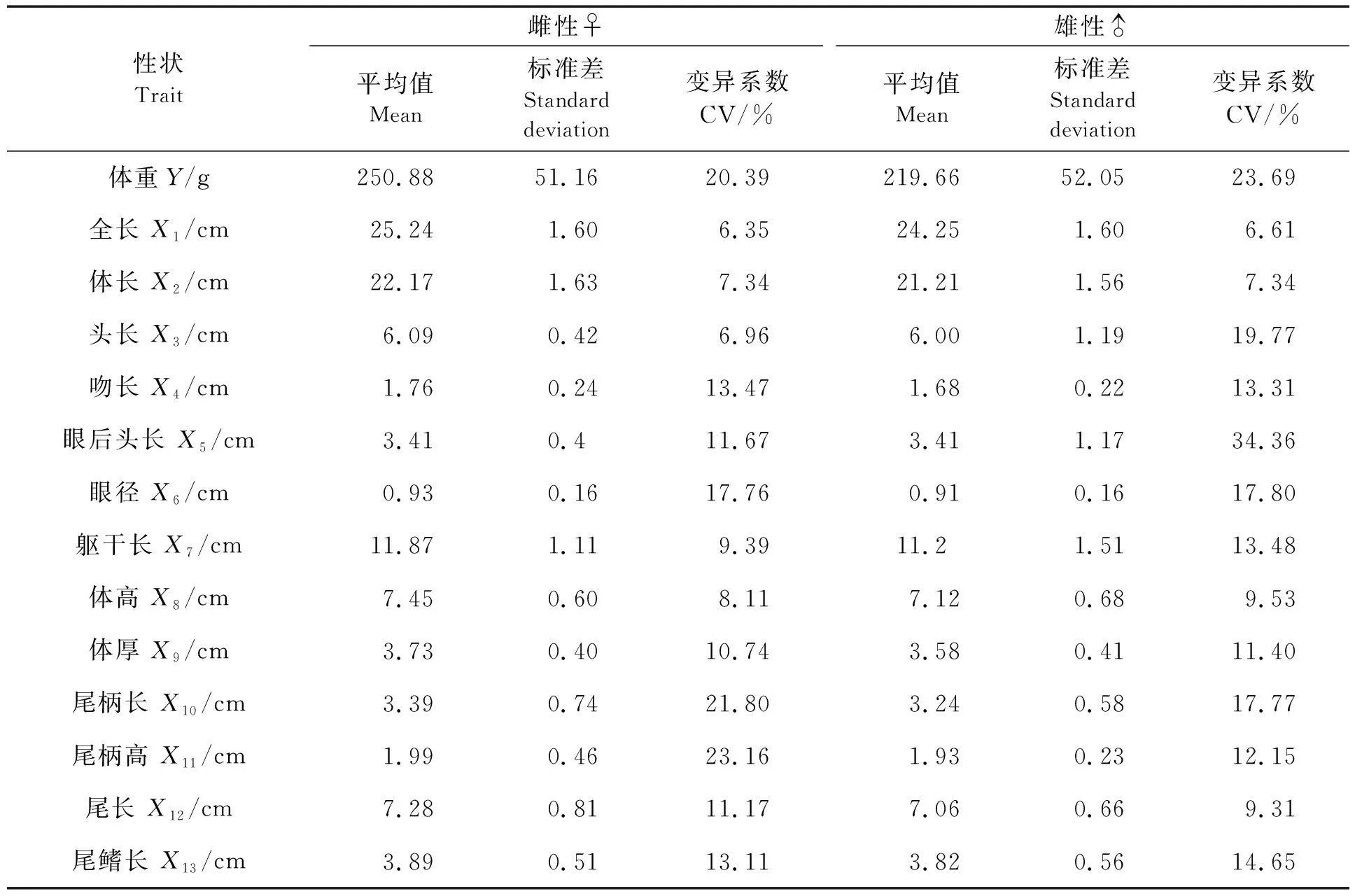
表1 黄姑鱼各形态性状的表型参数

2.2 性状间的相关分析

“金鳞1号”黄姑鱼雌性和雄性体重的频率分布直方图见图1和图2，近似服从正态分布，可以继续进行分析。两两形态性状间的相关关系如表2所示。

表2 黄姑鱼各形态性状的表型相关系数

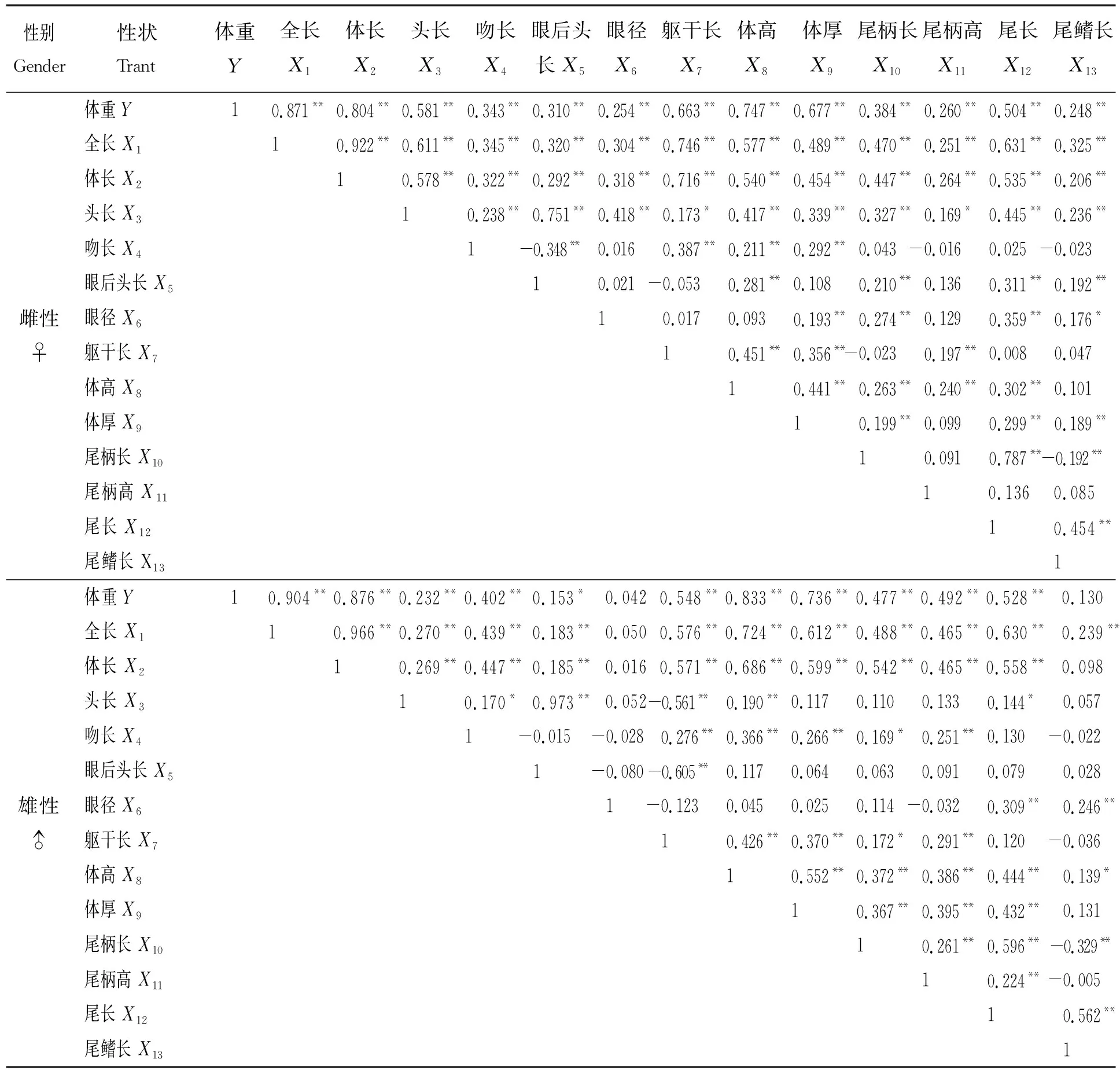
性别Gender性状Trant体重Y全长X1体长X2头长X3 吻长X4 眼后头长X5 眼径X6 躯干长X7 体高X8 体厚X9 尾柄长X10 尾柄高X11 尾长X12 尾鳍长X13 雌性♀体重 Y 10.871**0.804**0.581**0.343**0.310**0.254**0.663**0.747**0.677**0.384**0.260**0.504**0.248**全长 X1 10.922**0.611**0.345**0.320**0.304**0.746**0.577**0.489**0.470**0.251**0.631**0.325**体长 X210.578**0.322**0.292**0.318**0.716**0.540**0.454**0.447**0.264**0.535**0.206**头长 X3 10.238**0.751**0.418**0.173*0.417**0.339**0.327**0.169*0.445**0.236**吻长 X4 1-0.348**0.0160.387**0.211**0.292**0.043-0.0160.025-0.023眼后头长 X5 10.021-0.0530.281**0.1080.210**0.1360.311**0.192**眼径 X6 10.0170.0930.193**0.274**0.1290.359**0.176*躯干长 X7 10.451**0.356**-0.0230.197**0.0080.047体高 X8 10.441**0.263**0.240**0.302**0.101体厚 X9 10.199**0.0990.299**0.189**尾柄长 X10 10.0910.787**-0.192**尾柄高 X11 10.1360.085尾长 X12 10.454**尾鳍长 X13 1 雄性♂体重 Y 10.904**0.876**0.232**0.402**0.153*0.0420.548**0.833**0.736**0.477**0.492**0.528**0.130全长 X110.966**0.270**0.439**0.183**0.0500.576**0.724**0.612**0.488**0.465**0.630**0.239**体长 X2 10.269**0.447**0.185**0.0160.571**0.686**0.599**0.542**0.465**0.558**0.098头长 X310.170*0.973**0.052-0.561**0.190**0.1170.1100.1330.144*0.057吻长 X41-0.015-0.0280.276**0.366**0.266**0.169*0.251**0.130-0.022眼后头长 X51-0.080-0.605**0.1170.0640.0630.0910.0790.028眼径 X61-0.1230.0450.0250.114-0.0320.309**0.246**躯干长 X710.426**0.370**0.172*0.291**0.120-0.036体高 X810.552**0.372**0.386**0.444**0.139*体厚 X910.367**0.395**0.432**0.131尾柄长 X1010.261**0.596**-0.329**尾柄高 X1110.224**-0.005尾长 X1210.562**尾鳍长 X131

说明：**表示极显著相关(P<0.01);*表示显著相关(P<0.05)。

Notes:**means very significant correlation (P<0.01);*means significant correlation(P<0.05).

雌性和雄性各形态性状均以全长与体长的相关系数最大，分别为0.922(雌性)和0.966(雄性)。雌性各形态性状与体重的Pearson相关系数在0.248至0.871之间，均达到极显著相关(P<0.01)，相关系数从大到小依次为：全长>体长>体高>体厚>躯干长>头长>尾长>尾柄长>吻长>眼后头长>尾柄高>眼径>尾鳍长，其中以全长与体重的相关系数最大，尾鳍长与体重的相关系数最小。雄性各形态性状与体重的Pearson相关系数在0.042至0.904之间，其中除眼径和尾鳍长外，均达到极显著水平(P<0.01)，相关系数从大到小依次为：全长>体长>体高>体厚>躯干长>尾长>尾柄高>尾柄长>吻长>头长>眼后头长>尾鳍长>眼径，其中也以全长与体重的Pearson相关系数最大，而眼径最小，尾鳍长仅次于眼径，与雌鱼不尽一致。

2.3 各形态性状对体重的影响效果分析

以体重为因变量，各形态性状为自变量，利用软件SPSS 22.0，采用逐步剔除法，进行多元线性回归分析。剔除共线性严重的体长和对体重影响不显著(P>0.05)的性状，保留与体重(Y)极显著相关的性状组成最佳多元回归方程，雌性黄姑鱼的全长(X1)、体高(X8)和体厚(X9)三个性状，雄性黄姑鱼保留全长(X1)、体高(X8)、体厚(X9)和尾鳍长(X13)四个性状。对偏回归系数进行标准化，得到逐步剔除回归后与体重极显著相关的性状的通径系数，并计算相应的间接通径系数。

根据相关系数的组成效应，可将形态性状与体重的相关系数(ri)剖分成两部分：各性状的直接作用(通径系数，Pi)和两两性状间的间接作用(rijPj)，即ri=Pi+∑rijPj(见表3、表4)。表3显示，16月龄雌性黄姑鱼3种形态性状对体重的直接作用由大到小的顺序为全长>体高>体厚，而16月龄雄性黄姑鱼4种性状间接作用之和(除全长)均大于直接作用。表3、表4中VIF(variance inflation factor)值均小于10，说明本文分析结果可靠。

表3 雌性黄姑鱼各形态性状对体重的影响效果

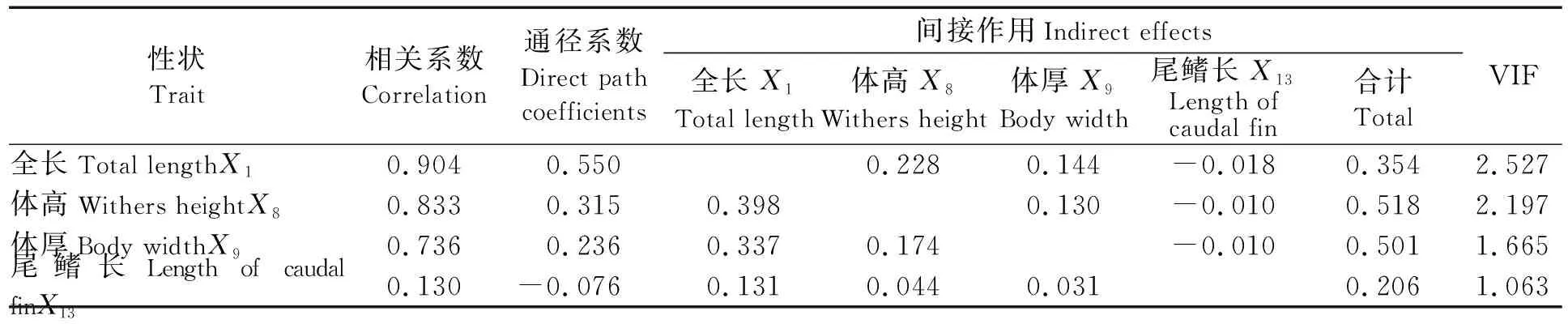
表4 雄性黄姑鱼各形态性状对体重的影响效果

2.4 各性状对体重的决定程度分析

根据各性状对体重的决定系数公式，得到单个性状及两两性状对体重的决定系数，如表5、表6所示。对角线以上的数值为两性状间对体重的共同决定系数，斜对角线上的数值为各性状单独对体重的决定系数，雌性与雄性的总决定系数分别为0.894和0.912，基本可以确定，通过逐步回归选择的性状为影响16月龄雌性黄姑鱼体重的主要性状。其中全长对体重的决定系数最大，雌性为0.318，雄性为0.303；雌性体厚和体高对体重的共同决定系数最小，为0.067；雄性各性状与尾鳍长的共同决定系数均为负值。

表5 雌性黄姑鱼形态性状对体重的决定系数

表6 雄性黄姑鱼形态性状对体重的决定系数

2.5 多元回归方程的建立

采用逐步剔除法，经显著性检验，剔除不显著的自变量，结果见表7。

表7 各形态性状对体重回归系数

以体重(Y)为因变量，雌性以全长(X1)、体高(X8)与体厚(X9)为自变量，雄性以全长(X1)、体高(X8)、体厚(X9)和尾鳍长(X13)为自变量拟合出的最佳多元线性回归方程为：

Y♀=-522.895+18.018×X1+ 25.734×X8+ 34.077×X9，

Y♂=-465.844+17.849×X1+ 24.157×X8+ 30.023×X9- 7.045×X13。

在多元回归分析中，回归平方和SSR反映了自变量共同对因变量的线性影响；残差平方和SSE体现了实验误差及不可估量因素对实验结果的影响，用F检验来分析二者之间的差别是否显著。当F值接近1，说明数据间的差异没有统计学意义；若大于1，则说明数据间有差异，且有统计学意义，自变量与因变量存在显著的线性关系[22]。表8中P<0.01，说明该样本数据间具有统计学意义，雌性全长、体高及体厚三个形态性状，雄性全长、体高、体厚和尾鳍长4个性状与体重拟合的多元线性回归方程是可靠的。

表8 多元回归方程的方差分析

说明：a—全长;b—全长，体高;c—全长，体高，体厚;d—全长，体高，体厚，尾鳍长；**表示差异极显著(P<0.01)。

Notes:a—total length;b—total length,withers height;c—total length,withers height,body width;d—total length,withers height,body width,length of caudal fin；** means very significant correlation(P<0.01).

3 讨论

本研究中测得雌性黄姑鱼“金鳞1号”16月龄个体各形态性状与体重间Pearson相关系数在0.248与0.871之间，均达到极显著相关(P<0.01)。雄鱼除眼径和尾鳍长外，其他已测性状与体重间的Pearson相关系数达到极显著，其中雌雄性黄姑鱼均为全长、体长、体高、体厚与体重的相关系数较大。雄性黄姑鱼对203尾雌鱼和199尾雄鱼测量的结果，除了眼后头长之外，其余12个性状表型测定均值都是雌鱼大于雄鱼，表明黄姑鱼雌鱼生长速度快于雄鱼，这与徐冬冬等[23]和Takita等[24]的研究结果相一致。因此，对黄姑鱼开展全雌育种研究，将具有实际应用价值。

通径分析的结果表明，16月龄雌雄性黄姑鱼“金鳞1号”的全长、体高及体厚与体重存在极显著正相关，其中全长对体重的相关系数、决定系数均最大，说明该三种形态性状即为影响体重的主要性状[25]。这与半滑舌鳎(Cynoglossussemilaevis)三种形态性状(全长、体高及体厚)对体重影响的研究结果[26]一致，但与郑昇阳[14]、薛宝贵等[15]和刘阳阳等[13]报道对黄姑鱼的同类研究结果有一定差异。郑昇阳[14]和薛宝贵等[15]报道影响2月龄黄姑鱼体重的主要性状为全长和躯干长，影响12月龄黄姑鱼体重的主要性状为体长、体高和体厚，影响18月龄黄姑鱼体重的主要性状则为体高；刘阳阳等[13]对6月龄雌核发育黄姑鱼研究的结果，影响其体重的主要性状为体长。刘贤德等[11,27]报道了影响6月龄大黄鱼(Larimichthyscrocea)体重的主要性状为头长、全长及体长，影响13月龄大黄鱼体重的主要性状则为体长与体高，影响20月龄大黄鱼体重的主要性状则为全长、体长与体高。本研究中由于体长与全长存在很强的同线性，因此在进行对体重影响的形态学性状分析时将体长剔除在外。毫无疑问，体长也是影响16月龄“金鳞1号”黄姑鱼体重的一个主要性状。这与薛宝贵等[15]对12月龄黄姑鱼及刘贤德等[11]对13月龄与20月龄大黄鱼的研究结果相一致。综合本研究以及其他研究者对黄姑鱼的研究结果，可以推测，在早期生长发育阶段(到6月龄为止)，影响黄姑鱼体重的最主要形态学性状是体长，此阶段黄姑鱼体重的增加主要依赖于体长的增长；随后，体高和体厚的增长也逐渐成为黄姑鱼体重增加的重要因素；到18月龄时，体长生长减慢，体高(以及体厚)的增长成为体重增加的最主要决定因素。这与吴常文等[3]在对东海区野生黄姑鱼年龄与生长关系的研究中发现的随着年龄增长，黄姑鱼体长生长速度不断快速下降的结果也相一致。可见，不同物种及品种在不同生长阶段影响体重的主要性状都可能存在差异。因此，有必要对不同物种及品种的经济鱼类在不同生长发育阶段开展系统的研究，以深入了解其形态学性状与体重的相关关系，从而为其遗传育种和养殖及销售管理等提供理论依据。

另一方面，本研究中标准化回归系数显著性检验结果表明，全长、体高及体厚与体重的偏回归系数均达到极显著水平(P<0.01)，所求方程成立。对回归方程进行F检验，结果表明，所拟合的多元回归方程达到极显著水平(P<0.01)，该方程有意义。因此，对于16月龄左右的黄姑鱼“金鳞1号”，可以将所选的3种形态性状作为自变量对体重进行预测和估计，其结果是可靠的。本文的结果为研究黄姑鱼形态性状的生长规律和遗传育种等提供了有用的基础材料。