地质统计学在矿床品位估算中的应用研究
邓 丹
(镇江市地质矿产研究所,江苏 镇江 212000)
地质统计学是一门以区域化变量为基础,利用变异函数研究在空间分布中具有随机性和结构性的自然现象的科学[1]。对于矿床品位估算而言,地质统计学是基于区域化变量和矿化的空间结构,借助变异函数实现品位精确估算的数学地质方法。它充分运用数理统计理论,以变异函数为核心,遵循线性估计、无偏估计和最优估计的原则,要求在估算方差极小的情况下,利用待估块段影响范围之内所有样品品位值进行加权来估计待估块段的平均品位,具有传统的品位估算方法无可比拟的优越性[2]。地质统计学分析包括区域化变量的选择、组合样统计分析、变异函数拟合、理论模型的获得和检验。
1 区域化变量
区域化变量是一种具有数值的空间位置函数,具有随机性和结构性双重性质。区域化变量应根据研究的具体任务和矿床的矿化特征来选取。根据需要,选择研究的主要成矿元素锌作为区域化变量,收集各种矿井地质勘探数据,并以此作为数据源,利用矿业软件强大的数据储存分析功能,创建矿山地质数据库。
2 样品组合分析
地质统计学遵循无偏估计的原则,即要求样本数据以固定长度加载,为此必须对样品长度不等的钻孔数据按一定的长度进行组合,其品位值以样品长度加权平均求得。组合样长度一般根据矿床类型、矿山开采的台阶(分段)高度以及品位沿钻孔方向的变异程度等因素来确定。
本研究采用进行特高品位处理后的钻孔进行组合样计算,为提高矿体内估值的准确性和实际生产需要,本文中矿体内部的样品采用2m进行组合,对于不足2m的样品,若样长大于指定长度的50%则单独作为一个信息样对待。下图为锌品位组合样的统计直方图,可以看出其基本符合正态分布。

图1 锌品位组合样统计直方图
3 变异函数模型
(1)变异函数分析
变异函数是一个距离函数,描述了不同位置变量之间的相关性。通常,随着距离h的增加,变异函数会增大,当h达到一定的值时,变异函数值会达到最大值,并且在未来保持不变[3]。变异函数可分为实验变异函数和理论变异函数。通过对地质信息的综合分析和研究,分别计算各方向的实验变异函数,拟合理论变异函数曲线。
实验变异函数是用于描述区域化变量变化规律的函数。其定义为:
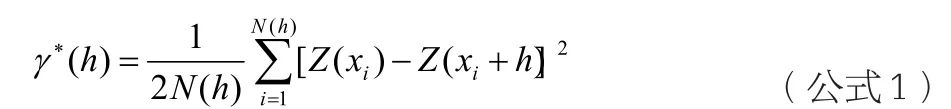
式中:h—滞后距;N(h)—滞后距为h时参加变异函数计算的样品个数;Z—区域化变量在空间点上的品位值。
如果绘制了实验变异曲线,那么实验变异曲线必须与相应的理论模型相匹配才能得到最终的结论。常用的理论模型有球状模型、高斯模型和指数模型。在本研究中,选择了应用最广泛的具有块金效应的球状模型。其一般公式为:

图2 锌品位主轴方向连续性及变异函数模型

图3 锌品位半主轴方向连续性及变异函数模型

式中:C0—块金效应; C—基台;h—滞后距;a—变程。
(2)变异函数拟合
实验变异函数是依据有限数目的地质取样数据建立的,但是通过取样只能获得由一些离散点组成的实验变异函数。因此,必须对实验变异函数进行拟合以求出球状模型相应的参数值,获得理论变异函数曲线。
为此,对锌品位做了空间72个方向上的变异函数,角度增量为5度,拟合求得球状模型相应的参数值,确定了主要方向上的理论变异函数曲线,理论变异函数曲线拟合结果见图2、图3,确定的理论模型参数见表1。

表1 锌品位变异函数拟合模型参数
(3)变异函数验证
变异函数的验证有很多方法,通常一般采用交叉验证法和离散方差验证法等。本文采用离散方差验证的方法,对得到的变异函数曲线及其理论模型参数进行可靠性检验。离散方差验证方法的原理是:利用选定的理论变异函数的参数通过克里格法估计该区域已知的样本点数据,然后将估计值与原始值进行比较,并对结果进行统计分析[4]。一般来说,离散方差验证的较好的结果是,两组数据的均值相差很小,方差近似相等,且具有良好的正相关性,从而判断理论变异函数模型参数的可靠性[5]。
换言之,验证结果应满足以下要求:区域内组合样本的实际值与克里格估计值之间的平均误差接近于0;实际数据方差与理论克里格方差的误差小于15%;两个标准差之间的误差比例大于95%。经验证,锌品位的实际值与理论估算值的均值误差为0.0129,基本趋近于0,偏差很小;实际数据方差与理论克立格方差之间的均值误差约5.75%,满足小于15%的要求;且两个标准差之间的误差比例为97.13%(大于95%),说明估算结果是无偏的,满足区域化变量的内蕴假设,可用于锌的品位估值。
4 结语
地质统计学能最大限度地利用勘探工程所提供的各种信息,提供最优、无偏的品位估算,并可给出克立格方差,该方差是度量估算精度的一个很好的尺度,是地质可靠性的一种表征,可以作为储量分级的一种依据,品位估算结果可广泛应用于矿山储量估算、采矿设计及计划编制等工作,应用前景较为广阔。

