基于定性微分博弈的网络安全威胁预警方法

黄世锐，张恒巍,2，王晋东，窦睿彧



基于定性微分博弈的网络安全威胁预警方法

黄世锐1，张恒巍1,2，王晋东1，窦睿彧1

（1.信息工程大学三院，河南 郑州 450001；2.信息保障技术重点实验室，北京 100093）

目前，基于博弈理论的网络安全研究大多采用静态博弈或多阶段动态博弈模型，不符合实际网络攻防连续对抗、实时变化的特点，为了更加贴近攻防实际进行安全威胁预警，借鉴传染病动力学模型分析安全威胁传播过程，基于定性微分博弈理论构建网络攻防博弈模型，推演安全威胁动态变化趋势。在此基础上，提出攻防定性微分博弈求解方法，构造攻防界栅以及捕获区和躲避区；引入多维欧氏距离，度量不同安全状态的威胁严重程度；进而设计预警算法，实现对网络安全威胁的动态预警，且具有更好的准确性和时效性。仿真实验结果表明，所提模型和算法有效且可行。

网络安全威胁；网络攻防；威胁预警；定性微分博弈；预警算法

1 引言

传统网络安全威胁分析方法[1-2]忽视了安全威胁的基本属性是在网络攻击和防御措施的对抗竞争中不断变化的，在准确性和可靠性上存在不足。网络安全的本质在于攻防对抗，而博弈论是研究博弈方发生直接作用时决策及其均衡问题的理论[3]，与网络攻防的基本特征高度吻合[4]。因此，采用博弈论分析推演攻防对抗行为及其相互影响，进而提出网络安全威胁预警方法，具有重要的借鉴意义和理论价值，已成为近年来的研究热点。

目前，运用博弈理论进行网络安全研究已经取得部分成果。但随着网络技术的不断发展，网络对抗过程趋于动态化、高频化、连续化，传统博弈模型[5-7]仅能分析一次攻防过程或时间间断、离散的多阶段攻防过程，已经难以满足网络安全威胁预警的时效性要求。定性微分博弈理论是在借助微分方程描述连续时间内的状态转移并分析博弈方连续决策过程的基础上，研究在攻防对抗中某一目标结局能否实现的理论工具[8]。将定性微分博弈引入安全威胁预警研究，一方面，利用微分方程分析连续时间内的网络安全威胁传播行为和安全状态迁移过程[9-10]，采用含有时间变量的连续路径表示攻防策略选取轨迹，更符合实际网络攻防行为的高频变化性和时间连续性，使威胁预警方法更具动态性和时效性；另一方面，利用该理论构造界栅面，将网络安全状态空间分为捕获区和躲避区，分别表示攻击方和防御方的优势区域，据此可以对安全威胁状态演化趋势进行动态预测与度量。但是，定性微分博弈是多维相空间中的连续变化过程[11]，网络攻防模型构建和分析难度大，据我们所知，目前尚未有公开文献对上述方法予以讨论。

本文在定性微分博弈理论的基础上，为更加准确、有效地预测网络威胁状态演化情况，将网络系统划分为不同功能的子网络，借助传染病动力学模型描述网络威胁传播过程；在此基础上，构建网络攻防定性微分博弈（NSDG, network security qualitative differential game）模型，分析攻防实时变化条件下的网络安全威胁动态变化过程；进而提出攻防定性微分博弈求解方法，构造攻防界栅划分捕获区和躲避区，并引入多维空间欧氏距离计算不同安全状态的威胁严重程度，设计安全威胁预警算法。与现有成果相比，本文方法更加符合实际情况，能够研究连续实时攻防对抗下的网络安全威胁演化趋势，并对安全威胁进行动态预警，准确性和时效性更强。

2 网络攻防定性微分博弈模型

2.1 网络安全威胁传播过程分析

由于应用场景和服务需求的不同，大型网络往往由多个业务子网构成，本文以网络功能和拓扑为边界将网络划分为多个功能子网络，利用上述网络安全威胁传播方程分析各子网络感染节点的密度状态，进而刻画整体网络中安全威胁的影响范围和严重程度，预测网络安全威胁动态变化过程并实现预警。

2.2 构造网络攻防定性微分博弈模型

基于博弈模型定义和2.1节的分析结论，考虑各子网络功能拓扑的差异性，参考文献[10]，将NSDG模型中的攻防博弈目标集边界函数定义为

3 博弈求解分析与威胁预警算法设计

3.1 网络攻防定性微分博弈求解

在网络攻防定性微分博弈模型的基础上，根据定性微分博弈理论，可将网络安全多维状态空间划分为捕获区和躲避区[8]。若当前网络安全状态位于捕获区内，则攻击方通过采取恰当的攻击策略总能使安全状态到达目标集内，实现预期目标；若位于躲避区内，则防御方采取恰当的防御措施总能抵御威胁的进一步传播，防止安全状态迁移至目标集内。因此，攻防双方都将采取最优策略进行连续对抗，避免落入对方的优势区域内，使网络安全状态在2个区域的分界面上不断迁移。而捕获区和躲避区的分界面则称为攻防定性微分博弈的攻防界栅。

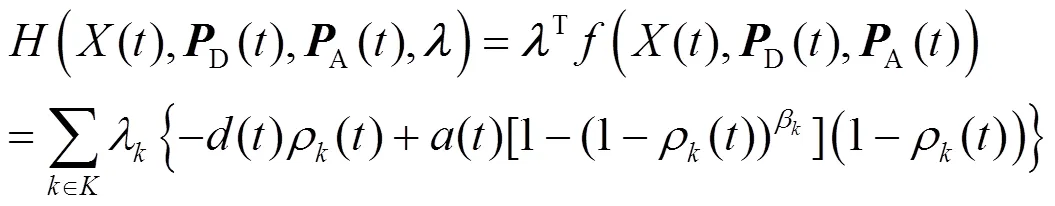
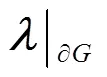
3.2 基于攻防界栅的网络安全威胁预警分析

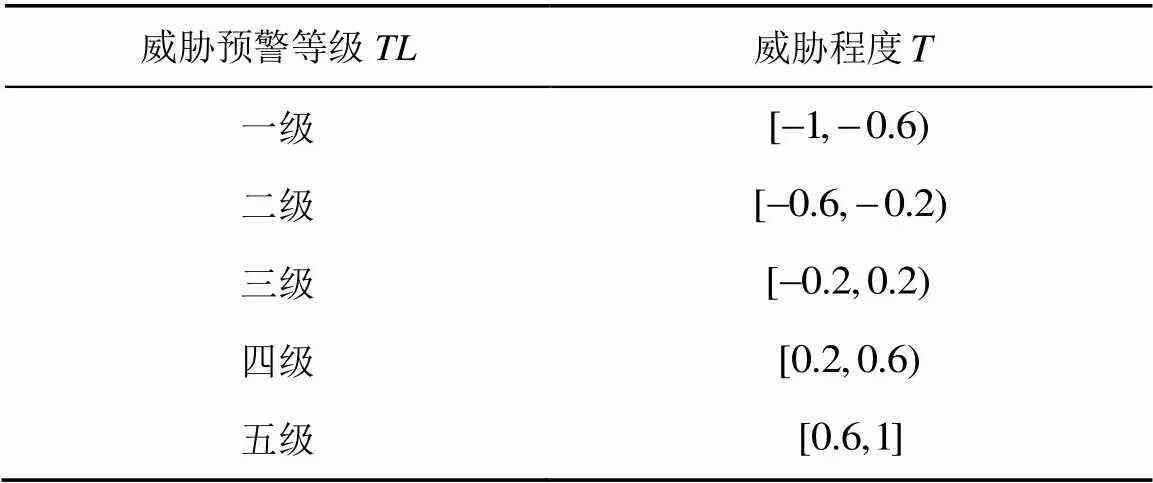
表1 威胁预警等级划分标准

3.3 网络安全威胁预警算法设计

基于定性微分博弈的网络安全威胁预警算法如算法1所示。

算法1 基于定性微分博弈的网络安全威胁预警算法

输入 网络攻防定性微分博弈模型

输出 威胁预警等级

begin

表2 本文方法和其他文献方法对比

{

14) output ()；输出网络安全预警等级

}

end

将本文方法和其他文献进行对比，结果如表2所示。模型的时效性是指攻防分析和威胁预警的有效时间。相比其他文献，本文基于定性微分博弈模型分析攻防过程预测网络安全威胁的动态变化，充分考虑了攻防双方在对抗过程中行为的动态变化性以及时间连续性，预警效果更具准确性和时效性。同时，本文模型中的博弈方类型集合和策略集合可以扩展至，具有较好的通用性，且本文给出了博弈均衡求解的详细计算过程，实用性较强。

4 仿真实验与分析

4.1 实验环境描述

通过仿真实验验证本文模型和方法的有效性。服务器使用Linux操作系统、32 GB内存、主频3.2 GHz四核CPU，并采用广泛使用的仿真工具Scalable Simulation Framework (SSFNet)，通过设定不同的网络参数模拟不同功能拓扑和规模的网络攻防场景。参考文献[16]，并结合2.1节中的网络安全攻防演化分析，从Route Views Project中得出自治系统连接数据集，用于设计实验系统的拓扑结构，采用2018年1月26日的数据（NetTF Data 20180126113000）构建网络场景，其中，综合实验平台运算能力设置网络节点总数为=1 200。为了采用三维图进行直观的演示分析，结合实验网络功能拓扑将网络划分为3个子网络，分别为数据子网、接入子网和业务子网，并设置其节点数量均为400。

结合国家信息安全漏洞库（CNNVD）数据和文献[17-18]中的漏洞信息分析方法，参照美国MIT攻防行为数据库[19]，构建网络安全攻防策略集，如表3和表4所示。

表3 攻击策略集

4.2 攻防仿真与分析

表4 防御策略集

图1 攻防界栅曲面图（为更好地展示实验结果，(a)和(b)分别为不同视角下的攻防界栅）

图2 安全状态x与攻防界栅之间多维空间距离

依据表1，网络系统当前处于安全威胁三级预警，安全状态距离攻防界栅较近，此时，网络防御方应保持高度警戒状态，开展攻击行为实时监测，并采用针对性防御策略加强安全防护程度，以防攻击方加大攻击强度造成网络安全状态进一步恶化，突破安全“红线”。

进一步根据网络安全威胁预警算法，可以确定安全状态空间内不同状态所处的安全威胁程度及对应的预警等级，并以此为依据制定不同的防御预案，提高网络系统的主动防御能力和应急处置能力。由于安全状态数量较大，本节仅展示部分威胁预警结果，如表5所示。

5 结束语

目前，基于单阶段或多阶段动态博弈模型的网络安全分析方法难以分析实时变化、连续对抗的攻防过程。本文对连续时间的网络攻防过程进行研究分析，针对威胁预警需求，提出网络攻防定性微分博弈模型，构造攻防界栅划分捕获区及躲避区，引入多维空间欧氏距离评估威胁程度；在此基础上，设计网络安全威胁预警算法，确定安全状态所处威胁预警等级并根据预警等级对网络防御提出针对性建议，仿真实验验证了所提模型和算法的有效性。研究成果为分析预测动态变化的网络安全威胁状态、实现实时安全威胁预警提供了有效的模型方法，并能够为防御方制定（选取）针对性的防御预案（策略）提供指导。

未来工作主要包括进一步研究网络功能和拓扑结构等参数对威胁动态变化的影响，提升威胁预警算法的精确性和自适应性。在结合微分博弈与多目标决策理论的基础上，研究威胁预警—防御决策一体化方法。

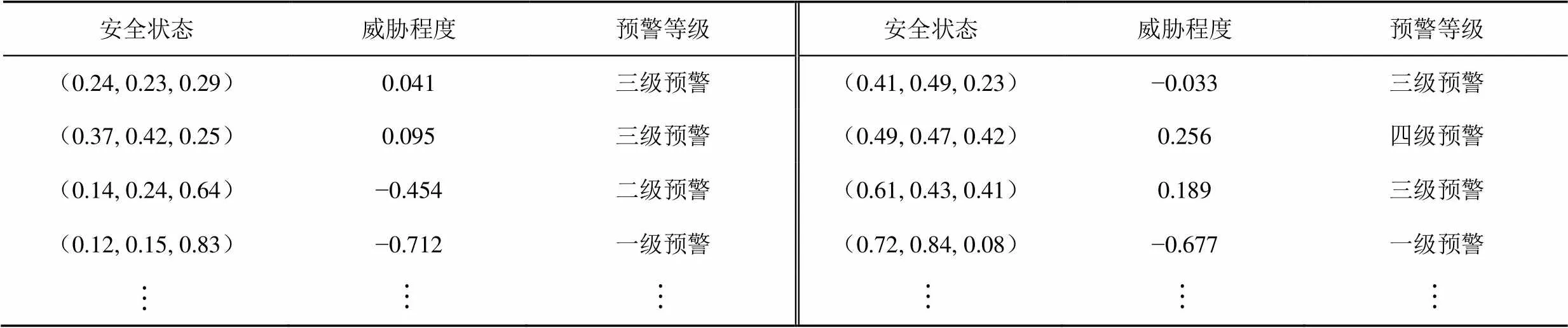
表5 部分网络安全状态所处威胁预警等级

[1] HERMANOWSKI D. Open source security information management system supporting IT security audit[C]// IEEE International Conference on Cybernetics. 2015: 336-341.

[2] KATIPALLY R, GASIOR W, CUI X, et al. Multistage attack detection system for network administrators using data mining[C]// BMJ. 2015: 1-4.

[3] FUDENBERG D, TIROLE J. Game theory[M]. Boston: Massachusettes Institute of Technology Press, 2015.

[4] 朱建明, 王秦. 基于博弈论的网络空间安全问题分析[J]. 通信学报, 2017, 32(10): 43-49. ZHU J M, WANG Q. Analysis of cyberspace security based on game theory[J]. Journal on Communications, 2017, 32(10): 43-49.

[5] WHITE J, PARK J S, KAMHOUA C A, et al. Game theoretic attack analysis in online social network (OSN) services[C]//IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining. 2013: 1012-1019.

[6] 王元卓, 林闯, 程学旗, 等. 基于随机博弈模型的网络攻防量化分析方法[J]. 计算机学报, 2015, 33(9): 1748-1764. WANG Y Z, LIN C, CHENG X Q, et al. Analysis for network attack-defense based on stochastic game model[J]. Chinese Journal of Computers, 2015, 33(9): 1748-1764.

[7] 张恒巍, 余定坤, 韩继红, 等. 基于攻防信号博弈模型的防御策略选取方法[J]. 通信学报, 2016, 37(5): 51-61. ZHANG H W, YU D K, HAN J H, et al. Defense policies selection method based on attack-defense signaling game model[J]. Journal on Communications, 2016, 37(5): 51-61.

[8] DAVID W K Y, LEON A P. Differential games theory[M]. New York: Springer Press, 2015.

[9] 张恒巍, 李涛. 基于攻防微分博弈的网络安全防御决策方法[J]. 电子学报, 2017,45(2): 431-439. ZHANG H W, LI T. Defense strategy selection method based on attack-defense differential game model[J]. Acta Electronica Sinica, 2017,45(2): 431-439.

[10] NILIM A, GHAOUI L E. Active defense strategy selection based on differential game[J]. Operations Research, 2016, 43(12): 163-169.

[11] 范红旗, 王胜, 付强. 二人微分对策问题信息模式的数学描述[J]. 电子学报, 2015, 42(2): 1355-1361. FAN H Q, WANG S, FU Q. Mathematical description for information pattern of stochastic differential games[J]. Acta Electronica Sinica, 2015, 42(2): 1355-1361.

[12] NOWAK M A. Evolutionary dynamics: exploring the equations of life[M]. Boston: Harvard University Press, 2015.

[13] ROESCH M. Snort-lightweight intrusion detection for networks[C]//The 13th System Administration Conference and Exhibition. 2015: 229-238.

[14] 余定坤, 王晋东, 张恒巍. 静态贝叶斯博弈主动防御策略选取方法[J].西安电子科技大学学报, 2016, 43(1): 163-169. YU D K, WANG J D, ZHANG H W. Active defense strategy selection based on static Bayesian game[J]. Journal of Xidian University, 2016, 43(1):163-169.

[15] 石乐义, 赵俊楠, 李芹, 等. 基于信令博弈的网络诱骗防御策略分析与仿真[J]. 系统仿真学报, 2016, 28(2):348-353. SHI L Y, ZHAO J N, LI Q, et al. Signaling game analysis and simulation on network decoy defense strategies[J]. Chinese Journal of System Simulation, 2016, 28(2): 348-353.

[16] 林闯, 王元卓, 汪洋. 基于随机博弈模型的网络安全分析与评价[M].北京: 清华大学出版社, 2014. LIN C, WANG Y Z, WANG Y. Analysis and evaluation for network security based on stochastic game model[M]. Beijing: Tsinghua University Press, 2014.

[17] LIU F M, DING Y S. Dynamics analysis of stochastic game based trust computing for networks[J]. Application Research of Computers, 2016, 33(2): 460-463.

[18] SUN W, KONG X W, HE D Q, et al. Research on attack and deference in information security based on stochastic game[J]. ACM Information security Science and technology, 2016, 27(9): 1408-1412.

[19] GORDON L, LOEB M, LUCYSHYN W, et al. 2016 CSI/FBI computer crime and security survey[C]//The 2016 Computer Security Institute. 2016: 48-66.

Network security threat warning method based on qualitative differential game

HUANG Shirui1, ZHANG Hengwei1,2, WANG Jindong1, DOU Ruiyu1

1. The Third Institute, Information Engineering University, Zhengzhou 450001, China 2. Science and Technology on Information Assurance Laboratory, Beijing 100093, China

Most current network security research based on game theory adopts the static game or multi-stage dynamic game model, which does not accord with the real-time change and continuity of the actual network attack-defense process. To make security threats warning more consistent with the attack-defense process, the threat propagation process was analyzed referring to the epidemic model. Then the network attack-defense game model was constructed based on the qualitative differential game theory, by which the evolution of the network security state could be predicted. Based on the model, the qualitative differential game solution method was designed to construct the attack-defense barrier and divide the capture area. Furthermore, the threat severity in different security states were evaluated by introducing multidimensional Euclidean distance. By designing the warning algorithm, the dynamic warning of the network security threat was realized, which had better accuracy and timeliness. Finally, simulation results verify the effectiveness of the proposed algorithm and model.

network security threat, network attack and defense, threat warning, qualitative differential game, warning algorithm

TP309

A

10.11959/j.issn.1000−436x.2018134

黄世锐（1994−），男，广东汕头人，信息工程大学工程师，主要研究方向为网络安全预警与防御决策。

张恒巍（1978−），男，河南洛阳人，博士，信息工程大学副教授，主要研究方向为网络安全与攻防对抗、信息安全风险评估。

王晋东（1966−），男，山西洪桐人，信息工程大学教授，主要研究方向为网络与信息安全、云资源管理。

窦睿彧（1981−），女，江苏江都人，信息工程大学讲师，主要研究方向为网络信息安全。

2018−03−13；

2018−07−17

张恒巍，zhw11qd@126.com

国家自然科学基金资助项目（No.61303074, No.61309013）；河南省科技攻关计划基金资助项目（No.182102210144）；信息保障技术重点实验室开放基金资助项目（No.KJ-15-110）

The National Natural Science Foundation of China (No.61303074, No.61309013), The Science and Technology Research Project of Henan Province (No.182102210144), The Opening Foundation of Sciense and Technology on Information Assurance Laboratory (No.KJ-15-110)