一种高效节能的无线传感器网络分簇路由算法

施志刚， 李桂娟， 李 亮， 张持健

(安徽师范大学 物理与电子信息学院，安徽 芜湖 241000)

0 引 言

无线传感器网络(wireless sensor networks,WSNs)在智能交通、环境监测、工业控制等领域有着相当的发展优势，但电池更换困难，因此设计一种高效节能的路由算法，最大限度地延长网络生存周期尤为重要。Heinzelman W等人[1]在2000年提出了分簇路由算法的典型代表LEACH算法。近年来,在LEACH算法基础上相继提出了多种改进方法，pLEACH算法[2]中提出将网络分区，然后在各个子区域中选出剩余能量最高的节点作为簇头；覃海生等人[3]在细胞膜优化算法的基础上通过浓度、能量和距离三因子完成对节点的分簇；罗琴等人[4]运用模糊理论计算节点担任簇头的概率来改进阈值公式；严斌亨等人[5]通过节点的剩余能量和连通度来优化簇头选举。上述算法在一定程度上降低了网络能耗，但簇头分布的随机性没有得到很好解决,且未从全局和局部两个方面来考虑簇内、簇头间的能耗问题。

本文给出了一种高效节能的WSNs分簇路由算法(efficient and energy-saving clustering routing algorithm for WSNs，ECRAW)，其特点在于：结合最优簇头数运用遗传算法(genetic algorithm,GA)和引力对簇的形成进行改进；簇头选举时考虑节点的剩余能量、节点与基站以及节点与簇中心之间的距离；引入通信代价函数建立簇头与基站的多跳通信。

1 经典LEACH算法不足

虽然相比于传统的平面路由算法,LEACH算法将网络生存周期提高了15 %[6]，但仍存在一些问题：1)簇头选举的随机性导致簇头分布不均匀；2)簇头的选举未考虑节点的剩余能量，低能量的节点担任簇头会导致簇头过早死亡，影响数据的传输，出现监测盲区现象；3)数据传输采用单跳的方式，远距离传输消耗大量的能量，不适用于大规模的无线传感网络。

2 ECRAW算法

本文从分簇方式、簇头的选举和路由方式3个方面对LEACH算法加以改进，与LEACH算法类似，每一轮也分为簇的建立和稳定传输，不同的是ECRAW算法在簇的建立阶段先进行簇的划分，再执行簇头选举。

2.1 最优簇头数

本文采用文献[7]的最优簇头数K计算方法为

(1)

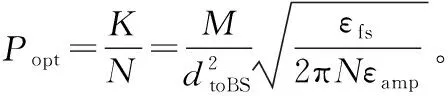
2.2 GA和引力改进簇的形成

本文采用GA优化初始聚类中心，以避免聚类效果受初始聚类中心的干扰，陷入局部最优。优化步骤如下：

1)编码方式:随机选取K个节点组成1个个体，染色体采用节点下标进行编码，即1,2,…,K；

2)初始化种群，按上述编码方式，重复H次得到种群；

3)构造适应度函数(式(2))；

4)经过选择、交叉和变异操作得到新的种群；

5)重复步骤(4)，达到最大的迭代次数，并输出种群中适应度最大的个体即优化之后的初始聚类中心。

在簇的形成过程中引入引力思想，传感节点看成是有质量无体积的质点，引力大小和簇内节点个数(质点质量)正比，与质点之间的距离成反比。由于只需比较两个引力相对大小，每次待分簇的质点在参与引力运算时，其个数一直是1，即可省略一个m，同时G可以忽略不计。为了避免簇内节点数过多，所造成引力过大带来“黑洞”问题以及簇头负载过重加快死亡现象，改进后的引力公式为

(2)

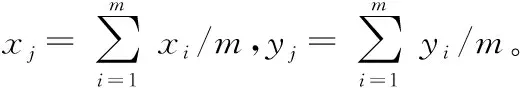
根据式(2)知，待分簇节点与簇中心的距离越小，簇内节点越多，引力就越大,该节点加入该簇的机会就越大。簇的形成过程如下：

1)设置GA运行参数，执行GA算法，适应度最大的个体即初始聚类中心；

2)基站逐一计算网络节点与K个初始聚类中心间引力大小，并加入引力较大的簇，开始成簇，并更新簇中心；

3)基站逐一计算剩余网络节点与更新后的聚类中心之间的引力大小，并更新簇中心；

4)重复步骤(3)，直到所有节点均入簇，分簇完成。

2.3 簇头选举

分簇完成之后，在簇内进行簇头的选举，结合最优簇头比例在LEACH算法基础上，考虑节点的剰余能量、节点到基站以及节点到簇中心的距离，得到新的阈值为

(3)

(4)

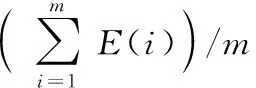
每轮中节点通过rand(1,1)随机产生1个数，若小于式(3)，节点当选为该簇的簇头，重复上述过程，在每个簇中选出簇头。改进后的阈值计算公式使剩余能量较多、距离基站和距离簇中心较近的节点有更多的机会当选为簇头，在一定程度上使簇头分布均匀，均衡网络能耗。

2.4 稳定传输

ECRAW算法整体流程如图1。

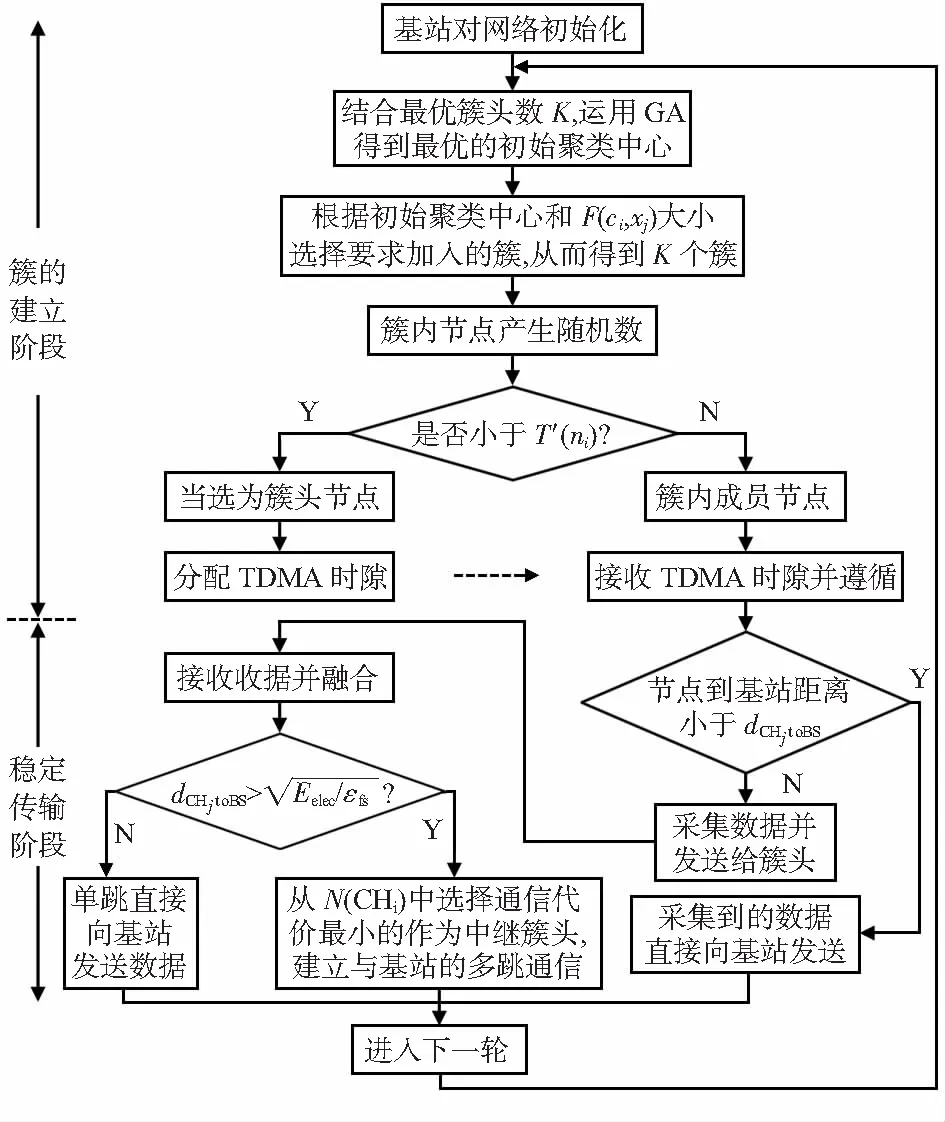
图1 ECRAW算法工作流程

3 算法仿真及对比分析

3.1 实验网络参数

为了验证ECRAW算法的性能，采用一阶无线通信能耗模型[8]，本文通过MATLAB 2014a平台将其与LEACH,LEACH-EC算法[5]在死亡节点数、剩余能量和消耗能量3个方面进行了仿真比较。设有100个初始能量为1J的节点随机部署在100 m×100 m的区域中，基站位于(50 m,50 m)处，实验的相关网络参数如下：数据包长度4 000 bits，εfs为10 pJ/bit/m2，εamp为0.001 3 pJ/bit/m4，数据融合能耗EDA为5 nJ/bit，收发电路能耗Eelec为50 nJ/bit。

3.2 仿真结果

评价网络的生存周期通常看第1个节点死亡时间(first node dead-time,FND)和1/2节点死亡时间(half node dead-time,HND)。图2中相比于LEACH和LEACH-EC算法本文算法从FND到最后一个节点死亡时间均滞后，延长了网络的生存周期。本文算法FND出现在第2 375轮，较LEACH提高了1.64倍，较LEACH-EC延长了58.4 %；HND出现在2 521轮，较LEACH提高1.09倍，较LEACH-EC延长23.3 %；另外图中本文算法的曲线陡峭，说明节点能量消耗均衡性较好，可见，本文算法具有明显的优势，主要原因是改进了簇的形成和簇头的选举，使簇头分布更均匀，簇头与基站通信的机制的改进降低了网络能耗。

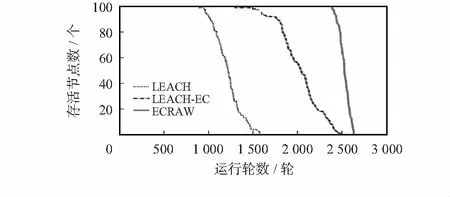
图2 网络生存周期对比

随着网络的运行，图3说明了网络能量在不断消耗，相比之下，在相同的时间内，运用本文算法消耗的总能量少于其他2种算法；相同的初始能量下，总能量耗尽较晚。图4中本文算法的剩余能量高于其他2种算法，表明了在相同的初始能量下，改进后的算法较LEACH 和 LEACH-EC 能耗较小，有效地节约能量，另外，ECRAW算法倾斜度较为平缓，说明网络性能较为稳定。

图3 消耗总能量对比

图4 剩余总能量对比

4 结束语

本文在LEACH算法的基础上提出了一种ECRAW算法，仿真结果表明，该算法在存活节点个数、消耗总能量和剩余总能量方面均优于 LEACH 和LEACH-EC算法，有效降低网络能耗，均衡了节点能量消耗，延长了网络生存周期。