编码精度自调节的心电压缩ASIC

徐焕章， 罗嘉蕙， 陈志坚

(浙江大学 电气工程学院，浙江 杭州 310027)

0 引 言

心电(electrocardio,ECG)压缩技术可以降低ECG信号传输的功耗[1]。具有时频局部化和多分辨率特性的小波变换法[2]可获得较高的压缩率，广泛应用于ECG压缩领域。但由于小波变换是基于傅里叶变换的卷积运算[3]，计算复杂度高，对存储空间的要求也很高，硬件实现成本与功耗均较大。

鉴于此，Daubechies和Sweldens提出了提升格式小波变换[4]，摆脱了基于傅里叶变换的卷积运算，简单快捷。在量化编码上，Shapiro提出了嵌入式零树小波(embedded zerotree wavelet，EZW)编码。该编码方式利用小波变换各级系数具有方向性的特点进行渐进式编码[5]，相对于其他编码方式，计算相对简单且压缩能力强，目前主要用于二维图像[6]压缩领域。

针对现有ECG压缩专用集成电路(application specific IC,ASIC)实现成本较大且压缩率不稳定的问题，本文提出了基于提升小波的编码精度自调节的ECG压缩ASIC，利用小波变换得到各级高频系数和以初始编码阈值为依据动态调节电路的编码精度；在硬件编码中，将传统的自顶向下扫描方式改进为自底向上，摆脱了EZW编码中大量出现的递归运算[7,8]，大幅减少扫描次数，并降低硬件运算复杂度和动态功耗。

1 自调节算法原理

本文在算法上，主要对EZW编码进行了改进，并在压缩过程增加了动态调节编码精度的部分。

1.1 5/3提升小波变换

“5”和“3”代表该小波变换的高通和低通分解滤波器的长度。分解过程分为分裂、预测和更新，如图1所示。

5/3提升小波变换的算法公式为

(1)

式中x(n)为原始信号，d(n)，c(n)分别为高、低频系数。

图1 提升小波变换

1.2 逆向扫描的EZW编码

1.2.1 传统编码方法

传统EZW编码算法如下：经过n级小波变换后，高频系数被分解为n层的二叉树结构，称为零树。每个粗尺度(第i级)系数对应2个较细尺度(第i-1级)系数，对应关系可用父节点和子节点的关系描述，如图2所示。EZW算法中，对于一个零树，扫描顺序按照编号顺序进行扫描编码。

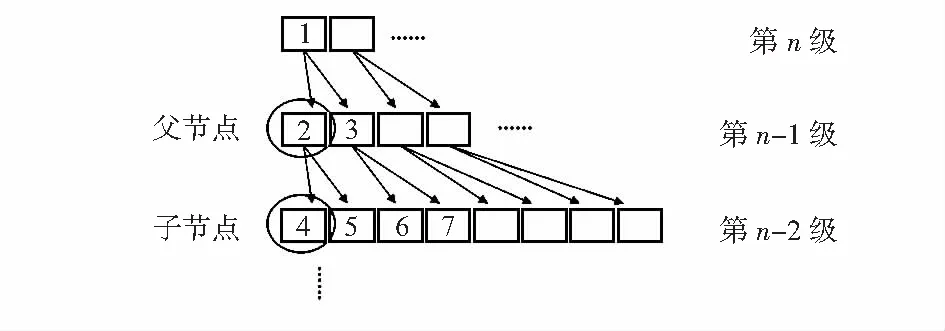
图2 零树的构成

1.2.2 逆向扫描编码

本文设计的算法对传统编码进行改进，将每个节点的遍历次数由多次变为仅需要1次，使得运算复杂度成倍减少。先确定子节点的编码，再确定父节点的编码，因此在判断子节点均编码T(零树根)过程中只需遍历其2个子节点即可。当得到零树根时，将其子节点的编码删除，从而实现零树根的子孙不编码。

通过对比可以看出：当零树深度为N时，传统编码方法的运算复杂度为O(2N×N)；采用逆向扫描的方式后，运算复杂度降低为O(2N)，例如采用5级小波变换时，零树深度为5，则运算次数由160(32×5)次减少为32次。

1.3 编码精度自调节

自调节的依据在于，压缩率和重要系数的分布有关，而重要系数的分布又反映了信号的抖动程度。当一个信号的抖动幅度越大，在同样编码精度下，其压缩率就会越低。为了保持较为稳定的压缩率，需要针对不同信号使用不同的编码精度。考虑到硬件实现开销，提出了一种低复杂度的编码精度自适应调节算法：1)对于5级小波变换，选取了第4级和第5级的误差序列均值作为参考用于预测此时信号的抖动误差因子G0。2)考虑到初始阈值T0，引入相对误差因子g0=G0/T0，g0的值很大程度上体现了初始阈值T0确定的情况下，重要系数的占比和EZW的编码效率。设S0为精度参数，表示精度增加的比特数，即编码总轮数。当g0处于不同范围时，S0的取值为

(2)

通过简单的线性运算和比较，实现了样本编码精度的自调节。提高了低压缩率样本的压缩率，从而提高了整体压缩率。

2 硬件结构设计

本文处理的数据为以128个点为1帧的数字心电信号，输出这一帧数据的编码。整体结构框架如图3所示。

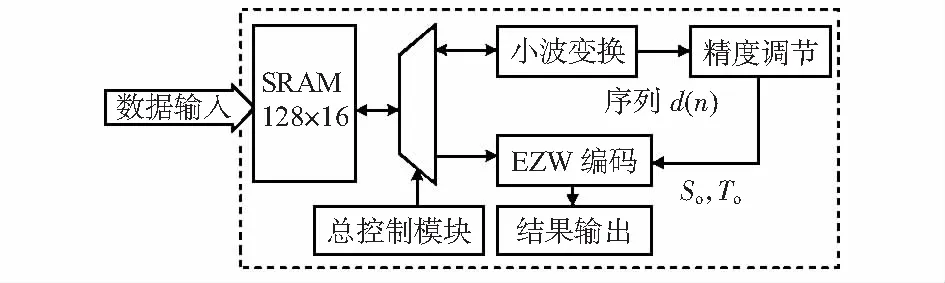
图3 整体硬件结构

由图3可知，硬件主要由小波变换模块、精度调节模块和EZW编码模块构成。除此之外，由块深度为128 bit，宽度为16 bit的静态随机存储器(static random access memory,SRAM)用于存储原始数据，以及小波变换后的高频、低频系数；总控制模块用于控制不同阶段下各个模块对SRAM的访问，同时也控制各个阶段之间的切换并广播给各个模块。

2.1 小波变换模块

小波变换模块可以实现同址运算， SRAM中的奇序列和偶序列被高频和低频系数取代，这样的同址运算所消耗的运算资源以及额外的存储资源最优。由式(1)可以看出，每得到3个原始信号点x(2n),x(2n+1)和x(2n+2)，就可以计算出d(n)，进而通过d(n)和d(n+1)计算出r(n)。据此，需要一个深度为3的先入先出(first in,first out,FIFO)存储原始信号，且需要2个寄存器D和R分别存储d(n)和r(n)的值。才能保证d(n)和d(n-1)能够同时存在，在每次计算r(n)时，d(n)的值通过组合逻辑得到，d(n-1)的值从寄存器D中获得，最终将d(n)更新到寄存器D中，如图4所示。

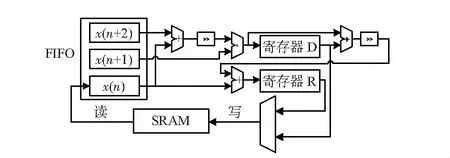
图4 小波变换模块电路

每次得到d(n)和r(n)会写入SRAM中x(2n)和x(2n+1)原本所在的位置。然后将x(2n+3),x(2n+4)读入FIFO中，进行下一组系数运算，直到一级小波变换完成，再将r(n)作为新一级变换原信号序列。

2.2 精度调节模块

该模块的主要功能是计算初始阈值，进一步计算精度参数。求阈值时，首先暂存绝对值最大的高频系数，当出现高频系数d(n)比当前最大值大时，将最大值更新为新的高频系数d(n)。根据式(2)求解精度参数。

2.3 EZW编码模块

编码模块由两个状态机进行维护，主状态机为有限状态机(finite state machine,FSM1)主要根据精度参数来控制多轮的编码。副状态机FSM2负责每一轮编码时对零树进行主扫描和辅扫描。编码模块的两个状态机的协同工作状态如图5所示。

图5 编码模块状态

1)在FSM1中，开始编码之后，各状态如下所述：

a.扫描(SCAN)：开始编码，激活FSM2，监测到一轮编码结束之后进入重复(REPEAT)状态。

b.REPEAT：检查是否编码精度已经达到由精度调节模块设定的精度参数：若是,进入输出(OUTPUT)状态;否则,将阈值减半，回到SCAN状态编码。

c.OUTPUT：将一棵零树的编码逐点输出。

d.重新载入(RELOAD)：将阈值重置为初始阈值，检查是否已经完成了一帧的扫描。

2)在FSM2中，接收来自FSM1的激活信号之后，开始扫描，各个状态如下所述:

a.读取(READ)：从SRAM中读取系数，读取顺序自底向上。

b.编码(CODE)：根据改进后的方法进行编码。

c.CNT：确定正在扫描哪一级的系数，从而确定读取和编码时的索引，如果最顶级已经扫描完成，则发送完成信号给FSM1，使其从SCAN状态进入REPEAT状态。

3 实验与结果分析

3.1 压缩性能实验

压缩率是ECG压缩ASIC的关键指标之一，本文以MIT-BIH数据库的心电信号为测试样本，采用压缩率(compression ratio，CR)和失真度计算方法是百分比均方根误差(percent root mean square difference,PRD)来衡量该算法的压缩性能。本文添加了编码精度自调节功能，表1为编码精度固定为4时的压缩率和编码精度自调节后的压缩率对比。

表1 编码精度固定和自调节的压缩率对比

可以看出：选取的几个样本，在固定的编码精度下，CR波动较大，其中样本102，104，109，203的CR较低,经过编码精度自调节之后，各样本的CR都保持在高水平。

压缩性能如表2所示，从表中可以看出，相对于其他算法，本文算法在失真度低的情况下，压缩率高，有利于减少传输功耗和存储资源。

表2 测试样本的压缩性能

3.2 电路实验数据

采用SMIC 40 nm工艺，电路面积仅有7 387 μm，折合成9 885个等效门。选取1 MHz作为系统频率，在1.1 V供电电压下，电路总功耗为7.11 μW，其中,4.97 μW为静态功耗，主要来自SRAM的漏电功耗。本文设计的ASIC和文献[11]的电路参数对比，在2种设计都采用EZW编码进行压缩的情况下，本文通过降低电路的复杂度极大地减少资源，等效门数减少了3倍，又通过工艺尺寸的减小，使得整体电路面积缩小了32.3倍。虽然本文设计频率略低于文献[11](250 MHz)，但其总功耗比文献[11](64.39 μW)小3个数量级。

4 结束语

本文将5/3提升小波变换和EZW编码算法应用于心电信号压缩，成本小且压缩效果良好。硬件电路可以根据信号的抖动程度自适应地调节编码精度，提升了压缩率的稳定性。通过改进了编码算法极大地降低了计算复杂度，从而节约了资源和功耗。实验结果表明：提出的算法不仅压缩性能好，且资源小、功耗低，符合便携设备面积小、功耗低的需求。