基于改进ICP算法的点云拼接方法*
杨 杰, 卢钰仁, 田 颖, 吕晓玲
(河北工业大学 机械工程学院,天津 300130)
0 引 言
点云数据的拼接配准是物体三维重建过程中最重要的环节,直接影响处理后的整体精度[1]。目前的点云拼接大多是两两拼接配准问题,最初采用的方法是顺序拼接[2],其核心思想是两两拼接,该方法简单直接,但评估点云之间的包含关系[3]和重复拼接的累积误差,会严重影响整体拼接的精度。对此,Nishino K[4]根据各个点云之间的对应关系提出了一种多视角拼接算法,但大型场景中多视角的点云数据庞大,计算点云之间的收敛十分缓慢,降低了局部点云拼接的准确性和效率。近年来,研究由局部拼接转向全局拼接。利用平差方法[5]估计全局最优坐标转换参数提高配准精度与可靠性是一种最常用的方法。
本文根据拼接中大角度变换存在的问题,提出了一种提取拼接点对的条件约束方法,在对点云数据进行粗拼接时,选取预参考点并对两组点云中对应点关系进行改进,对获取的不同帧数的点云数据进行约束条件的比较,去掉不符合条件的点云数据后,再对粗拼接数据进行精确拼接。针对本文提出的算法对室内室外场景进行实验,以验证所提出的方法的可行性。
1 点云数据粗拼接
1.1 拼接策略选取
三维几何模型的变换通常包括旋转、平移和缩放,在拼接过程中不考虑缩放,只需要求得目标点云集B到源点集A的旋转矩阵R和平移向量T,使得经过左边变换后得到的旋转矩阵(R·A+T)与目标点云集B之间的距离最小。
经典迭代最近点(iterative closest point,ICP)算法中使用的点与点的对应关系为
d=min‖X-(R·A+T)2‖
(1)
因此,经典ICP算法[6]需要对点云遍历处理,由于点云数据中法向量[7]是点云的重要参数,在拼接过程中也需要对其进行计算,所以将对应点对的关系改进为法向量之间的对应关系,即点与面的对应关系,如图1所示。
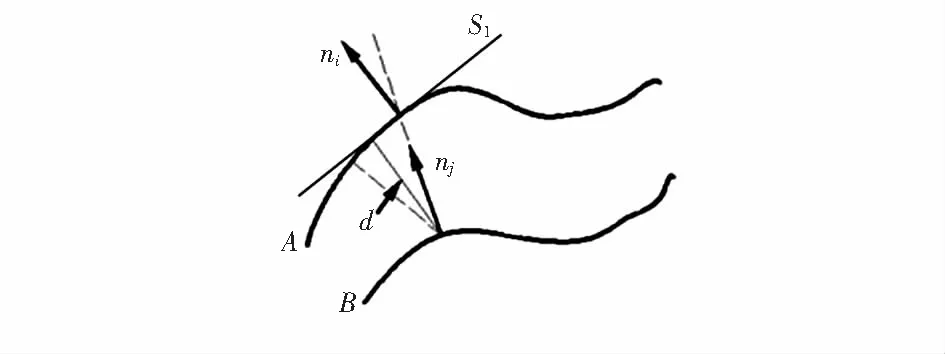
图1 点到平面距离示意
d′=min‖[X-(R·A+T)2]·ni‖
(2)
式中ni为待拼接数据点的法向量。
1.2 预参考点对选取
本文采用了对点云数据中点与其邻域点之间的法向量夹角的变化程度来评估点对之间的关系。如图2所示,若夹角变化程度大,说明该模型曲面变化复杂;若夹角变化程度小,说明模型曲面平滑。选取出点云模型中法向量变化突出的点,精简对应点对。因此,设定点云模型中某一点Pi处的法向量变化趋势即其特征变化程度为其法向量与其近邻点法向夹角的算术平均值
(3)
式中θij为点Pi的法向量与其近邻点Pj的法向量的夹角,n为比例系数。
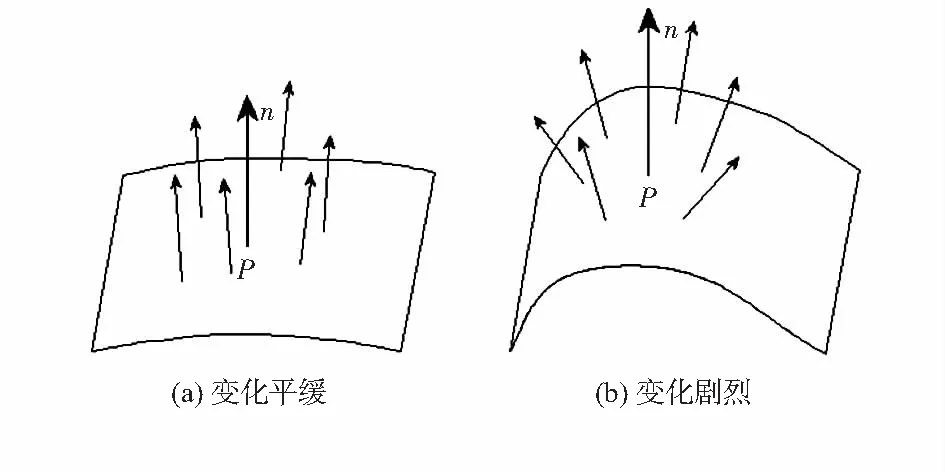
图2 不同区域的方向量示意
根据点云数据模型体积V和点数量的大小n决定取不同的σ值进行分析,如图3所示,σ取值较小时,将会对原点云模型的细节信息保存得相对完整,但局部信息去除较多;σ取值较大时,参考点集的点密度相对较大,计算保留的点较多。σ一般取5~10之间。

图3 不同σ值所对应的参考点集
获取参考点对后即可对点云数据进行拼接处理,对点云模型的粗拼接效果如图4所示,经过点云粗拼接后的两幅点云数据已经重合了很大部分。

图4 点云粗拼接效果
2 精确拼接点对获取
本文用曲率表示关键点的局部近邻域形状变化趋势,并将其作为识别点云模型特征的重要依据。
设曲面S:r=r×(u:v)在点的主方向为(d)=du:dv,若定义Kn为A点处的主曲率,则Kn一定满足[11]
(L-KnE)(N-KnG)-(M-KnF)(M-KnF)=0
(4)
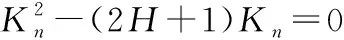
对选取的对应点对进行曲率计算,因为在计算机测量和计算时会出现不可避免的偏差,建立以下约束条件
(5)
如果点云中的Bi点不满足式(5),需要将所选点剔除,选取另外互不共线的点对继续进行比较,直至搜索完全参考点对点,找到点Ai所有可能匹配点Bi。
3 建立约束条件
1)对应点之间距离约束
若两组模型的拼接点对是正确拼接匹配点对,根据刚体不变性及实际应用情况,只需满足:|dist(xi,yi)|≈|dist(xj,yj)|。计算每个初始点对
(6)
式中δ1为设定的距离误差,若计算两点间距离满足式(6),则将点对(xj,yj)记为相对于点对(xi,yi)的符合距离约束的点对。
2)对应点的曲率约束
根据关键点的曲率值建立如下约束条件
(7)
式中δ2为给定的曲率误差。
4 点云数据精确拼接
将粗拼接后的结果作为新的初始位置,利用改进ICP算法进行精确拼接。虽然只是经过了粗拼接后,但已经得到了较好的初始位置关系,计算出的旋转矩阵R和平移矩阵T误差最小,可以得到最优变换矩阵
(8)

由于对选取点对和计算点的距离上有优化,并且对精确点对有优化和约束,所以,如表1所示,算法在点云拼接速度和精度上有所提高。
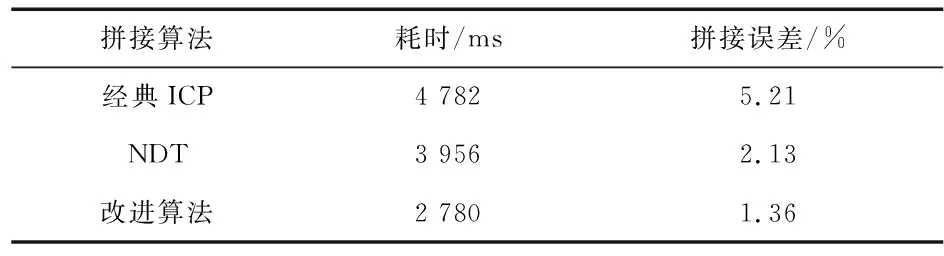
表1 不同点云拼接算法结果比较
点云精确拼接处理效果如图5所示,在粗拼接的基础上对点云数据进行精确拼接并进行点云融合。可以看出:两幅大角度的点云图像经过点云精确拼接后能完整地重现真实物体的特征。

图5 点云精确拼接示意
5 结 论
本文针对点云数据获取时,角度差异较大的数据拼接误差较大的问题,分析了两幅点云之间点与点之间的关系,提出了点到面的计算方法,并根据点的法向量的变化提取预参考点,简化了两组点云之间的计算复杂程度。对拼接点云进行优化约束,求得精确点对完成点云拼接。实验结果表明:与传统的点云拼接算法比较,本文改进的算法能够有效提升处理速度并减少了实验误差,拼接算法融合后的点云数据能够很好地达到重建的精度要求。

