基于绝热捷径快速实现远距离的四维纠缠态的制备∗
张春玲 刘文武
(阳光学院信息工程学院,福州 350015)
1 引 言
作为量子信息的一种载体,量子纠缠态一直以来都是量子信息领域的一个研究热点.近年来,学者们提出多种方案和技术用于制备量子纠缠态.其中,受激拉曼绝热技术(stimulated Raman adiabatic passage,STIRAP)[1,2]因其独有的特性而被广泛应用于量子纠缠态的制备[3−6].一般地,基于STIRAP的设计方案中,只要绝热条件能够满足,系统将处于一个本征值为0的暗态中演化,此类方案几乎不受实验参数波动性的影响,然而,为了获得高保真度的纠缠态,通常需要很长的演化时间.很显然,较长的演化时间将导致系统受消相干作用的影响,甚至使得理论方案不成立.为了克服传统绝热技术的这个弊端,绝热捷径(shortcuts to adiabatic passage,STAP)[7,8]应运而生.近几年提出了很多关于STAP的研究[9−14].其中,Berry等[14]提出的无跃迁量子驱动(transitionless quantum driving,TQD)深受追捧.此方法通过逆向构建一个反向驱动(counter-diabatic driving,CDD)哈密顿使得系统精确地沿着原始哈密顿的本征值演化.然而,一般情况下,这个哈密顿在实验上并不能实现.2015年,Chen等[15]提出了一种新的模型攻克CDD哈密顿的缺点,该方案结合大失谐和量子Zeno动力学将系统哈密顿近似等效于反向驱动哈密顿,并基于此方法快速制备了两原子Greenberger-Horne-Zeilinger态 (GHZ态).随后,Huang等[16]和Shan等[17]将此方法分别应用于多原子的W态和GHZ态的制备.相比于以上的低维纠缠态,高维纠缠态更违背了局域真实性[18],而且为很多量子信息处理提供了更高的安全等级[19]和更快的传输速度[20,21],因此被广泛应用于量子成像[22]、量子通信[23]、量子模拟[24]、量子计算[25].近几年,多维量子态在理论和实验上被广泛研究[26−29].受文献[15]启示,本文应用TQD快速实现了居于两个由光纤连接的耦合腔中的两个原子的四维纠缠态的制备.
2 理论分析
2.1 理论模型
本系统考虑两个原子分别被囚禁在两个由光纤连接的双模光学腔中.如图1所示,每个原子都有两个激发态和,两个中间态和, 和两个基态和2 表示原子序号).原子的跃迁与腔模Cij耦合,对应的耦合系数为gij,同时,原子的跃迁受拉比频率为Ωij的激光驱动,两个光学腔用一根双模光纤F连接,耦合系数为λj(j=L,R).在相互作用绘景下,系统的总哈密顿为(=1)
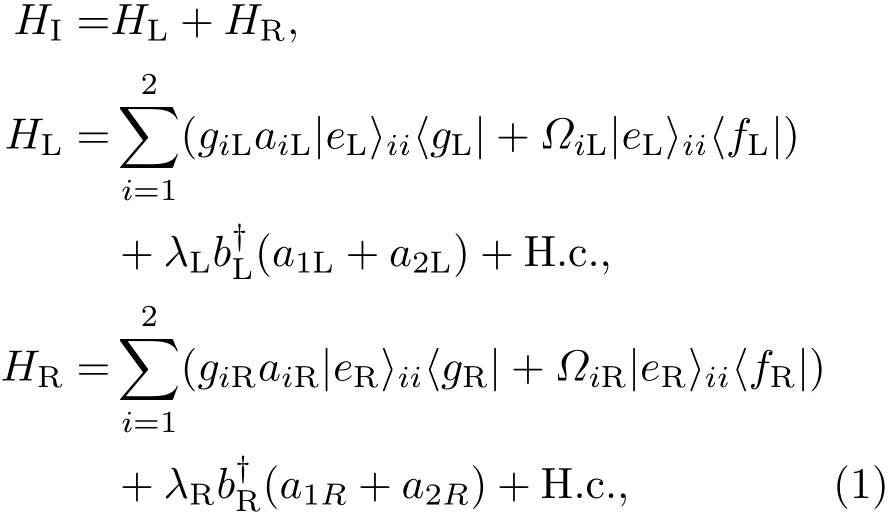
其中,a是腔模的湮灭算符,b†是光纤模的产生算符.为方便起见,设定giL=giR=g,λL=λR=λ.为了得到目标态
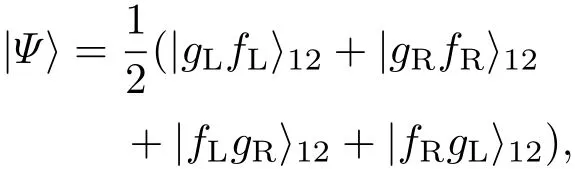
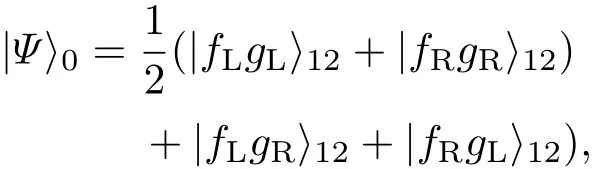

图1 实验装置图以及原子能级结构图Fig.1. The experimental set-up diagram and the atomic level configuration.
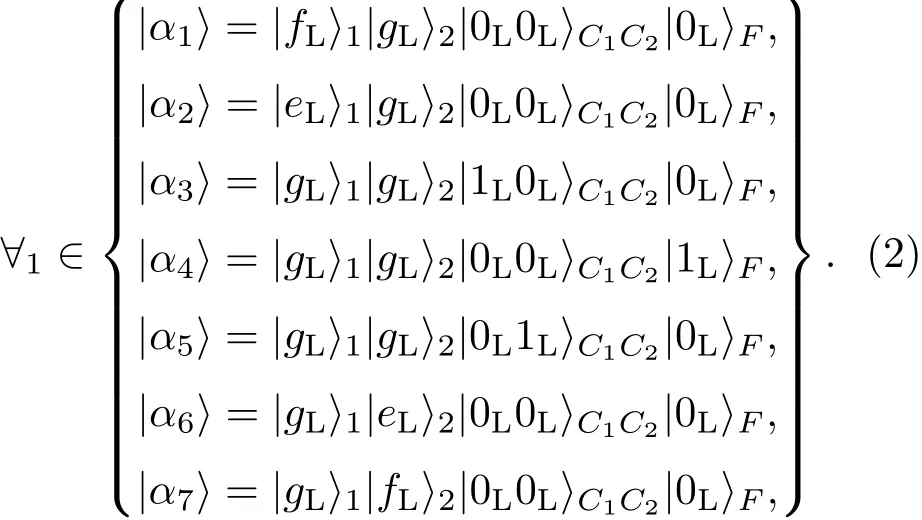
将左旋哈密顿HL分为包括腔和原子以及光纤相互作用的哈密顿,即以及原子与激光脉冲作用的哈密顿,即根据量子Zeno动力学理论[30],当g,λ≫ΩiL,左旋哈密顿HL可以等效为
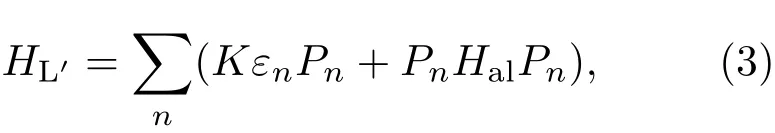
其中,K是耦合系数,εn是的本征值,Pn是的本征投影.为了获得HL′,首先计算的本征态为
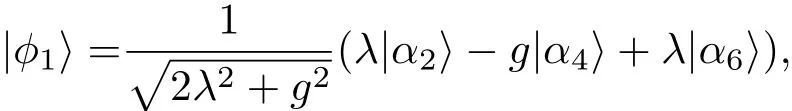

对应本征值为ε1=0,ε2=g,ε3= −g,ε4=和根据量子Zeno动力学[15,30],可得哈密顿HL′为
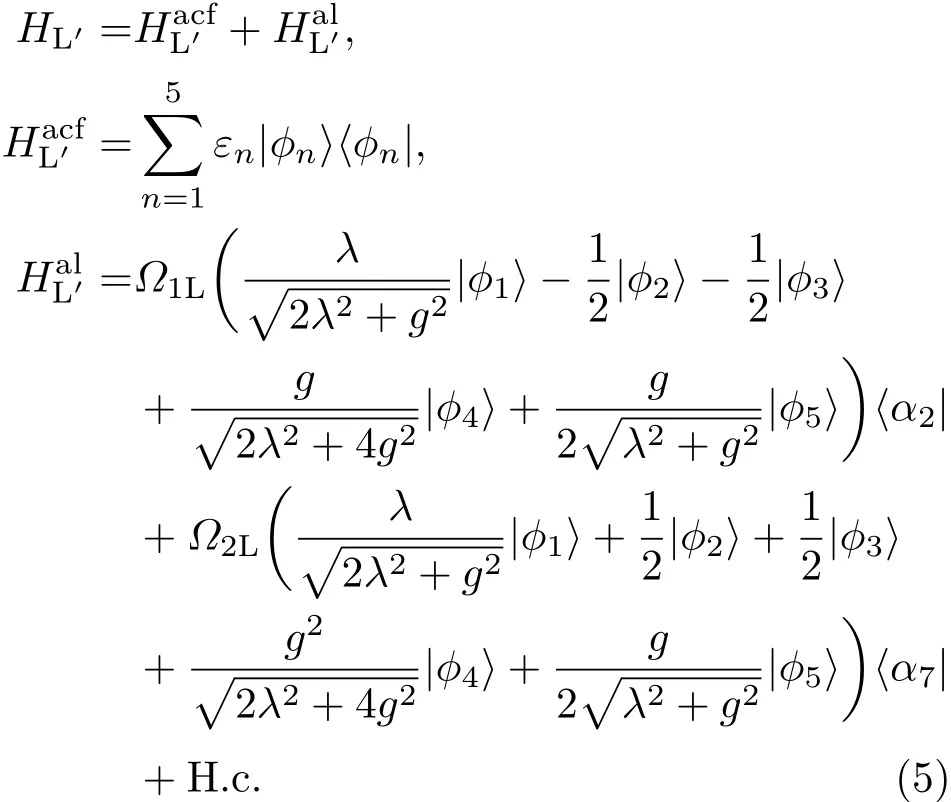
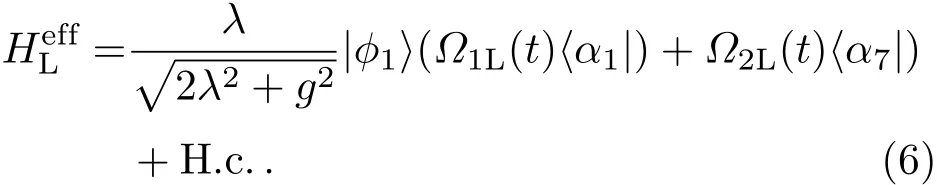
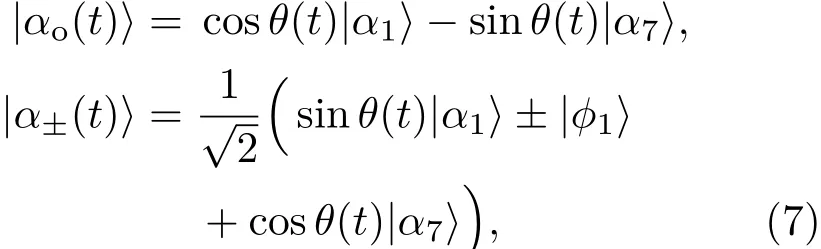
2.2 利用无跃迁量子驱动构建绝热捷径
众所周知,受激拉曼绝热过程需要较长的演化时间,这将导致系统受消相干因素的破坏,甚至使得理论结果不成立.根据Berry无跃迁量子驱动理论[14],可以求解出一个能够精确驱使系统在暗态中演化的CDD哈密顿.与哈密顿等效的最简单的CDD哈密顿可以表示为

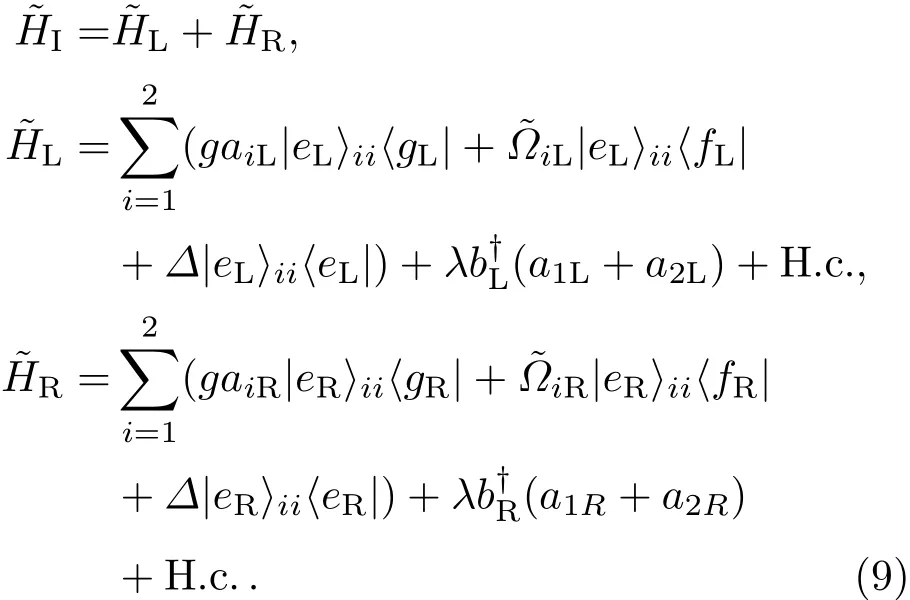
与方程(1)到方程(6)的近似方法类似,可以得到一个APF系统的有效哈密顿
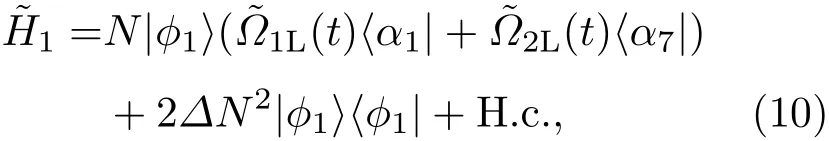

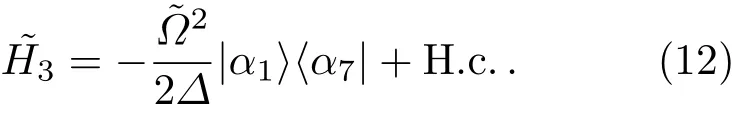
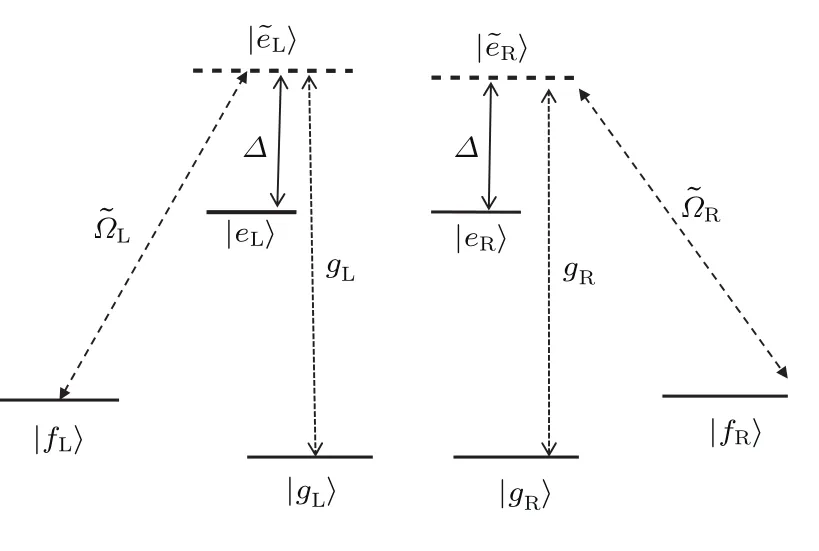
图2 APF系统的原子能级结构图Fig.2.The atomic level confguration for the APF Hamiltonian.
2.3 利用无跃迁量子驱动快速制备四维纠缠态

这里,利用高斯脉冲驱动原子,其表达式为
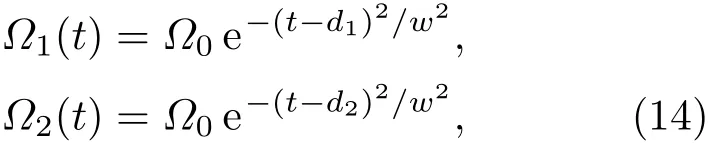
其中Ω0,di,w分别表示脉冲的峰值、时间延迟和脉宽.为了满足方程(13)的边界条件,本文选定参数Ω0=0.2g,d1=60/g,d2=30/g,w=18/g.为了凸显STAP方案的优点,图3描绘了在原始哈密顿和APF哈密顿作用下,演化进程中和的布居数. 图3(a)表明,为了实现转移利用STAP技术,演化时间只需要80/g,相比之下,如图3(b)所示,在相同的实验参数下,利用传统的STIRAP,无法实现的完美转移,为了使得系统最终布居需要改变激光脉冲参数,如图3(c)所示,此时演化时间需要达到220/g以上,将近STAP的三倍.因此,STAP大大缩短了演化时间.
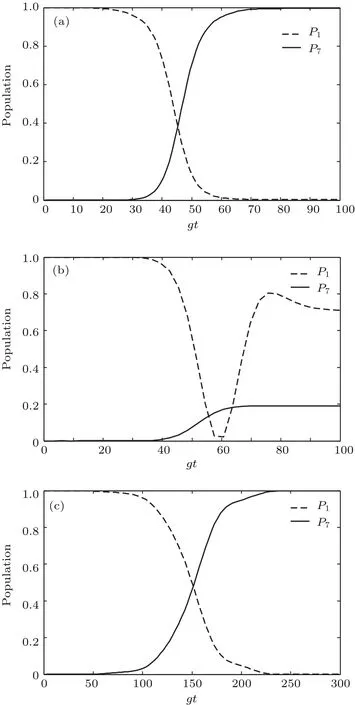
图3 |α1(P1)和|α7(P7)的布居数 (a)基于AFP系统哈密顿,其中激光脉冲参数Ω0=0.2g,d1=60/g,d2=30/g,w=18/g;(b)基于原始哈密顿,其中激光脉冲参数 Ω0=0.2g,d1=60/g,d2=30/g,w=18/g;(c)基于原始哈密顿,其中激光脉冲参数 Ω0=0.2g,d1=200/g,d2=100/g,w=80/gFig.3.The population of states|α1(P1)and|α7(P7):(a)Governed by the APF Hamiltonian˜HL via TQD,with Ω0=0.2g,d1=60/g,d2=30/g,w=18/g;(b)governed by the original Hamiltonian HLvia the adiabatic passage,with Ω0=0.2g,d1=60/g,d2=30/g,w=18/g;(c)governed by the original Hamiltonian HLvia the adiabatic passage,with Ω0=0.2g,d1=200/g,d2=100/g,w=80/g.
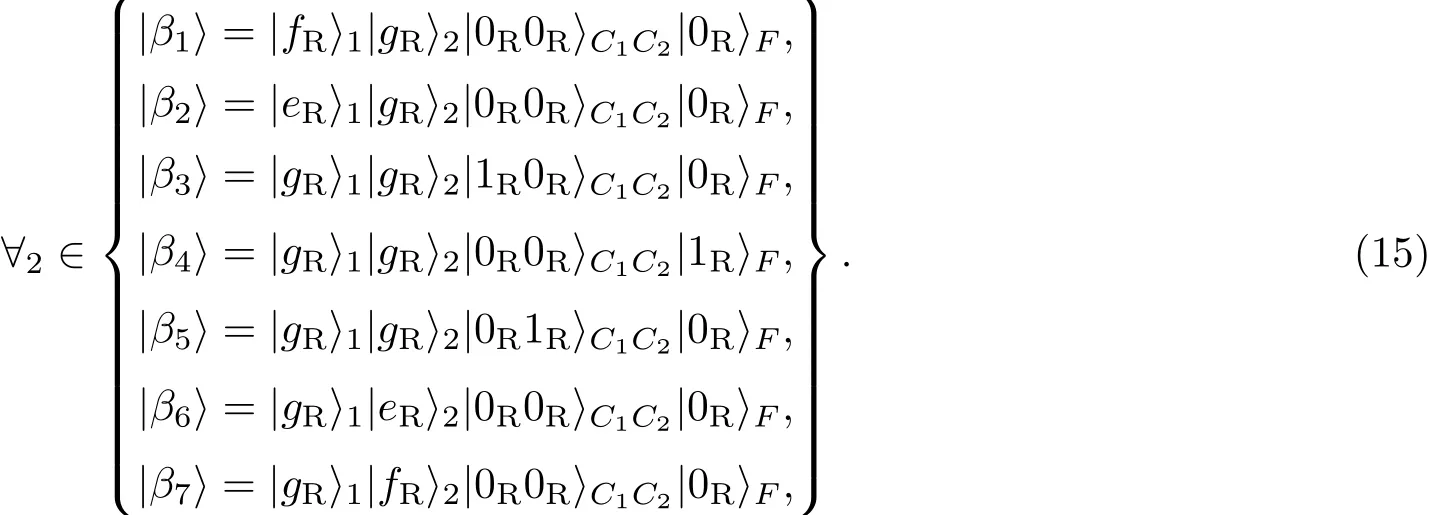

在大失谐条件下,对应的暗态可表示为
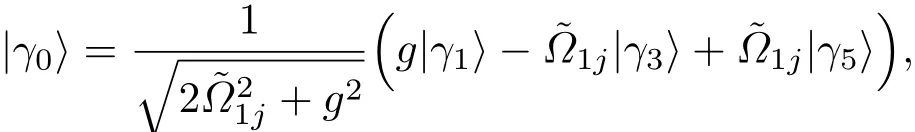

也即,制备了四维纠缠态
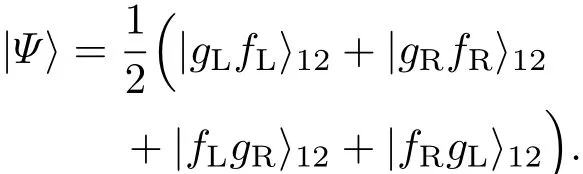
3 数值模拟与讨论
接下来,利用数值模拟说明上述结果的有效性.首先定义四维纠缠态的保真度为其中,是本文所要制备的目标态,ρ是系统演化密度算符.图4绘制了保真度和演化时间的关系,可以看出,当gt>80,保真度接近于1,同时本方案无需精确控制操作时间.
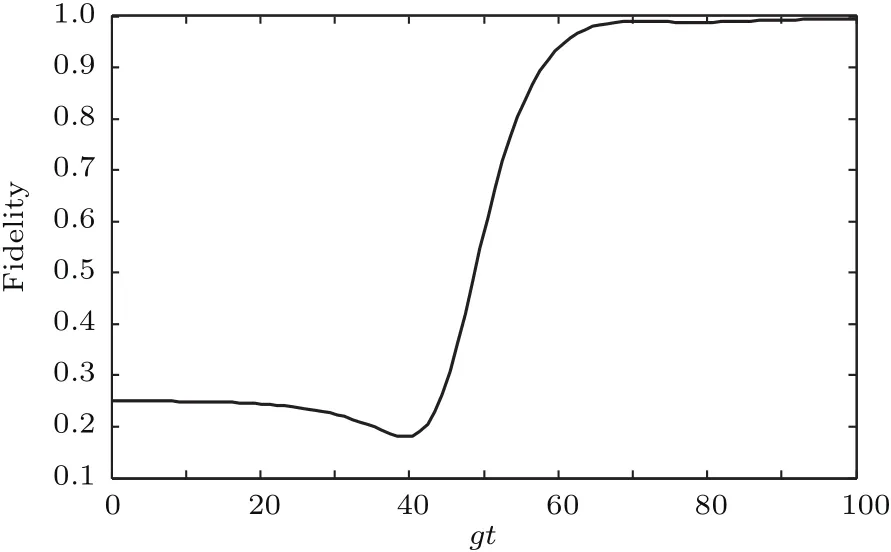
图4 四维纠缠态的保真度与无维度时间gt的关系Fig.4.The fidelity of four-dimensional entangled state versus the dimensionless parameter gt.
本文也分析了环境对纠缠态保真度的影响.本系统消相干因素主要有原子的自发辐射、腔场的衰减以及光纤的衰减.若考虑消相干因素,系统的主方程表示为

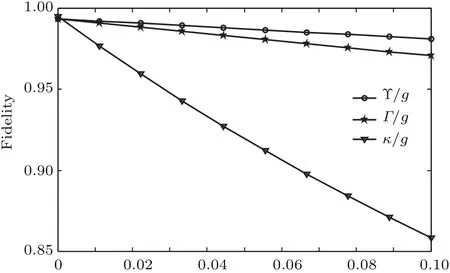
图5 四维纠缠态的保真度与原子的自发辐射、腔场的衰减以及光纤的衰减等消相干因素的关系Fig.5.The fldelity of the maximum four-dimensional entangled state versus the dissipation factor Γ , κ and Υ .
接下来简单讨论实验的可行性.本方案中六能级原子利用Rb原子[33−35]来实现,其中原子的和分别用激发态52P3/2的超精细结构能级和和分别用基态52S1/2的超精细结构能级和和分别用基态52S1/2的超精细结构能级和文献[36]指出,单个离子可以长时间地被囚禁在腔中的一个固定位置,而且可以停留很长时间.另外,文献[37]已经报道了腔和光纤的超低损耗耦合,且腔与光纤耦合效率可以达到99.9%.因此,随着腔量子电动力学技术的不断更新,本文提出的四维纠缠态的制备方案或许在不久的将来能够在实验上得以实现.
4 结 论
本文提出一种基于绝热捷径技术加快两个原子的四维纠缠态的制备,其中两原子分别被囚禁在光纤耦合的两个光学腔中.本文特点是,借助大失谐的近似来构建一个和反向驱动哈密顿等效并且在实验中可实现的系统.数值结果表明,本方案所需的演化时间远远小于基于STIRAP的方案.此外,本文还分析了包括原子自发辐射、光纤耗散、腔中光子泄漏等消相干因素对四维纠缠态保真度的影响,结果表明,采取合适的实验参数,本方案对这些因素具有很好的免疫能力.

