基于PLSR的压裂增油量变权重组合预测方法研究
李延平,修增鹏,丛 岩
(1. 东北石油大学 地球科学学院, 黑龙江 大庆 163318; 2. 大庆油田第一采油厂, 黑龙江 大庆 163318)
0 前 言
压裂作为低渗透断块油藏开发中重要的增产措施,需选取合适的分析方法和模型对增油量进行评估。伴随油井压裂后不同阶段储层渗流特征变化,影响压裂效果的主要因素权重会发生变化,对模型预测精度和可靠性产生影响。针对此类情况,经验类比法、试井资料法、统计法等传统预测方法已不能满足增油量预测和分析需求。近年来应用欧式贴近度法、模糊综合评判法及灰色关联法取得了一定的效果,最终提取的单指标或组合反映油井压裂后状态的模糊性和不确定性,对于模型信息提取与预测结果解释能力较弱[1-3]。参与建模过程中部分变量具有变化趋同的特点,解释变量必然存在多重共线性,本文提出应用偏最小二乘回归克服复杂参数建模过程中的多重共线性、高维低样本量等问题,并有效分析出不同阶段影响压裂增油量的主要因素。
本文通过油田现场压裂井实例验证该模型的有效性,将油井压裂后的增油量预测转化为基于偏最小二乘回归的变权重组合问题,结合该方法具有类似主成分分析(PCA)的特性,提取主要成分解决自变量存在多重共线性问题。该方法还提供了类似典型相关分析(CCA)的研究内容[4-5],通过变量投影重要性指标可以有效测度参数权重,根据参数相关性组合出主要影响因子,反映增油期内不同阶段主成分中主要参数权重变化规律和重要的特征信息[6],实现不同阶段各参数变权重条件下增油量拟合,为油井压裂增油量提供更为合理的预测与解释模型。
1 方法原理与计算步骤
1.1 数据标准化处理
为消除模型建立过程中不同量纲的参数对压裂预测与解释结果的影响,设自变量压裂相关参数集合X=[x1,…,xp],xjRn,因变量增油量为YRn,将变量集合进行标准化变换。记E0为X经过标准化处理后的数学矩阵,F0为Y经过标准化处理后的数学矩阵。
1.2 数学问题转化及分析过程
设t1是标准化矩阵E0的第1个成分,u1是标准化矩阵F0的第1个成分,其表达式有t1=E0w1,u1=F0c1,w1,c1为单位向量,如果要t1,u1能分别较好地代表X与Y的数据变异信息,根据主成分分析(PCA)原理,应该有t1,u1对方差贡献最大,结合典型相关分析(CCA),要求t1,u1相关度达到最大,综合上述条件,在偏最小二乘回归中,要求t1,u1的协方差cor(t1,u1)最大,相当于从自变量参数集合中提取影响压裂的主要影响因素,并兼顾此因素解释压后增油量的代表性。转化为数学问题相当于向量w1,c1经过单位化条件下,优化目标cor(t1,u1)=w1TE0TF0c1达到最大。最终归结为求矩阵E0TF0F0TE0的特征值和特征向量[7]。为了求解方便,利用拉格朗日乘子法分别对w1,c1求偏导,并两式相互代入,得到:
E0TF0F0TE0w1=λ2w1
(1)
F0TE0E0TF0c1=λ2c1
(2)
其中,w1是E0TF0F0TE0的最大特征值λ2所对应的单位特征向量,c1是F0TE0E0TF0的最大特征值λ2对应的单位特征向量,由此可见w1和c1是方差贡献和相关性的最大权衡。
1.3 建立回归方程并利用残差阵抽取成分
通过建立初始变量E0和F0对t1的回归,解决E0到F0的映射问题。回归方程标示如下:
E0=t1w1T+E1
(3)
F0=t1c1T+F1
(4)
其中,w1=E0t1/t1t1T中,c1=F0t1/t1t1T分别是回归方程E0和F0对t1的系数向量,E1,F1分别是回归方程的残差阵。
用残差阵E1和F1代替E0和F0重复以上步骤,当其反映回归方程能够解释的方差占因变量方差的百分比达到足够的精度,并且将要抽取的成分对精度影响很小时,停止成分抽取,否则继续用残差阵E1和F1分别替代E0和F0重复上述步骤,通过多次压后增油有效参数综合解释成分的抽取,结合下面介绍的积累解释系数定义抽取成分对预测模型的边际贡献,最终确定选取成分的数量。
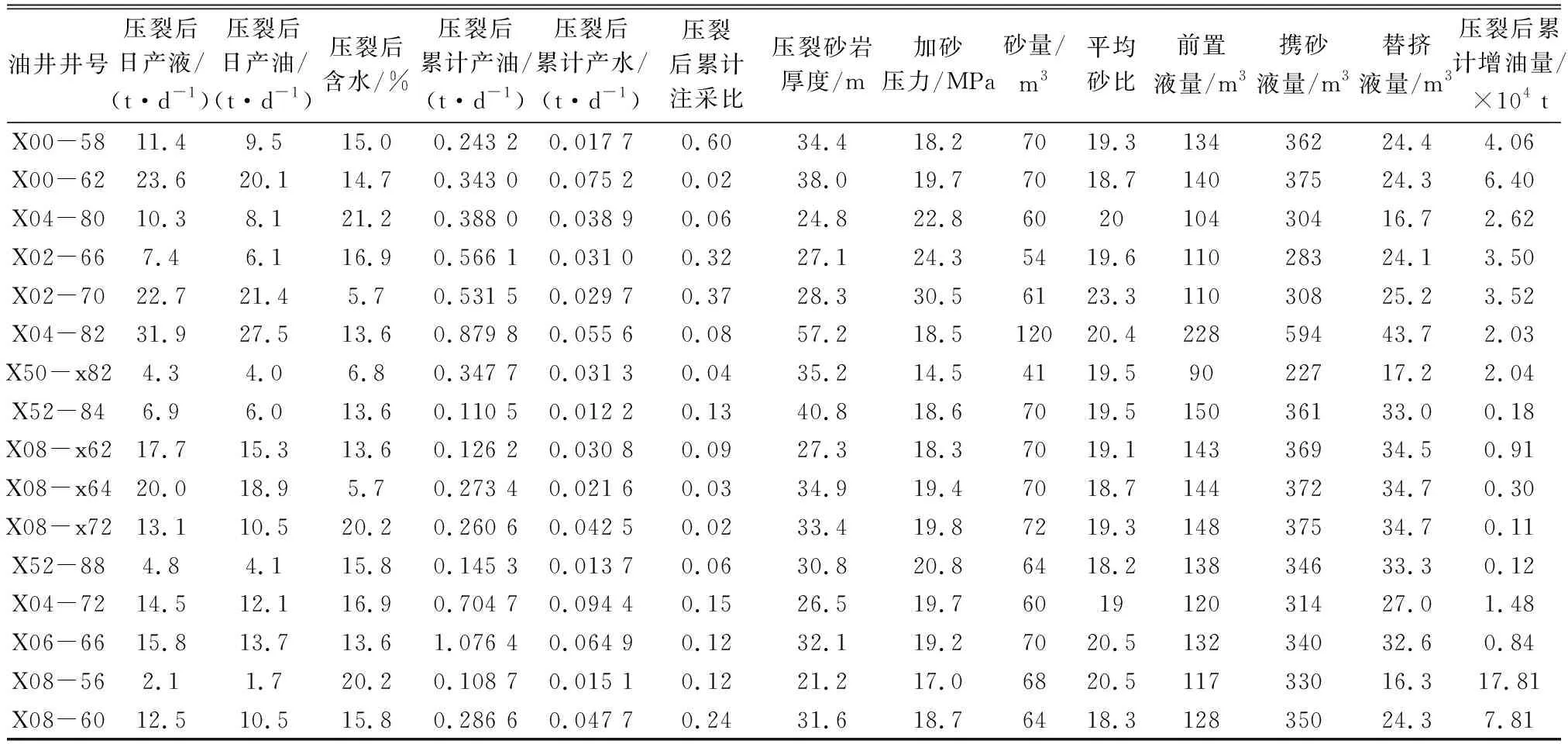
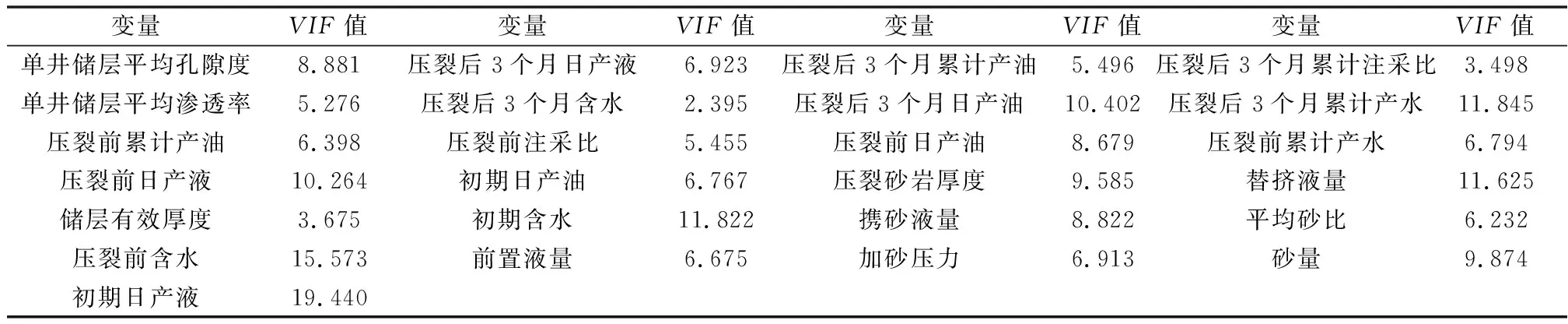
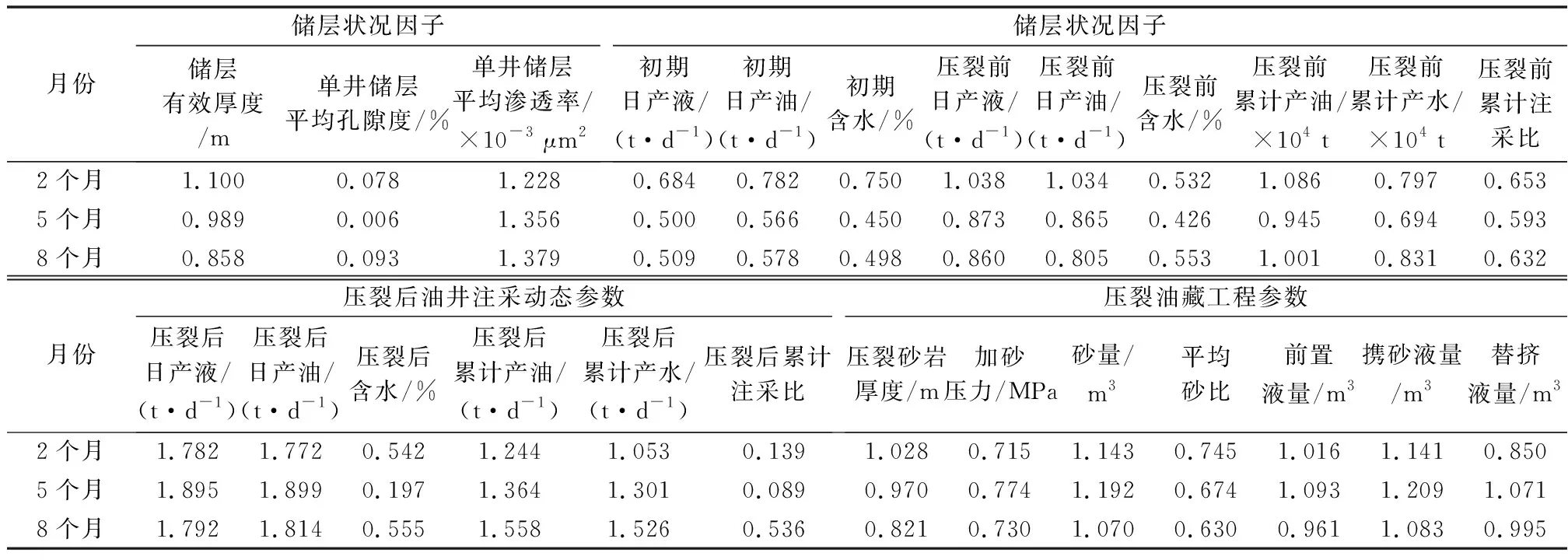
在得到成分t1,t2…,tm[m F0=r1t1+r2t2+…+r1mm+Fm (5) 其中t1,t2…,tm均为E0的线性组合,即th=Eh-1wh。 A区块为低渗透断块油藏,目前处于开发初期阶段,选取2016年10月份实施的16口压裂油井,分析油井压裂时关注的20个常用参数作为自变量,油井累计增油量作为因变量,对上述样本参数数据整理如下(见表1)。 采取方差膨胀因子法对上述数据进行多重共线性进行检测,方差膨胀因子VIFh是回归系数的估计量由于自变量的共线性使其方差增加的相对度量,对于第h个回归系数,其方差膨胀因子定义为: (6) 表1 油井压裂第4个月样本库观测参数数据 油井井号压裂后日产液/(t·d-1)压裂后日产油/(t·d-1)压裂后含水/%压裂后累计产油/(t·d-1)压裂后累计产水/(t·d-1)压裂后累计注采比压裂砂岩厚度/m加砂压力/MPa砂量/m3平均砂比前置液量/m3携砂液量/m3替挤液量/m3压裂后累计增油量/×104 tX00-5811.49.515.00.243 20.017 70.6034.418.27019.313436224.44.06X00-6223.620.114.70.343 00.075 20.0238.019.77018.714037524.36.40X04-8010.38.121.20.388 00.038 90.0624.822.8602010430416.72.62X02-667.46.116.90.566 10.031 00.3227.124.35419.611028324.13.50X02-7022.721.45.70.531 50.029 70.3728.330.56123.311030825.23.52X04-8231.927.513.60.879 80.055 60.0857.218.512020.422859443.72.03X50-x824.34.06.80.347 70.031 30.0435.214.54119.59022717.22.04X52-846.96.013.60.110 50.012 20.1340.818.67019.515036133.00.18X08-x6217.715.313.60.126 20.030 80.0927.318.37019.114336934.50.91X08-x6420.018.95.70.273 40.021 60.0334.919.47018.714437234.70.30X08-x7213.110.520.20.260 60.042 50.0233.419.87219.314837534.70.11X52-884.84.115.80.145 30.013 70.0630.820.86418.213834633.30.12X04-7214.512.116.90.704 70.094 40.1526.519.7601912031427.01.48X06-6615.813.713.61.076 40.064 90.1232.119.27020.513234032.60.84X08-562.11.720.20.108 70.015 10.1221.217.06820.511733016.317.81X08-6012.510.515.80.286 60.047 70.2431.618.76418.312835024.37.81 表2 样本库各自变量VIF值 在偏最小二乘回归计算过程中,从增油量影响变量集合X={x1,x2,…,xp}和增油量Y中依次提取出h个成分t1,t2,…,tm,所提取的自变量成分th作为综合变量,一方面尽可能地概括参数系统的主要信息,另一方面对增油量解释能力达到最大,对因变量的积累解释能力通过类似典型相关分析来定义其精度,数学表达式如下[3]: (7) (8) 式中,Rd(X;t1,…,tm)代表t1,…,tm对X的累计解释能力,Rd(Y;t1,…,tm)代表t1,…,tm对Y的累计解释能力。根据上述原理,通过Mathlab编程进行实现,各成分对X的累积解释能力和对Y的累积解释能力见表3。 表3 各成分对X的累积解释能力和对Y的累积解释能力 从表3结果来看,前2个成分累计可以解释自变量82.0%的信息,解释因变量92.4%的信息,成分1可以解释自变量79.5%的信息,解释因变量80.4%的信息,成分2对因变量整体累计解释贡献较低,对模型的预测并没有起到明显的增强作用,因此选取解释能力强的成分1作为本次回归的主要成分,本次参数系统中提取主成分解释能力符合建模预期,所携带的信息能够较好的概括原始数据特征。 通常分析和评估各参数对压裂结果的影响程度,依赖专家经验根据压后油井的征兆状态给予各参数恰当的分配权重,主观经验的局限性使得预测模型不便于推广与应用。偏最小二乘回归可以测度每个自变量xj对因变量集合Y的解释能力,其中xj对Y的解释是通过th来传递的,th作为成分可以通过变量投影重要性指标VIPj来测度,用于判断是否为成分中的主导因素,则自变量xj对Y的重要性就会被间接测度,其定义式为[9]: (9) 式中,p为成分的个数,Rd(Y;th)代表th对Y的解释能力,Rd(X;t1,…,tm)代表t1,…,tm对Y的解释能力,wAj是轴wA的第j个单位分量。 在偏最小二乘回归定义中,关注变量投影重要性指标大于1的参数,表示其在自变量解释因变量占主要作用。每个参数的变量投影重要性指标单独解释增油量预测结果是比较困难的,但相同类属的变量之间往往具有更强的相关性与特定的专业意义,将主成分中的参数归类为油藏静态地质、油田注采动态、压裂油藏工程不同专业类属反映自变量特征的主要影响因子[10],通过上述方法可以有效的压缩解释变量空间,增强信息的综合能力。建模过程中不仅要指出在庞杂的自变量系统中起主导性作用的因素,也要结合低渗透油藏压裂开发渗流理论对预测结果的指导作用。压裂后油井开发分为如下阶段:一是线性流阶段,即原油从支撑缝前缘通过高导流向井筒;二是拟径向流阶段,即原油从支撑缝前缘已降低的高导流裂缝和裂缝两侧岩石中流入井筒,截至目前该断块油井仍处于增油阶段[11],暂不做第三阶段的讨论。参与预测的参数权重伴随近井地带储层渗流特征发生不同程度的改变,以下是不同月份下样本主成分中不同参数VIPj值的变化情况(表4)。 表4 不同月份样本主成分中变量投影重要性指标 通过上述数据可知,参与回归的变量投影重要性指标随时间变化,结合储层压裂渗流机理,分析油井压裂后各阶段主成分中主要影响因子各月份累计解释占比情况(图1)。其中储层状况因子和压裂后油井生产动态因子对压裂增油量累计解释占比较大。结合变量投影重要性指标数据,第16个月开始,储层状况因子中有效厚度参数影响逐渐变小,单井储层平均渗透率影响显著增加,压裂初期随着压裂缝条数增加,主要渗流通道为导流能力强的压裂缝,其导流能力远大于储层自身孔隙,随着裂缝逐渐闭合,油井周围渗流阻力逐渐增大,储层物性对渗流影响重新凸显作用。压裂前油井生产动态因子对增油量影响随时间推移曲线形态呈“凹”形,由于压裂改造因素参与,导致累计解释占比下降,第14个月开始,其累计解释占比逐渐回升,原因在于压裂前油井的生产动态参数很大程度上反映了井控范围内油井的生产能力及储层物质基础。压裂后油井生产动态因子始终与增油量密切相关,在4种主要因子中累计解释占比始终最高,随着渗流关系的改变,压裂对储层的改造及初期油井的生产状况作为后期增油的重要因素导致其累计解释占比下降,最终初期油井的生产条件和压裂对储层的改造程度决定增油量,后期累计产水量参数变量投影重要性指标逐渐升高,说明对增油量影响显著增加,与油井含水率关联程度较高。压裂施工参数因子整体占比较高且曲线波动不大,压裂砂岩的厚度、实际加砂量、前置和携砂液量始终起重要作用但变化相对稳定。 图1 压裂主要影响因子累计解释占比图 以压裂后第16个月做为分界点,根据不同阶段主要影响因素变化特征采取分段回归方式,将标准化变量还原为原变量,建立适用于该断块的压裂增油量预测模型: Y1=-3 464.45+5.836 4xeffethic-5.076 7xporo+24.921 8xperm+…+2.585 6xlead volu+1.424 4xcarr flui+9.737xcumu wat0≤t≤t0 (10) Y2=-3 902.76+6.237 3xeffethic+4.425 3xporo+0.205 5xperm+…+2.206 7xlead volu+1.395 9xcarr flui+9.179 3xcumu watt>t0 (11) 式中,t0为第16个月;xeffethic为储层有效厚度,m;xporo为单井储层平均孔隙度,%;xperm为单井储层平均渗透率,10-3μm2;xlead volu为前置液量,m3;xcarr flui为携砂液量,m3;xcumu wat为挤替液量,m3。 通过已实施的同批次未计入本次回归的压裂井实际生产数据验证模型的可靠性,结果表明,模型预测精度在误差范围之内,可用于压裂井增油量评估,通过上述所用模型分析压裂不同阶段参数变化规律,表明此建模方法可用于不同断块的压裂增油量预测(见表5)。 1)偏最小二乘回归可以提供类似于主成分分析和典型相关分析的研究内容,选出解释能力强的主成分,可以有效消除样本参数存在的多重共线性造成的模型失真问题,根据参数的相关性组合出综合影响因子随时间的变化规律,对压裂后不同阶段转变的关键点进行界定,实现油井压裂增油期不同阶段各参数变权重条件下增油量预测。 表5 实际增油量与PLSR预测结果对比表 2)建立组合模型进行压裂增油量,可以大幅度地降低模型建构的复杂性,结合压裂渗流理论,提高了模型预测的解释能力,建立该断块的压裂增油量预测图版,把握各个阶段中综合影响因子的变化特点,优化后期措施调整时机,有针对性的进行压后跟踪与调整工作,提高增油效果。2 案例分析
2.1 基础参数数据分析
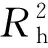

2.2 提取主成分并进行成分精度分析

2.3 压裂增油量主要影响因子分析

2.4 压裂增油量预测模型建立及对比检验
3 结 论