反比例函数中经典例题解析
我们在解决反比例函数y=[kx](k≠0)中面积类问题时,通常会过反比例函数图像上任意一点向x轴(或y轴)作垂线,那么垂足、原点和已知点三点构成的三角形面积恒等于[k2].如果反比例函数图像上依次出现A、B两点,我们将如何处理与面积有关的问题呢?今天就两个经典例题,跟大家分享一下解题技巧.
【例1】如图1,在以O为原点的平面直角坐标系中,矩形OABC的两边OC,OA分别在x轴、y轴的正半轴上,反比例函数y=[kx](k>0)的图像与AB相交于点D,与BC相交于点E.若BD=3AD,且△ODE的面积为9,则k的值为 .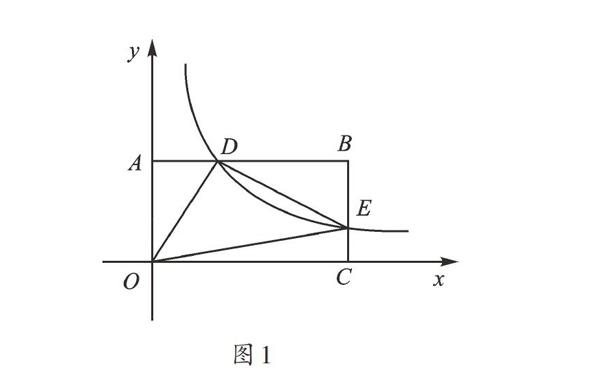
方法一:设点D(a,b),由于A、D、B三点在同一条直线上,且所在直线垂直于y轴,所以A、D、B三点的纵坐标都相同,从左至右各点坐标可以分别是:A(0,b),D(a,b),B(4a,b).
由于点B、E、C三点在同一条直线上,且所在直线垂直于x轴,故B、E、C三点的横坐标相同,都是4a.因为点D、E都在反比例函数y=[kx]的图像上,所以点D、E的横坐标与纵坐标的乘积为定值k,且点E的横坐标是点D横坐标的4倍,故点E的纵坐标是点D纵坐标的[14].由点D(a,b)可得点E(4a,[14]b),从上至下各点坐标分别是:B(4a,b),E(4a,[14]b),C(4a,0).
由各点坐标可以得出:
OA=b,AD=a,DB=3a,BE=[34b],EC=[14b],OC=4a.
S△ODE=S矩形OABC–S△AOD–S△OCE–S△DBE
=4a×b[-a×b2-4a×14b2-3a×34b2]=[15ab8].
∵S△ODE=9,∴[15ab8]=9,∴ab=[245].
∵点D(a,b)是反比例函数y=[kx]的图像上的一点,∴k=ab=[245].
方法二:设点D(m,[km]),利用方法一的推理,可得出点A(0,[km]),D(m,[km]),B(4m,[km]),E(4m,[k4m]),C(4m,0).
由各点坐标可以推出:
OA=[km],AD=m,DB=3m,BE=[3k4m],CE=[k4m],OC=4m.
S△ODE=S矩形OABC–S△AOD–S△OCE–S△DBE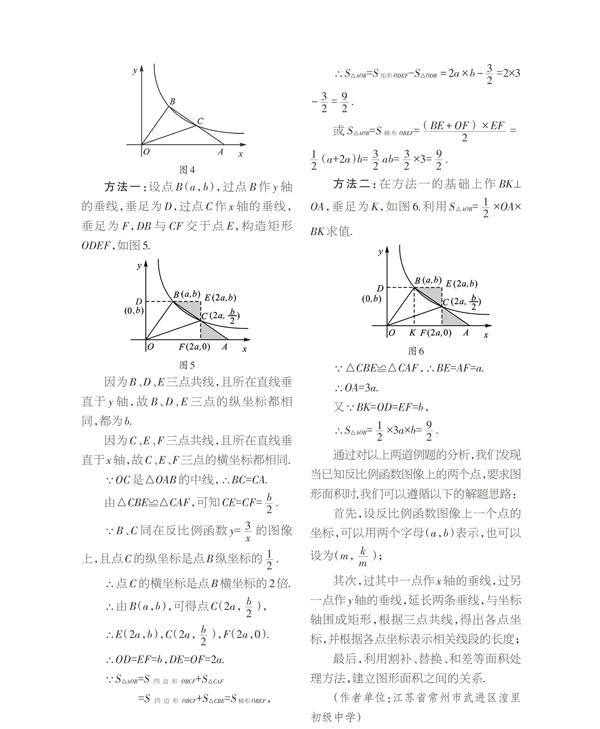
=4m×[km-k2-k2-3m×3k4m2]
=4k-k-[98]k
=[158]k.
∵S△ODE=9,∴[158]k=9,∴k=[245].
方法一中:通过点D的坐标(a,b),表示其余各点坐标以及各条线段的长度,简单清晰,既便于表示,又便于计算.
方法二中:借助一个参数字母m以及k来表示各点坐标和各线段的长度,由于分母中带有字母,所以在表示和计算时易出错和混淆,但这种方法的优点是可以直接列出关于k的方程.
【例2】如图4,在平面直角坐标系中,△OAB的顶点A在x轴的正半轴上,OC是△OAB的中线.点B、C在反比例函数y=[3x](x>0)的图像上,则△OAB的面积等于 .
方法一:设点B(a,b),过点B作y轴的垂线,垂足为D,过点C作x轴的垂线,垂足为F,DB与CF交于点E,构造矩形ODEF,如图5.
因为B、D、E三点共线,且所在直线垂直于y轴,故B、D、E三点的纵坐标都相同,都为b.
因為C、E、F三点共线,且所在直线垂直于x轴,故C、E、F三点的横坐标都相同.
∵OC是△OAB的中线,∴BC=CA.
由△CBE≌△CAF,可知CE=CF=[b2].
∵B、C同在反比例函数y=[3x]的图像上,且点C的纵坐标是点B纵坐标的[12].
∴点C的横坐标是点B横坐标的2倍.
∴由B(a,b),可得点C(2a,[b2]),
∴E(2a,b),C(2a,[b2]),F(2a,0).
∴OD=EF=b,DE=OF=2a.
∵S△AOB=S四边形OBCF+S△CAF
=S四边形OBCF+S△CBE=S梯形OBEF,
∴S△AOB=S矩形ODEF-S△ODB[=2a×b-32]=2×3
[-32]=[92].
或S△AOB=S梯形OBEF=[(BE+OF)×EF2]=
[12](a+2a)b=[32]ab=[32]×3=[92].
方法二:在方法一的基础上作BK⊥OA,垂足为K,如图6.利用S△AOB=[12]×OA×BK求值.
图6
∵△CBE≌△CAF,∴BE=AF=a.
∴OA=3a.
又∵BK=OD=EF=b,
∴S△AOB=[12]×3a×b=[92].
通过对以上两道例题的分析,我们发现当已知反比例函数图像上的两个点,要求图形面积时,我们可以遵循以下的解题思路:
首先,设反比例函数图像上一个点的坐标,可以用两个字母(a,b)表示,也可以设为(m,[km]);
其次,过其中一点作x轴的垂线,过另一点作y轴的垂线,延长两条垂线,与坐标轴围成矩形,根据三点共线,得出各点坐标,并根据各点坐标表示相关线段的长度;
最后,利用割补、替换、和差等面积处理方法,建立图形面积之间的关系.
(作者单位:江苏省常州市武进区湟里初级中学)

