一类摩擦振子黏滑周期解及其控制

袁路奇 李群宏 欧玉芹

(广西大学数学与信息科学学院， 南宁 530004)

摩擦广泛存在于生产生活当中，描述含干摩擦的振动系统微分方程的运动轨线在其相空间上是不连续的，因此求解较为困难。 Kim等人运用谐波法对一类经典库仑摩擦质量弹簧系统进行研究[1]。Csernák 等人对简谐激励摩擦振子进行研究，并在滑动状态下进行近似求解和数值仿真[2]。李群宏等人分析了Stribeck(斯特里贝克)系数模型,并对几种滑动分岔进行研究，给出传送带速度和摩擦力对振子动力学行为的影响[3-4]。白鸿柏等人对摩擦因数依赖速度的振动系统提出Fourier(傅里叶)级数算法[5]。赵旖旎等人给出含干摩擦耦合制动系统的振动分析[6]。刘丽兰等人研究可变法向力对黏滞运动的影响[7]。

本次研究中，首先引入依赖速度的分段非线性干摩擦力函数模型。由于摩擦力的非线性使得求解黏滑振动封闭解比较困难，由近似解析解分析参数变化对黏滞滑动的影响显得比较重要,从而考虑在1个周期内对黏滞和滑动2个阶段分别求解。其次,引入了控制理论。与以往文献[8-11]给出直接附加正压力或者激励不同，本次研究分别在2个方向上施加了作用力，可避免黏滞及其颤振运动。最后，通过数值仿真给出验证结果。

1 黏滞滑动的近似解析解

1.1 模型建立

建立单自由度干摩擦振动系统模型(见图1)。质量为M的振子与弹性系数为K的弹簧连接于固定壁面，传送带的速度为V0,系统的微分方程为：

(1)

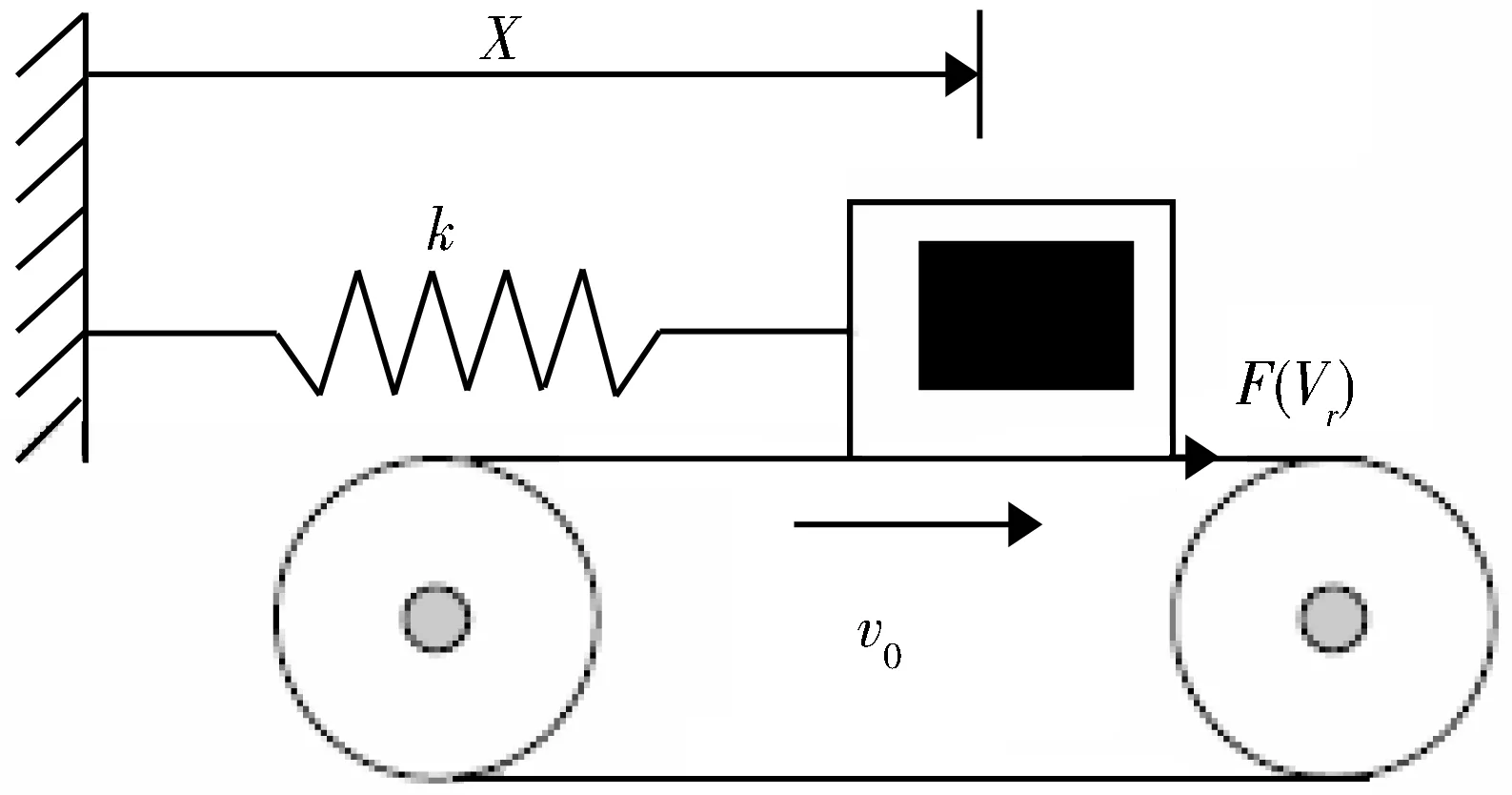
图1 单自由度干摩擦振动系统模型

其中F是依赖速度型摩擦力函数：

(2)

引入变量x(t)代替X(t)：

x(t)=X(t)-F(V0)

(3)

则方程(1)变换为：

(4)

对式(4)进行泰勒展开，并略去高阶项：

(5)

其中

所以式(4)化为式(6)：

(6)

于是，定义：

(7)

则式(6)化为式(8)、(9)：

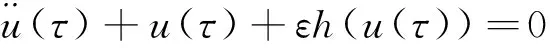
(8)

(9)

其中

1.2 求解

在纯滑动状态下，类似系统的近似解已有文献给出。本次研究则分别在黏滞与滑动状态(见图2)下进行计算，并最终给出系统的近似解析解。

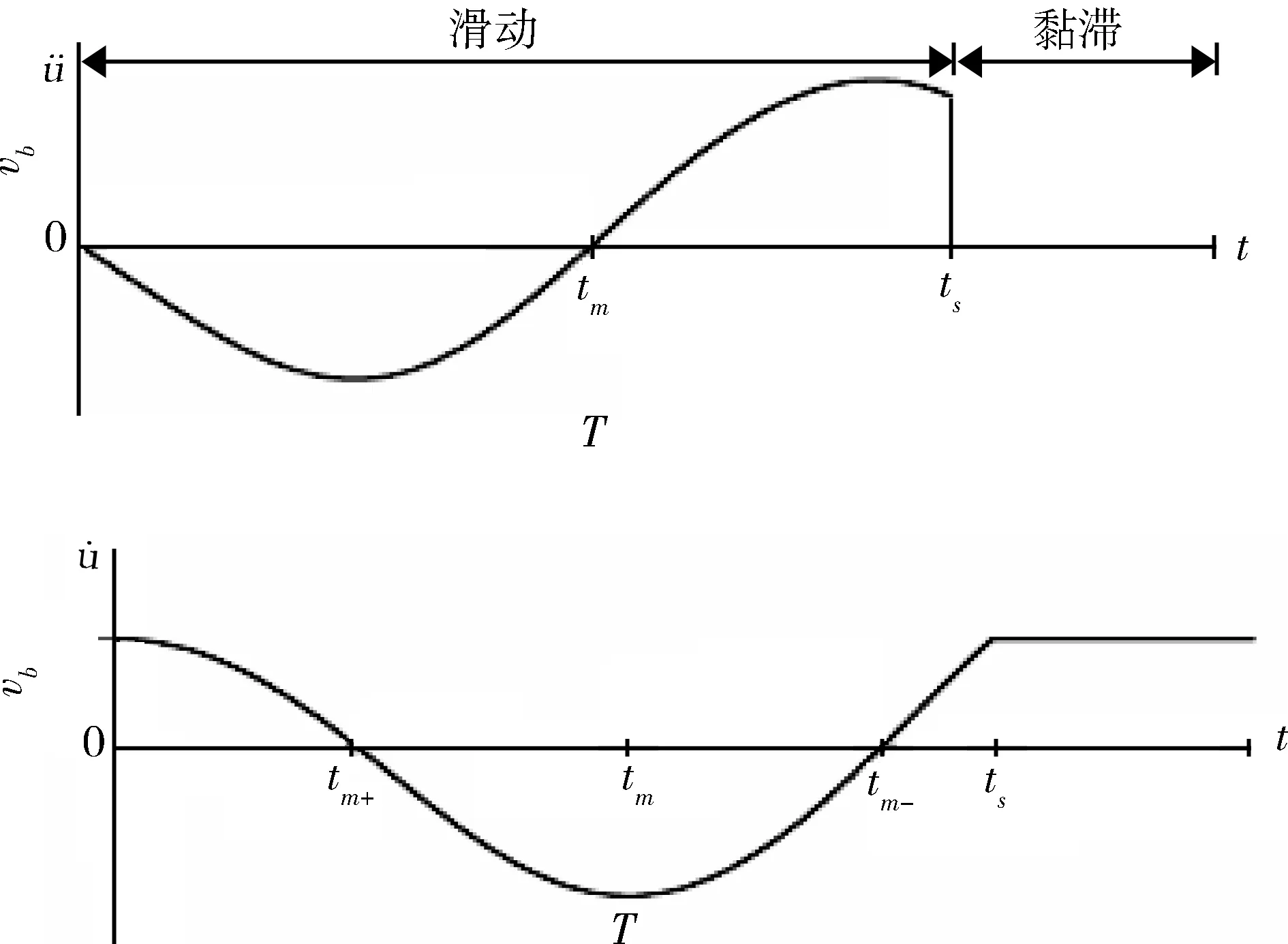
图2 黏滞与滑动状态示意图

1.2.1 滑动阶段

考虑初始时间为t=0，此时对于整个运动来说，滑动开始，黏滞结束。

(10)

采用一阶近似方法求解式(11)：

u(t)=u0(t)+εu1(t)，t∈[0,ts]，ε≪1

(11)

将式(8)、(9)代入式(11)，且当t=0时，得：

(12)

由式(8)、(10)得:

(13)

又由式(11)得:

(14)

取u1(t)的一阶近似解:

u1(t)=c1(t)cost+c2(t)sint

(15)

(16)

(17)

对式(17)进行求导：

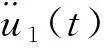
(18)

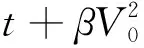
(19)

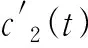
(20)

解得：

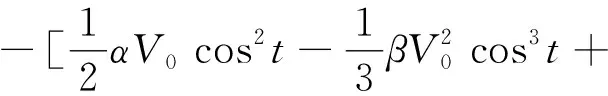
(21)

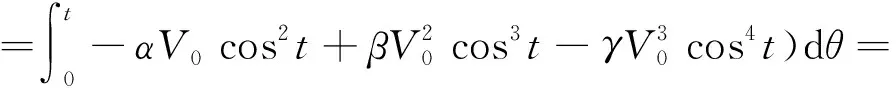
(22)

则

u(t)=u0(t)+ε[c1(t)+c2(t)+Ο(ε2)]t∈[t,T]

(23)

滑动停止黏滞开始的时间记为ts，下面求解ts：

(24)

根据式(1)得一阶近似解：

u0=v0sint

(25)

则由式(24)、(25)得：

v0costs=v0

(26)

针对式(22)对应定义域附近某一点进行泰勒展开，又ts∈[π,2π]，则在此区间中点处展开：

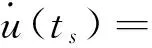
(27)

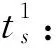
(28)

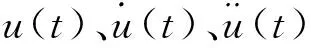
(29)

由式(22)及式(28)，即可得到滑动阶段的解。

1.2.2 黏滞状态

易知振子的滑动运动在t=ts时终止，并开始黏滞运动，则有：

(30)

u(t)=u(ts)+v0(t-ts)，t∈[0,T]

(31)

设系统振子1个完整的黏滞滑动周期为T，则：

(32)

1.3 数值仿真

首先对原系统进行仿真，取系统参数δ=0，γ=3，V0=1.24，系统初值为(0.2,0.1),利用Matlab计算并给出原系统的输出相图(见图3)。

图3 原系统的输出相图

2 黏滑运动的控制

2.1 控制策略

常见的消除或者抑制黏滞运动的方法主要有3种：(1)增加额外的阻尼补偿由摩擦特性诱导效应[8-9]；(2)增加外激励破坏黏滞滑动的极限环[10]；(3)增加法方向的压力消除黏滞滑动运动的颤振运动[11]。

采用第3种方法，与文献[11]直接施加法方向作用力不同的是，控制函数采用与速度相关的控制率消除黏滞滑动运动。

控制方程为：

(33)

(34)

令

(35)

则对应系统的状态方程为：

F(x1,x2)=

(36)

因此，系统的平衡点X0为：

由平衡点坐标知，通过调节控制律可以改变振子的最终位置。

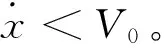
又有：

(37)

故系统的雅可比矩阵可写为以下形式：

(38)

(39)

平衡点处的特征方程为：

(40)

根据Routh-Hurwitz稳定性判定定理，若所有特征值的实部均小于零，需要满足式(41)：

(41)

2.2 控制的数值验证

取系统参数δ=0，γ=3，V0=1.24，k=1，N=1系统初值为(0.2,0.1),利用Matlab计算并给出施加控制后系统的输出相图(见图4)。

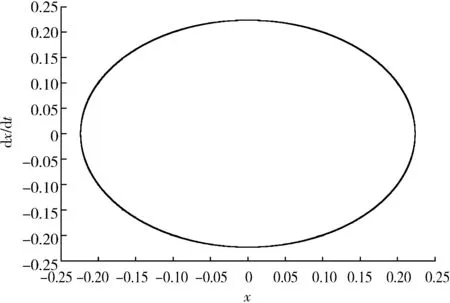
图4 施加控制后系统的输出相图

通过理论分析数值仿真验证可知，在施加控制之后成功地避免了黏滞运动。与文献[11]相比，其优点在于控制率简单容易实现，并且控制之后仍然是一个周期运动，而缺点在于在系统进入稳态之后还需要进行能量的输入。

3 结 语

考虑一类分段非线性摩擦力函数，通过近似计算分别得到在黏滞和滑动状态下的解析解并由Matlab给出数值解。设计控制函数，分别在原系统法方向和切方向施加作用力，给出在系统加载控制后在稳定状态下的参数取值范围。由数值分析结果证实，此控制方法可行，可避免黏滞及其颤振运动，并将运动稳定在纯滑动运动状态。