基于DEA模型的西南地区高校科技经费绩效评价
李 雪
(重庆师范大学数学科学学院, 重庆 401331)
近年来,随着我国高校科研经费投入的不断增加,科研成果数量显著上升。但与此同时,高校科研管理工作面临巨大的挑战,经费大量浪费、使用混乱等问题逐渐突出。为了提高科研管理效率,研究人员推出了一系列科学评价方法来衡量科技经费绩效,如平衡计分卡方法[1]、数据包络(DEA)法[2]等。本次研究采用加入虚拟决策单元后的DEA评价法,对西南地区5省(市、自治区)高校科技经费绩效进行排序,并针对科研经费管理提出了合理的建议。
1 确定高校科技经费绩效评价指标
建立高校科技经费绩效评价指标基本框架,将评价指标分为投入指标和产出指标[3],这2类指标可直接反映评价结果。投入指标包括科技经费拨入金额(万元)、科技经费支出金额(万元)、科技人力投入(人)等。产出指标包括出版科技著作数(部)、发表科技论文数(篇)、国家项目通过验收数(项)、专利数(项)、技术转让合同数(项)、科技成果获奖数(项)等。
确定上述指标之后,结合DEA评价方法,建立高校科技经费评价体系(见图1)。
2 建立DEA评价模型
2.1 DEA评价模型——C 2R模型
设有n个待评价方案,将第j个待评价方案称为决策单元Dj,Dj(1≤j≤n)的输入、输出向量分别为:
xj=(x1j,x2j,…,xmj)T>0,j=1,2,3,…,n
yj=(y1j,y2j,…,ysj)T>0,j=1,2,3,…,n
有:xij>0,yrj>0,i=1,2,3,…,m,r= 1,2,3,…,s。 其中,xij为第j个决策单元对第i种类型输入的投入量;yrj为第j个决策单元对第r种类型输出的产出量[4]。

图1 高校科技经费评价体系
然后在后续计算过程中赋予输入的投入量、输出的产出量以恰当的权重(见图2)。
投入量n个决策单元决策单元Dj对应效率评价指数hj:

v=(v1,v2,…,vm)T
u=(u1,u2,…,us)T
经过Charnes-Cooper变化,可以将C2R模型变换成线性规划模型——P模型:

若最优解hj0=1,则该决策为DEA相对有效;若w、μ中有一个为0,则该决策为DEA弱有效;若hj0≠1,则称该决策为DEA非有效。
2.2 改进后的DEA评价模型
在实际运用中,通过上述DEA模型只能判断决策单元Dj是DEA相对有效或是DEA非有效。而当
决策单元是DEA相对有效时,无法确定排序,也就达不到评价的最终目的[5]。引进虚拟决策单元,令
(i=1,2,3,…,m,r=1,2,3,…,s)
xn+1=(x1,x2,…,xm)T
yn+1=(y1,y2,…,ys)T
则改进后的模型为:
3 西南地区高校科技经费绩效分析
利用DEA评价方法对我国西南地区2016年高校科技经费绩效进行评价,采用的数据来自《2016年高等学校科技统计资料汇编》(见表1)[6]。

表1 2016年西南地区高校科技经汇总情况
通过DEA的辅助软件 —— Matlab进行计算与分析[7]。分别应用原模型和改进后的模型对5个地区的经费绩效数据进行评价(见图3),最终得到评价结果(见表2)。
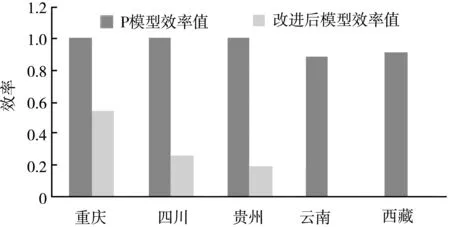
图3 模型结果对比图

省(市、自治区)P模型效率值改进后模型效率值重庆1.000 00.546 4四川1.000 00.265 0贵州1.000 00.198 3云南0.991 3—西藏0.999 4—
从图3和表2可以看出,由C2R模型中的P模型计算出大部分地区的效率值为1,可知西南地区高校科技经费的绩效显著。同时,P模型评价结果显示,重庆、四川、贵州的科技经费绩效为DEA有效,而云南和西藏的高校科技经费绩效为DEA非有效,其绩效值分别为0.991 3、0.999 4。我们可以得知云南高校科技经费绩效比西藏的高,但无法据此对DEA有效的区域进行排序。在加入虚拟决策单元改进模型后的评价结果显示,重庆、四川、贵州的高校科技经费绩效值依次为0.546 4、0.265 0、0.198 3。因此,最终的绩效排序由高到低为重庆、四川、贵州、西藏、云南。
4 结 语
C2R模型中的P模型和改进后的模型评价结果有较大区别,很明显,改进后的模型能对高校绩效实现全面排序。对于高校科技经费绩效偏低的地区,应该加强管理并予以重视,寻找效率偏低原因,并制定科学的管理制度。对于绩效偏高的地区,有关部门应该制定相应的奖励机制,增强高校科技创新热度。
--западе Китая

