考虑出行者损失厌恶的后悔随机用户均衡模型

赵 磊，关宏志*，张新洁，赵鹏飞

(北京工业大学a.建筑工程学院；b.交通工程北京市重点实验室，北京100124)

0 引言

合理的路径选择行为假设，对准确预测城市交通网络流量分布具有重要作用.1952年，Wardrop[1]提出了遵循最短路径择路机制的用户均衡(User Equilibrium,UE)模型.后来人们发现，实现该机制需要假设出行者是完全理性的，拥有完全的交通网络信息，而且忽略出行者的偏好差异和认知的有限性，这就有悖于现实生活中人们表现出的有限理性行为.因此，最短路径机制受到了一些学者的质疑[2-4].Daganzo等[5]针对出行者认知能力的有限性，进一步提出了随机用户均衡(Stochastic User Equilibrium,SUE)模型，随后的路径选择研究大多都是在UE和SUE这两种模型的基础上展开的.

针对随机效用最大化(Random Utility Maximization,RUM)方法的缺陷，如完全理性假设和IIA(Independence of Irrelevant Alternatives,IIA)特性等，Chorus[6]提出了随机后悔最小化(Random Regret Minimization,RRM)模型.后悔被认为是一种负面情绪，发生在决策者意识到其他备选方案比考虑方案表现得更好的情况下；反之，当决策者发现考虑方案性能更好，决策者会产生欣喜的情绪.而后，Chorus[7]进一步完善了RRM模型的构建，提出了一个新的RRM模型，该模型随后被当作是经典的RRM模型.经典的RRM模型用一个对数和的方法替代两个最大值运算，这样使得后悔函数成为一个光滑、关于属性差单调递增的连续函数.RRM模型假定出行者在出行选择决策中，总是倾向于选择预期后悔最小的备选方案.随后，Chorus等[8]和Chrous[9]继续改进了RRM模型，并分别提出了混合的RUM-RRM模型和一般化的随机后悔最小化(Generalized Random Regret Minimization,GRRM)模型.Van Cranenburgh等[10]从新的视角对经典的RRM模型展开分析，指出该模型中的偏好参数不仅反映了属性的相对重要程度，而且确定了后悔函数的形状，进而确定了后悔和欣喜的相对重要性.李梦等[11]针对RRM模型不能刻画出行者后悔程度的缺陷，通过引入后悔厌恶系数提出了基于后悔理论(Regret Theory,RT)的SUE模型.李梦甜等[12]将无差异曲线的概念内化到RRM模型中，构建了基于时间剩余的RRM模型.

此外，大量研究表明损失厌恶是人们重要的决策特征，并被相继内化到累积前景理论[13]、参考依赖理论[14]等行为选择模型中.然而，经典的RRM模型忽略了决策者的损失厌恶特性，且获益和损失产生的情绪差异仅是由偏好参数产生的附带效应所引起，并不能刻画决策者的损失厌恶程度[10].

基于以上考虑，本文在经典的RRM模型的基础上内化了出行者的损失厌恶特性，进而提出了一个改进的RRM模型.在改进的RRM模型中，等量的获益和损失所引起的欣喜和后悔程度的差异不仅源于偏好参数的尺度特征，而且也受到出行者损失厌恶的影响.

1 模型的建立

考虑1个道路交通网络G(N,A)，N是网络节点的集合，A是网络中所有路段的集合.假设该网络中共有W个OD对，Rw表示OD对w∈W的路径集；ta、Ca分别表示网络中路段a的走行时间和容量；xa表示路段a的交通流量；t0a表示路段a的自由流时间.类似地，Trw表示路径r∈Rw的走行时间成本；frw为路径流量，向量f=(frw,r∈Rw,w∈W)T为路径流量向量.网络中每个OD对w的交通需求固定为dw.

网络中路段、路径流量关系可表示为

路段的走行时间用BPR(The Bureau of Public Roads,BPR)函数表示为

1.1 经典RRM模型

经典RRM模型的核心是属性水平的后悔函数，用来表征考虑备选方案的后悔，即

假定出行者的感知后悔Hˉrw由系统项和随机项组成，那么感知后悔可表示为

假设随机误差项是独立同分布的Gumbel变量，根据RUM原则，均衡时出行者路径选择概率及网络流量模式为

式中：θ为一个离散参数，反映出行者的感知误差程度.

1.2 改进的RRM模型

为了能够在后悔理论的基础上内化出行者的损失厌恶特性，本文提出了MRRM(Modified Random Regret Minimization Model,MRRM)模型.在MRRM模型中，出行者在考虑备选和选择集中其他备选进行比较时，被认为可以分别感知属性的获益和损失.

1.2.1 基于损失厌恶的效用函数

为了体现出行者对获益和损失的偏好不对称性，我们首先提出了考虑损失厌恶的属性水平的后悔函数.假设u(r,d)为一个基于情景的二元效用函数，r和d分别为出行者的考虑备选和选择集中任一其他备选.

假设1u(r,d)=u(r-d).

假设1表明出行者在决策过程中会将考虑备选与竞争备选进行比较，同时也暗示该效用函数的结果仅依赖于考虑备选与竞争备选的差异.

假设2u(r-d)=u(Trw-Tdw).

假设2表明出行者在比较考虑备选与竞争备选时，将分别感知到考虑备选路径走行时间的获益和损失.

假设 3，η表示时间成本的系数，φ(φ≥1)表示时间成本的损失厌恶系数.

假设3用来描述出行者对潜在获益和损失的不对称偏好，并且暗示出行者对损失比等量的获益更加敏感.

1.2.2 考虑损失厌恶的RRM模型

为在RRM模型中体现出行者损失厌恶的影响，下面将带有损失厌恶的效用函数内化到RRM模型中，改进的RRM模型的后悔函数可表示为

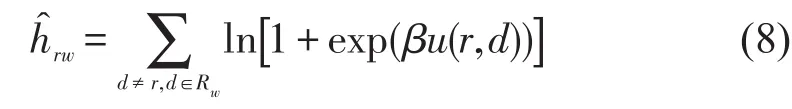
特别地，当η=φ且为1时，MRRM模型退化为经典RRM模型.在改进的RRM模型框架下，假定出行者的感知后悔为，那么有

假定随机误差项是独立同分布的Gumbel变量，则基于Logit的路径选择概率和网络流量模式为

1.2.3 后悔函数的比较

图1描述了2个后悔函数随属性差的变化情况.为便于分析，两个后悔函数中偏好系数β均被设为1，走行时间的系数和损失厌恶系数分别定为1.0和1.8.这样，讨论就可以被限定在后悔域，进而探究2个后悔函数所引起的后悔的差异.图1中水平虚线表示属性差为零时函数的后悔值，它和后悔函数曲线共同划分出后悔和欣喜2个区域.在RRM模型中，等尺度的获益和损失所引起的欣喜和后悔程度的差异，主要源于偏好参数的附带效应.然而，MRRM模型认为出行者的后悔由两部分组成：①出行者的偏好系数产生的后悔h1，②出行者损失厌恶产生的后悔h2.

图1 属性水平后悔函数Fig.1 The attribute level regret function

为分析偏好参数对MRRM模型的影响，图2刻画了不同尺度偏好参数下后悔函数的形状.由图2可知，不同偏好参数影响下后悔函数的形状完全不同.随着偏好参数的逐渐减小，表示属性为零的水平虚线不断上移，使等尺度的获益和损失产生的欣喜和后悔的差异逐渐变小.由图2(a)可知，当偏好参数较大时，水平虚线与水平轴非常接近，说明由损失产生的后悔是影响决策的重要因素.在RRM模型中，当偏好参数为1个较小的数时，等尺度获益和损失引起的欣喜和后悔的差异的显著性将消失，详细描述请见文献[15].也就是说，差异的产生源于偏好系数，而不是出行者的损失厌恶.而在MRRM模型中，如图2(d)所示，当偏好参数为1个较小的数时，由于出行者的损失厌恶这样的差异仍然存在.因此，在MRRM模型中，偏好参数反映的是后悔函数的形状，即后悔和欣喜的相对重要程度.这样，由等尺度获益和损失所引起的欣喜和后悔的差异受到偏好参数和出行者损失厌恶的共同影响.

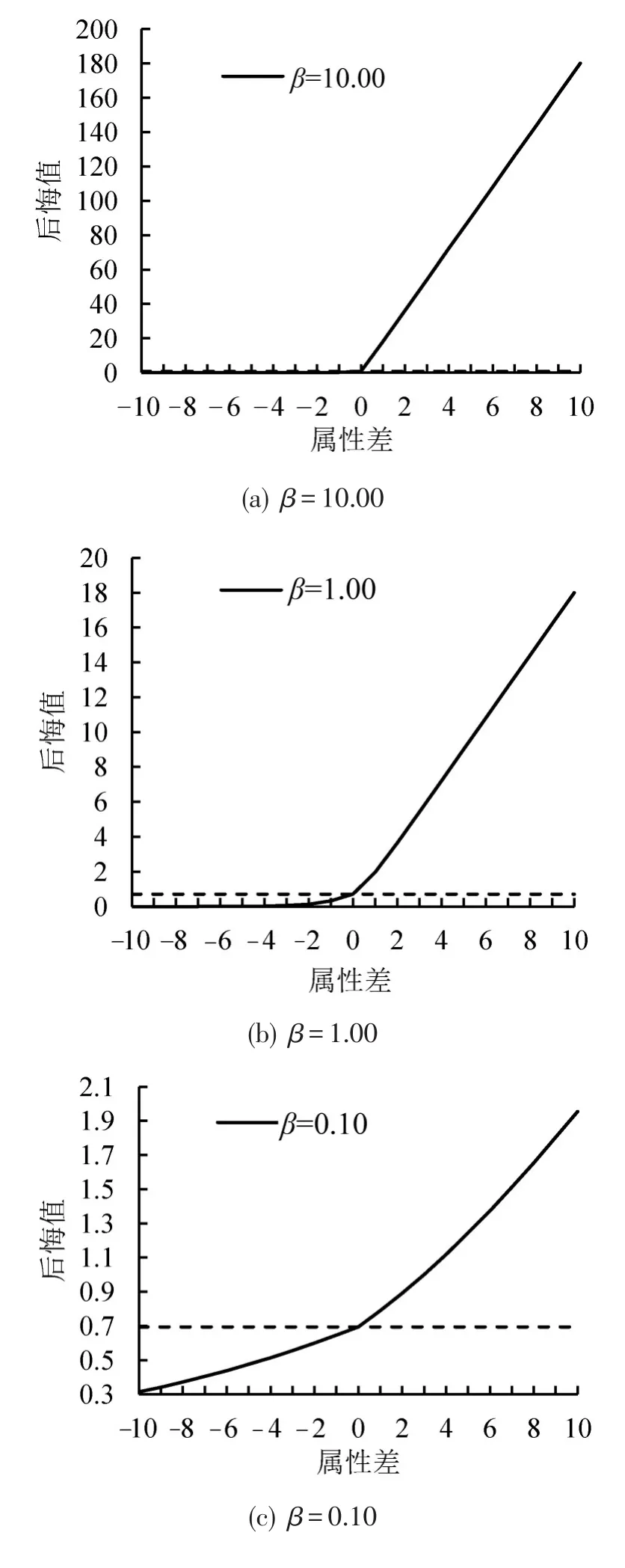
图2 不同尺度偏好参数下改进后悔函数的形状Fig.2 The shapes of improved regret function for the taste parameter with different sizes

1.3 等价的变分不等式问题

MRRM模型可以表示为变分不等式问题，即

式中：Ω是1个闭凸集，表示路径流量的可行域，即

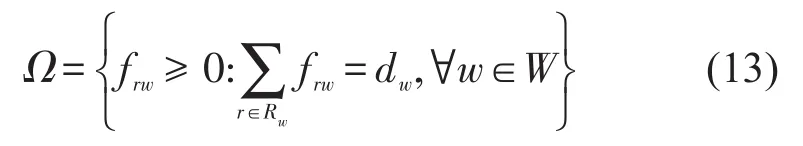
定理1MRRM模型的均衡条件式(10)和式(11)与变分不等式问题式(12)是等价的.

证明由变分不等式问题式(12)的KKT条件得

式中：μw为式(2)的拉格朗日系数.

变换式(14)为

结合式(2)和式(15)，可得

再将式(16)代入到式(14)中，均衡条件式(10)和式(11)可以被推出.因此，该变分不等式问题等价于基于Logit的网络均衡条件式(10)和式(11).

定理2等价的变分不等式问题式(12)至少有1个解.

证明由于该变分问题的可行域是1个非空的、紧致的凸集，函数是关于frw连续，根据Brouwer不动点定理，该变分不等式问题至少存在1个解.但是，一般而言，prw的严格单调性不能保证，因此该变分不等式问题式(12)的解的唯一性不能确定.

2 求解算法

本文采用相继平均法(Method of Successive Average,MSA)对模型进行求解.算法的具体步骤如下：

Step 1初始化.置迭代次数n=0，迭代终止误差ε=0.001.基于给定的OD交通需求，产生初始可行流量向量f(0).

Step 2计算.根据路径的走行时间Trw，首先根据假设1～3计算考虑损失厌恶的效用函数，而后将结果代入后悔函数式(8)计算各考虑路径的后悔值.

Step 3流量更新.设y为流量向量f的辅助流量向量，辅助流量由式(11)确定.用MSA算法更新路径流量为

Step 4收敛性判断.若ε，则输出的解即是最优解，计算结束；否则，令n=n+1，返回Step 2.

3 数值算例

考虑如图3所示的路网，该路网由1个OD对、6个节点、5条路径和8个路段组成.定义网络总的交通需求为4 000，路段的自由流时间t0a和通行能力Ca如表1所示.

图3 算例网络Fig.3 The example network

表1 路段的自由流时间和通行能力Table 1 Link free-flow time and capacity

在数值案例中，本文假设离散参数θ为1，偏好系数为0.5，走行时间系数和损失厌恶系数分别为0.2和2.5.表2给出了不同随机用户均衡条件下的网络均衡流量模型.

表2 不同SUE模型的流量模式Table 2 The equilibrium flow pattern of different SUE models

由表2可知，不同的SUE模型给出了不同的均衡流量模式.由RUM-SUE模型的均衡结果，可以发现OD对1→3的大部分出行者选择了路径2，OD对2→4的大多数出行者选择了路径3，而在2个后悔随机用户均衡模型中，2个OD对的出行者选择OD对相关路径的比例比较接近，路径流量分布更加均衡.均衡结果的不同主要源于决策机制的差异，RUM-SUE模型假定出行者倾向于选择感知走行时间最短的路径，而RRM-SUE和MRRMSUE模型认为出行者总是更倾向于选择预期后悔最小的路径，其路径选择行为与考虑路径和备选路径的属性差有关，是一种基于情景的行为选择机制.

图4描述了偏好系数变化对出行者路径选择行为的影响.其中走行时间系数和损失厌恶系数分别为0.2和1.0，离散系数θ保持不变.如图4所示，随着偏好系数的增大，两个OD对的出行者更倾向于选择最短路径(如路径2和路径4).由于较小的偏好系数暗示出行者对后悔和欣喜的重视程度差异较小，这样就导致同一OD对的出行者选择2条路径的概率相差不大；此外，随着偏好系数的逐渐增大，出行者越来越重视后悔，使得非最优路径的选择概率逐渐减少(如路径1和路径3)，最优路径的选择概率逐渐增大，最优路径和非最优路径选择概率的差异不断扩大.

图4 偏好系数对出行者路径选择行为的影响Fig.4 The effects of taste parameter on travelers’route choice behavior

离散参数θ也是影响出行者路径选择行为的重要因素.图5通过以OD对1→3的路径1为研究对象，刻画了不同决策机制下离散系数对出行者路径选择行为的影响.由图5可知，2个SUE模型所确定的路径1的选择概率均随着离散系数的增大而减小.并且，可以发现RUM-SUE模型对离散参数的变化更敏感.

图5 离散参数对出行者路径选择行为的影响Fig.5 The effects of discrete parameter on travelers’route choice behavior

图6进一步给出了损失厌恶对出行者路径选择行为的影响.其中，走行时间系数设为0.2，离散参数θ仍为1.0.由图6可知，随着偏好系数的增大，路径1的选择概率逐渐减少；同时，在相同偏好系数情况下，随着出行者损失厌恶的增大，出行者选择路径1的概率降低.这样的选择行为变化的原因可解释为：由于1个大的损失厌恶系数暗示出行者对走行时间的损失更加敏感，而路径1非OD对1→3的最优路径，因此当出行者选择路径1时，将产生更大的后悔，进而使路径1的选择概率变小.由此可证明，出行者的损失厌恶对其路径选择行为有较大的影响.

图6 损失厌恶对出行者路径选择行为的影响φFig.6 The effects of loss aversion on travelers’route choice behavior

4 结论

本文在经典随机后悔最小化模型的基础上，通过引入出行者损失厌恶的决策特征，提出了改进的随机后悔最小化模型，进而分析了出行者损失厌恶对其路径选择行为的影响.特别地，改进的随机后悔最小化模型可以退化为经典的随机后悔最小化模型.因此，改进的随机后悔最小化模型对于出行者路径选择行为模拟显得更加灵活.为验证本文所提出的改进的随机最小化模型，一个算例网络被设计对其进行验证分析.研究结果表明，出行者对后悔和欣喜的重视程度及损失厌恶的水平确实会对其选择行为产生比较大的影响，同时也暗示科学、合理的交通管理政策的制定要充分考虑出行者的决策特征.此外，本文并未考虑出行者偏好的异质性和动态的学习过程，改进的随机后悔最小化模型仍有待进一步研究.