Iterated Hardy-Littlewood maximal function*
WANG Zequn, YAN Dunyan
(School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China) (Received 28 March 2017; Revised 26 April 2017)
Abstract In the paper, we investigate the iterated non-centered Hardy-Littlewood maximal function and the iterated centered Hardy-Littlewood maximal function. We prove that the limit of the iterated maximal function is just a fixed point of maximal operator. As an application of the fixed point theory, we finally obtain that the fixed point is ‖f‖∞ for non-centered Hardy-Littlewood maximal operator. The same is true for the centered Hardy-Littlewood maximal operator only for n=1,2.
Keywords Hardy-Littlewood maximal function; fixed point; iterated Hardy-Littlewood maximal function
Define the centered Hardy-Littlewood maximal function by
(1)
and the non-centered Hardy-Littlewood maximal function by
(2)
whereBis a ball andB(x,r) is a ball with the center at the pointxand the radiusr. The basic real-variable construct was introduced forn=1 by Hardy and Littlewood[1]and forn≥2 by Wiener[2]. It is well-known that the Hardy-Littlewood maximal function plays an important role in many parts of analysis. It is a classical mean operator frequently used to majorize other important operators in harmonic analysis.
It is clear that
Mcf(x)≤Mf(x)≤2nMcf(x)
(3)
holds for allx∈n. BothMandMcare sublinear operators and the two functionsMfandMcfnever vanish unlessf=0 almost everywhere[3]. The study of the boundedness forMorMcis fairly complete[4]. The primary purpose of this paper is to study the properties of the iterated Hardy-Littlewood maximal function.
LetMbe the non-centered Hardy-Littlewood maximal function defined by (2). Define the iterated non-centered Hardy-Littlewood maximal function denoted byMk+1as follows:
Mk+1f(x):=M(Mkf)(x),
(4)
fork=1,2,…, andx∈n. SetM1f(x):=Mf(x).
In the same way, we can set
(5)
We all know that both operatorsMcandMhave theLp-boundedness and the two maximal functionsMcfandMfhave a little difference in the pointwise sense from inequalities (3). We want to investigate the limit of the iterated Hardy-Littlewood maximal function.
Wei et al[5]studied the limit ofMkfand obtained Theorem A as follows.
TheoremAFor anyf∈L∞(n), the equation
(6)
holds for anyx∈n.

Now we formulate our main results as follows.
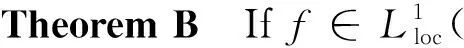
(7)
holds for everyx∈nif and only ifn=1,2.
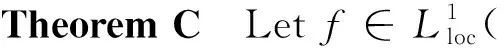
for everyx∈nand anyn∈N.
We remark that the range of functionfin Theorem C is wider than that in Theorem A. Furthermore in this paper we will use some novel ideas to prove Theorem C.
1 Fixed point of Hardy-Littlewood maximal operator
To prove our main theorems, we first provide some definitions and lemmas which will be used in the follows. Some lemmas can be found in classic literatures and here we omit their proofs.
Definition1.1A functionFis called a fixed point of a operatorT, if
TF(x)=F(x)
(8)
holds for allx∈n.
Obviously ifFis a fixed point of the operatorT, then we have
By the Lesbegue differentiation theorem, for almost allx∈n, we have
Mcf(x)≥|f(x)|
and
Mf(x)≥|f(x)|.
For the iterated Hardy-Littlewood maximal operator, we have the following lemma.
Lemma1.1Forx∈n, andk≥1, the two inequalities
Mk+1f(x)≥Mkf(x)
(9)
and
(10)

ProofSetE={x:xis not the Lesbegue point of |f|}. It follows from the Lesbegue differentiation theorem thatm(E)=0. Actually we merely need to prove
M2f(x)≥Mf(x)
for allx∈n.
We conclude that
=M2f(x).
(11)

□
By Lemma 1.1, sinceMkfmonotonously increases, the limit ofMkf(x) exists for allx∈n.
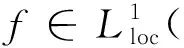

Fort>0, set
ft=f*φt,
whereφt(x)=t-nφ(x/t), for allx∈n. Obviously we have
ft∈C∞(n).
Put
The centered Hardy-Littlewood maximal function is written by
(12)
Notefis a fixed point ofMc. This impliesf≥0. We have that
=ft(x).
(13)

Mc(ft)(x)≥ft(x).
Thus we obtain thatftis a fixed point ofMc.
Using the similar method, we can easily prove thatftis a fixed point ofMiffis a fixed point ofM.
□


Lemma 1.3 is due to that for a smooth function, every point innis its Lesbegue point. We only need thatf(x)≥Mf(x) to guarantee that the function is a fixed point.
Lemma1.4Iffis a non-constant and smooth function, andfis a fixed point ofM, then, in any closed ball, the minimum value offis gotten only in the sphere.
Lemma 1.4 has the same proof as the proof of extremism principle of harmonic function. For the details please see Ref.[6].
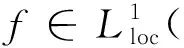
Proof. Sincefis a fixed point ofM, it follows from Lemma 1.2 that there existsft∈∞(n) such thatftis a fixed point ofMas well.
Suppose thatBis a ball innandft∈∞(n)n) such thatMft(x)=ft(x) for allx∈n. We use the proof by contradiction.
Ifftis not a constant, then, by Lemma 1.4, there is at least one pointx∈∂Bsuch thatft(y)>ft(x) holds for ally∈B°.
Note thatftis a fixed point ofM. Thus we have that

(14)
This is impossible. Consequently it implies thatft(x)=Cfor allx∈n.
Next we will prove thatf(x)=Cfor allx∈n.

⊂{x∈n:|x|≤1}
andφ(x)≥φ(x′) for 0≤|x|≤|x′|.
For eacht>0, we haveft(x)=C.
SetBR={x∈n:|x|
=fχBR*φt(x)+fχ*φt(x).
(15)
It follows from (15) that
(16)
(17)
for almost everyx∈n. By the property of convolution, we get that
suppfχ*φt⊂{x∈n:|x|≥R-t}.
(18)
Combing (16), (17) with (18) yields that
holds for almost everyx∈n. This is equivalent to that
fχBR(x)=C
holds for almost everyx∈n. LetR→∞, then we have
f(x)=C
for almost everyx∈n. This implies thatMf(x)=Cfor everyx∈n. Note thatfis a fixed point ofM, that is,
Mf(x)=f(x).
Thus we must obtain that
f(x)=C
for everyx∈n.

We haveMf(x)=∞. So we havef(x)=∞ for everyx∈n.
□
We remark thatMchas essential difference withMwith respect to the fixed point. We all know that whenn≥3, the functionf(x)=|x|2-nis a harmonic function inn{0}. In fact, we can easily check thatf(x)=|x|2-nis a fixed point ofMc.
Korry[7]obtained the following lemma 1.6.
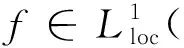
2 Main theorems
In the section, for any local integral function, the limit of the iterated Hardy-Littlewood maximal function is a fixed point of Hardy-Littlewood maximal operator.
Theorem2.1Write
We have
MF(x)=F(x).
That is,Fa fixed point ofM.
In the same way, write
thenMcFc(x)=Fc(x). That is,Fca fixed point ofMc.
ProofWe only prove the first part of Theorem 2.1. It follows that

(19)
Associate to an arbitraryε>0Bεxsuch that
≤MF(x).
(20)
That is
MF(x)=F(x).
(21)
□
Lemma2.1Write
IfF(x)=Cfor allx∈n, then we haveC=‖f‖∞.
ProofSinceF(x)=C, it implies from the definition of Hardy-Littlewood maximal function thatC≤‖f‖∞. By the definition of essential supremum of function, associate to an arbitraryε>0, a setE⊂nwithm(E)>0, such that
|f(x)|>‖f‖∞-ε,
forx∈E. Whenx∈Eis the lebesgue point off, we have that
C=F(x)≥Mf(x)≥|f(x)|>‖f‖∞-ε.
By the arbitrary property of ε, we immediately have
C≥‖f‖∞.
Consequently we haveC=‖f‖∞
□
Next we will prove our main theorems.
TheproofofTheoremB
ProofIt follows from Theorem 2.1 that
(22)
is a fixed point ofMc.
SinceFc(x)=C, it implies from the definition of center Hardy-Littlewood maximal function thatC≤‖f‖∞.
By the definition of essential supremum of function, associate to an arbitraryε>0 a setE⊂nwithm(E)>0, such that
|f(x)|>‖f‖∞-ε,
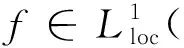
C=F(x)≥Mcf(x)≥|f(x)|>‖f‖∞-ε.
By the arbitrary property of ε, we immediately have
C≥‖f‖∞.
Consequently we haveFc=‖f‖∞.

□
TheproofofTheoremC
ProofIt follows from Theorem 2.1 that
(23)
is a fixed point ofM.
It follows from Lemma 2.1 thatF=‖f‖∞.

Note thatFa fixed point ofM. We have
F(x)=MF(x)=∞.
Consequently, we haveF=‖f‖∞.
□

