基于时频分析法研究黄河河道坝垛根石厚度
张宏杰 郭乙霏 李广超 侯超普 陈萌


摘要:黄河中下游河道整治工程坝垛水下的散抛石块体大小不一,散乱堆砌成有坡度的堆石薄层,采用非接触式探All方法探测时绕射波比较强烈。根石探测数据主要在时间域处理,仅能人工拾取得到根石顶界面,很难识别根石底界面,无法在时间域获取根石厚度。通过对叠后时间偏移的探测数据作频谱分析与s变换,获取河床泥沙段与根石段的频谱特征;根据河床泥沙与根石段的时频特征差异,设计识别根石的算法;利用时频分布图中频率在时间维度的延续计算根石的厚度,实现自动化识别,避免了人工识别波形造成的误差。
关键词:河道整治工程;根石;声波;时频分析;频谱响应;黄河
中图分类号:TV871.2;TV882.1 文献标志码:A
黄河中下游河道整治工程以坝垛调控河流走势,受河水冲刷影响,经常发生根石走失现象。探测清楚根石的缺失状况,在汛后的加固处理中就会有针对性,避免治理工作的盲目性。非接触式根石探测方法主要是采用浅地层剖面仪获取根石的声波反射资料,并加以分析处理。泥沙、根石、河水之间存在较大的波阻抗差异,存在明显的反射界面,在资料处理过程中,人工能够较清晰地识别根石顶界面,但根石厚度较小,堆砌有一定的坡度,且块石大小不均匀、堆砌散乱,在浅地层剖面仪获取的记录上形成较强的绕射,根石界面的反射波和绕射波及各种干扰波混叠在一起,没有办法在时间域获取根石厚度和坝前的最大冲刷深度。通过对叠后时间偏移的浅地层剖面数据作频谱分析与S变换,可获取河床泥沙与根石段的频谱特征。笔者根据河床泥沙与根石段的时频特征差异,设计识别根石的算法;利用时频分布图中频率在时间维度的延续计算根石的厚度,以实现自动化识别。
1 频率敏感性统计
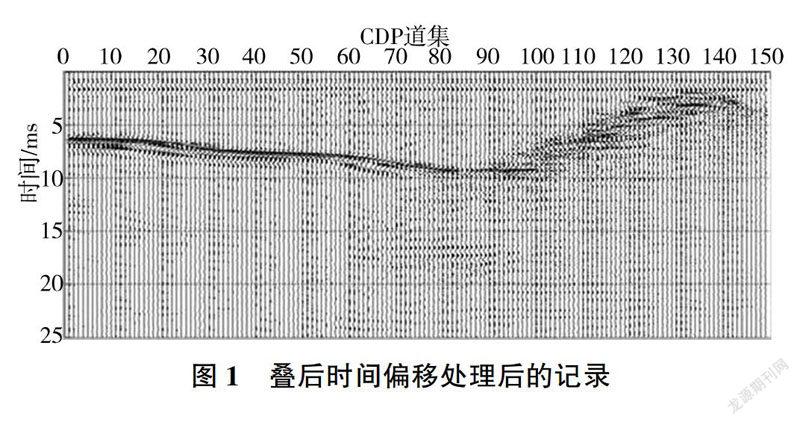
原始记录经过叠后偏移处理后可以看出,1~80道的记录为泥沙段反射波,平滑连续,能量集中,并且在泥沙界面之下没有其他反射波的存在,只有一些多次波的存在;81~150道记录为根石段反射波,有较强的绕射波,有一定的延续度,见图1。
从时间记录很难识别出根石的厚度,需要将声波道集进行时频分析,并将时频分析后的数据按照频率进行振幅统计,并做归一化处理。图2为所有150道数据的时频分析频率統计,可以看出统计图上有两个峰值,其中的低频段在1300Hz附近,整体能量较强,均高于高频段的峰值;高频段的峰值在4000Hz附近,整体能量分布不太集中。
根据波形图中反映的根石和泥沙界面段,拾取相对应的两个时间窗口,将这两个时窗段内的频率谱分别进行统计。图3为泥沙段的频率统计,可以看出和图2之间有着很明显的差异。图3中低频能量过强,为了便于比较做了限幅,在高频段有非常微弱的峰值迹象。图4为根石段的频率统计,有两个比较明显的峰值,两个峰值对应频率分别为1300Hz和4500Hz。这和图2是一致的,因此可以从频率域来分析泥沙和根石的界面,根据高频成分的延续来获取根石的厚度。2频率域分析处理
信号的有效信息不仅可以在原始时间域中提取,也可以转换到其他合适的域中提取。当前能从3个方面获取蕴含在信号中的信息:时间域、频率域、时频分布。根石厚度的问题类似于一定倾角的超薄地层问题,考虑河水、泥沙、石块的反射吸收系数不同,获取的信号资料有不同的频率响应,将它们对应的频率响应展现在时间维度上,获得其顶、底界面的纵向延伸,就可以划分出它们之间的界面。可以说,信号频率在时间上的分布显得至关重要,区分根石的顶、底界面的反射波信号,获取根石对应频率分布的时间区间,就可以计算出根石的厚度。
傅里叶变换是信号处理中最常用的方法,该变换是在时间域和频率域的整个空间展现信号的,是全局的整体变换,可得到信号的频率分布情况,但其时间分辨率为零[1]。还有常用的Hilbert变换方法Teager -Kaiser方法、Shekel方法,属于非时频方法的瞬时频率估计[2],得到的是单值函数,能处理任何时刻单一频率的信号。浅地层剖面仪发射频带范围为0.5~7.0kHz,经过水下介质滤波作用后被探头接收的信号包含多种频率成分,用这些非时频方法得到的瞬时频率和实际信号的自身频率完全不能对应,也就失去了其大部分的应用价值。
时频分析技术能够表征信号的频率随时间的变化,其核心思想是构建一个时间和频率的密度函数,将每一道的一维时间信号映射到二维的时间一频率平面,展示信号频率是如何随时间变化的,不仅解决了傅里叶变换没有时间分辨率的问题,也克服了Hilbert变换等方法只能处理单一频率的不足。利用时频分析结果能够做出时频分布图形(二维或三维),指示每一时刻的信号在瞬时频率附近的能量聚集情况,等效的时域信号可以通过时频表示的求逆过程得到[3]。赵淑红等[4]利用短时傅里叶变换的时频分析研究沉积旋回,取得了很好的效果。
时频分析的线性时频表示主要有短时傅里叶变换、小波变换、S变换等,二次型时频表示反映信号能量分布的有Wigner-Ville分布等。
短时傅里叶变换基本思想是将信号加滑动时间窗,也就是傅里叶变换乘上一个有限时间单元的窗函数,对时间窗内信号作傅里叶变换,将窗函数沿时间轴按照一定的步距移动,从而实现信号的逐段分析,得到信号的时变频谱。短时傅里叶变换是目前研究非平稳信号有力的工具,在各个领域中应用广泛。
短时傅里叶变换(STET)定义为[5]式中:f为频率;t为时间;h(τ)为信号;w(τ-t)为窗函数。
根据Heisenberg测不准原理[6],一旦窗函数选定,时频分辨率便确定下来,在窗口形状不变的情况下,窗口面积越小,时频表征局部化的能力就越强。要提高时间分辨率,就要选择的窗函数尽可能短;要提高频率分辨率,则要求窗函数的时间宽度尽可能长。短时傅里叶变换虽然能描述时频的变化情况,但它在时域、频域的分辨率Δt、Δf不随时间t和频率f的变化而变化,不能敏感地反映信号的突变,适用于对缓变信号的分析,对突变信号和非平稳信号的分析存在局限性。对于采集的时间序列信号,很难找到一个合适的时间窗函数来适应不同的时段[7]。
S变换是介于短时傅里叶变换(STFT)和小波变换(WT)之间的一种非平稳信号分析和处理的方法,综合了短时傅里叶变换和小波变换的优点[8]。它的时间一频率谱分辨率与频率相关,不但有多尺度聚焦性,而且直接与Fourier谱联系,保持频率的绝对相位,基本变换函数不必满足容许性条件[9-13]。信号h(t)的S变换表示为[14]式中:w(t)为窗函数;σ为频率的函数。
3 时频分布特征
分析由浅地层剖面仪获取的资料,抽取其中包含河床泥沙段和根石段的150道记录进行分析,单道时间域采样点数1446,采样频率21739Hz,采样时间0.046ms(见图1)。利用几种时频分析方法,分别对每一道记录进行时频分析,获取单道数据的时频分布,对比总结出反射波在泥沙和根石界面的时频分布特征:河床泥沙段的时频分布特征是频率能量具有较小的时间延续度,并且能量较强,强度超过180;根石段的时频分布特征是在频率1000~6500Hz范围内有较大的时间延续度,能量比较分散,能量强度小于100。图5为河床泥沙段(CDP25、CDP45)和根石段(CDP100、CDP130)单道记录的S变换时频分布。
图6为S变换的时频分布,分析的时间点数为480。可以看出1~85道泥沙段的频谱具有明显的特征:能量强,连续圆滑,一致性好。86~140道的根石段频谱能量特点是能量比较强,能够看出根石的轮廓,有比较圆滑清晰的下边界,也就是根石的底部反射,利用这些信息可以确定根石的厚度。
4 根石厚度估算
根据泥沙段和根石段的时频分布特征,反射记录经过S变换,按照图1记录道集方式展示时频分布图,利用式(5)计算时频分布属性,并设定:任意点数据的反射能量强度超过120后,将其能量强度降低到20,其目的是突出根石反射的能量强度,便于利用时频分布图自动识别根石(见图7)。式中:A(i,j)为频率分布的能量强度;tf(i,j,k)为第i道记录第j个采样点、第K个频点的时频分布。
图7中较深色块表示根石反射范围,其边界是明显的,可以方便地估算水的深度和根石的厚度。剖面中任何位置的根石厚度和水的深度都可以根據图7中深颜色区域的频率分布区间对应的时间值估算。例如,在位置CDP120,考虑到传播时间声反射双程旅行时间,该处水深1.875m或双程时2.5ms,根石厚度5.5m或双程时5ms,根石中的平均传播速度设定为2200m/s。计算每一处的根石厚度都需要声波在该处根石中传播的速度,这个速度受到根石块大小、堆放情况、充填物情况的影响,没有办法获取精确的速度,需要采用平均速度,平均速度的获取需要一定的经验积累和验证。
5 结论
(1)信号的频率响应在泥沙反射段和根石段之间的能量分布有一定差别,泥沙段优势频率为1300Hz,根石段优势频率为4500Hz,根石段的优势频率主要是高频成分。
(2)河床泥沙段的时频分布能量比较集中,光滑连续,在时间维度的延续比较短;根石段的时频分布能量相对集中,上下界面清晰但不规则、不光滑,时频分布在时间维的延伸较大。
(3)S变换比较适用于倾斜薄层信号处理,获取了根石段信号在时间维度的延续,就能够求取散抛的薄层根石厚度。
参考文献:
[1]张贤达,保铮.非平稳信号分析与处理[M].北京:国防工业出版社,1998:35-48.
[2]李世雄,陈东方.信号瞬时参数计算方法评价[J].信号处理,2003,19(1):59-63.
[3]ROESSGEN M,BOASHASH B.Time-Frequency Peak Filte-ring Applied to FSK Signals[C]//Ieee-Sp International Sym-posium on Time-Frequency and Time-Scale Analysis.IEEE,1994:516-519.
[4]赵淑红,张文波.短时傅立叶变换在研究沉积旋回地质体中的应用[J].长安大学学报(地球科学版),2003,25(2):59-62.
[5]刘丽娟.时频分析技术及其应用[D].成都;成都理工大学,2008:20-25.
[6]何旭,李鸿光.利用经验模式分解提高短时傅立叶变换分辨率[J].广西师范大学学报(自然科学版),2005,23(1):5-8.
[7]葛哲学,陈仲生.Matlab时频分析技术及其应用[M].北京:人民邮电出版社,2006:36-40.
[8]周开明,刘贤红,查树贵,等.几种时频分析技术的性能研究及在河道砂体预测中的应用[J].天然气工业,2007(s1):451-453.
[9]COHEN L.Time-Frequency Analysis:Theory and Application[M].Englewood Cliffs,NJ;Prentice Hal,Inc,1995:20-25.
[10]GARBOR D.Theory of Communication[J].The Journal of theInstitute of Electrical Engineers,1946,93(3):429-456.
[11]刘喜武,年静波,黄文松.利用广义S变换提取地震旋回的方法[J].石油物探,2006,45(2):129-134.
[12]刘财,张海江.小波变换及其在薄储层识别中的应用[J].石油物探,1995,34(3):23-31.
[13]孙鲁平,郑晓东,首皓,等.薄层地震峰值频率与厚度关系研究[J].石油地球物理勘探,2010,45(2);254-259.
[14]蒋龙聪.薄互层储层地震响应时频分析研究[D].武汉:中国地质大学,2008:55-60.

