物流配送网络最短路线规划

刘婷婷 于卫红

摘要：物流配送网络最短路线的规划不仅能提高商品运输效率，还能节约时间成本和运输成本。本文根据物流配送最短路线规划的现状，利用最小生成树法对现有问题进行分析。通过资料整合、建立实例模型、使用Kruskal算法建立模型、比较权值大小并用canvas画布显示最终路径图形等过程，得出物流配送网络的最佳路径，最后用Java实现整个模型，得出最短路径和最低时耗方案。

关键词：最小生成树;Kruskal算法;物流配送中心;最短路径规划

引言

电子商务作为一类崭新的商业模式，与传统商业模式下配送中心不同的是，電子商务时代下的配送中心往往需要提供送货上门的服务，这也成为了一笔额外的支出，因此，规划出合理的路线图也是很重要的。目前关于物流配送网络问题，研究方法主要有运筹学的应用、仿真技术评价方法、遗传算法等。研究也主要集中于解决时间最优和配送中心最优选址的问题，研究成果主要有：2013年，赵慧娟、汤兵勇、张云在《基于动态规划法的物流配送路径的随机选择》提出在基本的动态规划算法基础上，结合物流配送的路径选择问题，引入配送途中道路的拥堵因子，随机修正配送路径的相应权值，动态调整选择配送路径。2015年，朱金凤在《基于成本约束的冷链物流配送网络规划》中提出了“服务半径”的概念，将物流节点的配送时耗转换为物流节点的服务半径，并最终通过一系列的约束条件来表示决策变量之间的关系。2015年，钮亮、张宝友在《基于云计算求解城市物流配送最短路径研究》中提出了基于MapReduce的并行算法和GIS仿真结合的求解方法。虽然目前解决物流配送最短路径规划的方法有很多，但是也存在着一些不足之处。本文基于目前的研究成果，采用Kruskal算法构建物流配送网络最短路线规划模型，并用实例进行了验证。

1、物流配送最短路线规划相关算法简介

目前关于最短路线的主要研究方法有整数线性规划法、Dijkstro算法、Floyd- Warsholl算法、遗传算法、Bellman-Ford算法、蚁群算法等。

Dijkstro算法利用起点为中心，向外层层扩展，最终求解出最短路径。但是，Dijkstra算法只适用于权值非负的情况，当权值为非负的时候，就不再适用了。Floyd-Warshall算法解决了弧长必须非负的问题，但是面对只需从一个顶点到其他各个顶点最短距离的问题时，Floyd-Worshall算法的时耗非常长。遗传算法，原理来自于生物界优胜劣汰的进化规律，是一种随机化搜索的方法。首先通过对问题的参数集进行编码，随机产生一个种群，计算适应函数和选择率，进行选择、交叉、变异操作，直到满足迭代收敛条件为止。受启发于蚂蚁在寻找食物过程中的路径的行为的蚁群算法，具有分布计算、信息正反馈和启发式搜索的特征，本质上是进化算法中的一种启发式全局优化算法。

此外，近年来还提出了一些新的算法，比如，基于最短路径的局部随机游走方法、求解点到点的最短路径的高效下界算法以及在路网上检索k近邻的基于预处理的近似算法等。

Kruskol算法相对于以上算法简便、易于实现，对解决结点比较少的情况，执行效率高。因此，本文用Kruskal算法构建模型研究了大连海事大学邮件收发中心快递配送的最短路径规划问题。

2、基于Kruskal算法的最短路线规划模型

Kruskol算法的主要思想是从源结点开始，按路径长度递增的次序，依次找结点到源结点的最短通路，从而产生最短路径。

使用该算法对物流配送网络最短路线进行规划主要遵循如下步骤：

（1）初始化顶点：给所有顶点编号，并将顶点序号存储在顶点数组之中。将图的信息按照起点、终点、权重的顺序存储在结构体数组edge中（如公式1所示）。

edge.start= start; edge.end= end;

edge.weight= weight

（公式1）

（2）权重排序：将所有权重按照从小到大的顺序排序，并设置临时变量存储最小权重，式中edge[edge size（）] .weight表示带权路径图的所有权值（如公式2所示）。

Minweight=min{edge[edge.size（）] .weight（公式2）

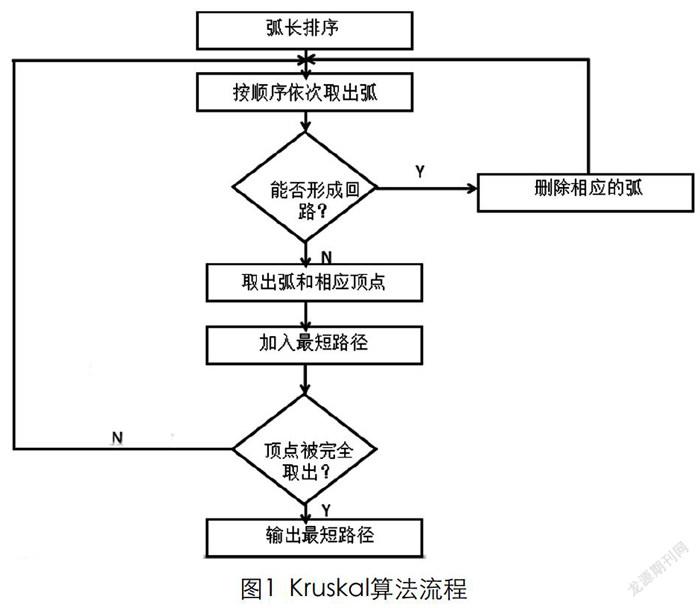
（3）构建最小生成树：按照权重从小到大的顺序依次将弧和相应的顶点取出，在每次取的时候判断是否会形成回路，若形成回路，则删除弧，依次构建最小生成树（如图1所示）。

3、实例：大连海事大学邮件收发中心快递配送最短路径规划

3.1 建立校园矢量图

本实例选取了大连海事大学邮件量最多的8个教学楼与实验楼为例，首先通过百度地图建立校园矢量图，图中各个配送点的位置是基于实际位置和实际大小的关系而建立的，以确保后期利用该矢量图求最短路径的准确性，建立校园矢量图（如图2所示）。

3.2 数据测量

以邮件中心和各个配送点为节点，根据实际情况，一共有36条配送路线，为确保实际距离和路线的准确性，经过多次人工测量、百度地图检验，得到各节点之间的距离长度（如图3所示）。

3.3 数据导入及处理

将实际距离的数据作为各节点之间的权重，导入到Java程序中，并存放在data文件中，从文件中将数据导入到Java程序中。为了简化数据，将邮件中心、知行楼、机电楼、图书馆、积学楼、水上训练馆、综合楼、文海楼、管理楼，依次用数字1-9表示（如图4所示）。

在Java程序中用sort函数对导入的实际距离数据进行排序，得到的排序结果（如图5所示）。

3.4 Kruskal算法对最短路径的实现

实际距离排序之后，运行程序，得到路线模型图以及最短路径结果图（如图6所示）、（如图7所示）。

研究中使用Javo语言对上述算法进行了完整的实现，程序执行后，生成如图6和图7的路线模型，在画布中实现最小生成树，并得出最终最小生成树的路径总长度为3978米，最短路线为2->3、3->5、4->5、8->9、7->9、5->6、1-->4、5->8，即表示从邮件中心到各个配送点的最终路线（如图8所示）。

4、结论

在原有配送网络的基础上，对配送路线进行合理地规划，不仅能够及时地满足客户的需求，而且可以节约配送中心的运输成本。本文结合实例，选择Kruskal算法作为生成最短路径的算法，并利用Javo实现，得到物流配送网络的最短路径。

在实际工作中，配送路线会受到很多外在因素的影响和制约，后续研究中，将综合考虑地理环境、交通状况等因素对配送的影响，使得最终的物流配送最短路径更加符合实际需求。

参考文献：

[1]赵慧娟，汤兵勇，张云.基于动态规划法的物流配送路径的随机选择[J].计算机应用与软件，2013，30（04）：110-112.

[2]朱金凤，苌道方，林丹萍.基于成本约束的冷链物流配送网络规划[J].江苏农业科学，2015，43（11）：572-575.

[3]钮亮，张宝友.基于云计算求解城市物流配送最短路径研究[J].科技通报，2015，31（05）：184-188+213.

[4]曹鲁寅，罗斌，钦明浩.用遗传算法求解最短路径问题[J].合肥工业大学学报（自然科学版），1996（03）：112 -116.

[5]沈显君著，自适应粒子群优化算法及其应用：清华大学出版社，2015.06

[6]王云峰.基于最短路径的随机游走算法研究与应用[D].北京交通大学，2012.