燃烧室出口温度场多维度分析的方法研究

邹俊 徐艳冰 王启道 王利 宋阁

摘要：为深入挖掘燃烧室出口温度场试验数据中所隐含的内在信息，基于数理统计理论和燃烧室出口温度场的分布特性，总结归纳了大量温度场数据的分析方法。并通过联机分析处理（On-Line Transaction Processing，OLAP）技术的思路形成涵盖整体、局部、微观、动态4个维度的温度场数据分析体系。并以某燃烧室的出口温度场数据为例阐述了该分析方法的内涵，使该温度场数据被多角度、多侧面、多层次的考察分析，验证了该分析方法的有效性。最后对多维度分析方法在温度场特性研究、无量纲化的比较、差异的量化分析等方面的应用进行了初步探索。

关键词：燃气涡轮发动机;燃烧室，出口温度场;多维度;分析方法

中图分类号：V235A2+3 文献标识码：A

燃烧室是航空发动机的重要部件之一。燃烧室的出口温度分布品质，特别是热点温度，对涡轮性能和热端部件寿命有直接的影响[1～3]，是涡轮等热端部件运行过程中必须考虑的问题。不同国家对衡量出口温度场分布品质的技术指标有不同的要求，国内一般用周向温度分布系数（Circumferential Temperature Distribution Factor，OTDF）和径向温度分布系数（Radial Temperature Distribution Factor，RTDF）等来评定温度场品质[4]。国内学者在温度场的深入分析等方面也进行了很多探索研究，如刘富强等提出了用局部扇形区域径向温度沿叶高的分布特性这一概念来考核燃烧室出口温度品质[5]，王兵等对多组温度场数据进行对比分析，建立了径向、周向分布曲线以及可视化图形等[6]，张树林等引入模糊原理，介绍了一种温度场数据的统计方法[7]。在国外，俄罗斯对出口温度场的分析，除了国内所要求的指标外，还包括质量系数及曲线斜度等[6]。

因此，本文从多维的角度，开展燃烧室出口温度场数据的分析方法研究，对评定温度场品质，了解燃烧室内在规律，进而指导燃烧室的设计、加工具有重要意义。

1 多维度分析的理论基础

1.1 OLAP技术

联机分析处理（OLAP）的概念最早是由关系数据库之父E.F.Codd于1993年提出，它简单明确的定义是共享多维信息的快速分析。从多角度对信息进行快速、一致、交互地存取，从而获得对数据更深入了解的一种数据分析技术。OLAP技术的核心是“维”这个概念，“维”是人们观察客观世界的角度，是一种高层次的类型划分，“维”一般包含着层次关系，通过把一个实体的多项重要属性定义为多个“维”，使用户能对不同维上的数据进行比较[8]。本文借鉴OLAP技术的核心思想，将温度场数据按照不同的维度进行聚合和计算，进而输出多维数据视图，使数据能够被多角度、多侧面、多层次的考察，从而深入理解包含在温度场数据中的信息及内涵。

1.2 数理统计理论

数理统计分析适用于较多样本的数据分析，既可定性描述，也可定量推算，并可通过制作数据图表，直观地反映数据变化规律[9]。因此，采用数理统计分析研究温度场在不同维度中的特性和内在规律是一个有效途径。本文涉及的几个典型数理统计概念包括样本均值、样本均方差、相关系数等。

（1）样本均值X）杭囱救≈档钠骄笮 ？

（i=1，2.…，n，n≥2）

（2）样本均方差（s）：即样本与平均值的偏离程度，反映数据波动的大小。

（3）相关系数（ρ）：衡量两个随机变量之间线性相关程度的指标，相关系数ρ的值介于-1～1之间，ρ=0表示不相关，ρ的绝对值越大，表示相关程度越高。

（i=1，2，…n，n≥2）式中：cov（X，Y）为随机变量X，Y之间的协方差，DX，DY分别为随机变量X，Y的方差。

所谓相关是指事物或现象之间的相互关系，即当一个或几个相互联系的变量取一定数值时，与之对应的另一个变量的值虽然不确定，但仍按某种规律在一定范围内变化，变量间的这种关系被称为相关关系，因此，相关系数的大小也可以反映参与相关运算的两波形形状的相似程度[10]，例如，由n个点（X_i，Y_1i），i=1，2，…，n，n≥2确定的曲线1，与n个点（X_i，Y_2i），i=1，2，…，n，n≥2确定的曲线2，若两组点对应的横坐标X相同，则纵坐标数组Y_1i与Y_2i（i=1，2，…，n，n≥2）的相关系数就可以反映曲线1与曲线2的相似程度。

2 多维度分析的介绍

2.1 适用对象

本文采用的多维度分析法适用于有相对独立燃烧区的环形燃烧室，尤其是低污染燃烧室，其燃烧完全由头部决定，没有主燃孔空气，相邻两个头部的相互作用很弱，每个头部都对应一个相对独立的扇形出口温度场[11]。

本文以某环形直流燃烧室为例，对多维度分析方法进行介绍。该燃烧室在结构上呈轴对称，共12个头部，其出口溫度测量截面如图1所示，周向上均布三支温度探针，每支探针在径向上布置有5个温度侧点，位移机构每旋转3.75测量一次并记录数据，每支热电偶耙旋转120°，每个径向位置全环共测量96个点，5个径向位置一共测量480个点，根据头部位置将出口截面划分为12个扇形区域，则每个扇区共40个温度点（5×8）。

2.2 分析框架

根据OLAP的核心思想将温度场数据进行多维度的划分，包括整体、局部、微观、动态4个维度，并在各个维度中，根据温度场的特性，利用数理统计方法，对具体要素进行分析研究。

2.3 分析方法

对不同维度中具体要素的分析方法进行介绍。

2.3.1 整体维度

（1）全环温度场的特性参数

（a）对全环480个温度点取最大值、最小值及平均值;

（b）采用如下公式[12]对全环周向温度分布系数（OTDF）、径向温度分布系数（RTDF）进行计算。式中：T₃为燃烧室进口截面的平均总温，T₄，T_4max分别为燃烧室出口截面的平均总温以及最高总温。式中：T_4Rmax为燃烧室出口截面同一半径上各点总温，按周向取算术平均值后求得的最高平均径向总温。

（2）全环温度场的温度分布

为便于不同状态下温度分布曲线的对比分析，需将温度场数据进行无量纲化。例如，将燃烧室出口每个温度点（共480个）的值都减去出口平均温度即可得到无量纲化的温度值。

（a）全环周向温度分布曲线（无量纲）：根据径向位置的不同，可将全环480个无量纲化的温度点连成5条周向温度分布曲线，曲线的横坐标为周向位置，纵坐标为无量纲化的温度值。

（b）全环径向温度分布曲线（无量纲）：纵坐标为5个径向高度，横坐标为不同径向高度处对应的无量纲化全环平均温度。

（c）全环平均温度场的分布曲线（无量纲）：每个扇区对应有5行8列共40个位置点的无量纲温度值，分别取全环12个扇区中相同位置点无量纲温度的平均值得到扇区无量纲平均温度场（5×8个无量纲平均温度值），根据径向位置的不同，得到5条平均周向温度分布曲线（无量纲）。反映全环12个扇区温度场的基本形态。

2.3.2 局部维度

（1）扇区温度场的一致性

根据径向位置的不同将每个扇区中的40个温度值划分为5组（每组8个温度值），再将每个扇区中的这5组温度值分别和扇区平均温度场中对应的5组温度值求相关系数，根据2.2中的介绍，每个扇区得到的这5个相关系数值可以反映该扇区5条周向温度分布曲线和全环平均温度场中对应5条曲线的相似度，那么每个扇区中这5个相关系数的平均值越大（越接近1），说明该扇区的温度分布和扇区平均温度分布越相似，所有扇区相关系数的平均值越大，说明各个扇区的温度分布和平均温度场的温度分布越趋于一致，即全环温度场中各扇区的均匀性越好。

（2）扇区温度场的OTDF分布

（a）采用式（4）计算扇区的OTDF，其中T₄选用扇区的平均温度。

（b）根据式（1）、式（2）计算扇区OTDF的平均值和均方差，从而反映各扇区OTDF的分布特性。

（3）扇区温度场的径向温度分布

（a）扇区径向温度分布曲线：纵坐标为5个径向高度，横坐标为扇区中不同径向高度处对应的8个点的平均温度。

（b）扇区径向温度分布曲线的相关系数：采用式（3）得到各扇区中径向温度分布曲线和全环径向温度分布曲线的相关系数，从而定量地反映出各扇区径向温度分布的偏差程度。

2.3.3 微观维度

（1）扇区温度场的特性参数

（a）对每个扇区40个温度点求平均值、最大值及最小值。

（b）将每个扇区40个温度点按从大到小排列，进而求出前20%温度点的平均温度以及后20%温度点的平均温度。

（c）每个扇区40个温度点按径向位置分为5组，进而可求出每组中8个温度点的最大值，从而得到各扇区不同径向位置处的最高温度分布。

（d）将各扇区的特征参数分别求平均值和均方差，可得到各扇区特性参数的分布特性。

（2）扇区温度场的温度梯度

将各扇区中最高温度、前20%温度点的平均温度、扇区平均温度、后20%温度点的平均温度、扇区最低温度依次两两求差，可得到扇区温度场中不同温度层级的温度梯度。

2.3.4 动态维度

（1）温度场的变化

通过相关系数来定量分析同一个扇区在不同状态下温度场的变化程度。将每个扇区的温度点按径向位置的不同划分为5组（每组8个温度值），计算不同状态下温度场中相同径向位置处8个温度值的相关系数，可得到5个相关系数的值，其平均值的大小可反映该扇区温度场的变化程度。

2.4 分析结果

多维度分析的结果全部可以用EXCEL、MATLAB等工具以图表的形式输出，方便直观地了解温度场在各个维度中的分布特性，为后续对燃烧室部件试验结果进行大数据的挖掘分析提供思路和工具。

3 应用实例

为辅助说明多维度分析方法的内涵，以该直流燃烧室的A、B两组全环出口温度场数据为对象，对多维度分析的方法进行了举例说明。两组数据对应的试验工况相同，但火焰筒方案不同，其中A组数据对应原方案的火焰筒，B组数据对应火焰筒的Io点位置涡流器替换为改进型涡流器，其他零件状态都和原方案火焰筒相同。

（1）整体维度的分析

A、B温度场的全环特性参数见表1。

A组数据的全环无量纲周向温度分布曲线如图2所示。A、B温变场的全环无量纲径向温度分布曲线如图3所示。

A数据对应的无量纲全环平均温度场的周向温度分布如图4所示。无量纲全环平均温度场是12个扇区无量纲温度场的平均，反映了这12个扇區温度场的基本形态。

通过以上的分析，对全环温度场的特性参数、温度分布以及扇区温度场有了宏观的认识，并由此可进一步对比分析两个温度场总体特性上的差异。

（2）局部维度的分析

从图5中可以看出各扇区温度场的一致性以及出现差异的位置和程度，其中横坐标表示扇区的位置，纵坐标表示各扇区的平均相关系数。根据每个扇区中5条周向温度分布曲线和全环平均温度场对应的5条周向温度分布曲线（见图4）可求得5个相关系数，再求平均即可得到该扇区的平均相关系数，该数值越接近1，表示该扇区的温度分布和平均温度场的分布（见图4）越一致。A组数据对应温度场中，12#位置扇区的平均相关系数小于0.4，其余的都大于0.8，说明12#位置扇区的温度分布和其余位置的温度分布差异较大，因而可重点对该扇区进行分析研究。

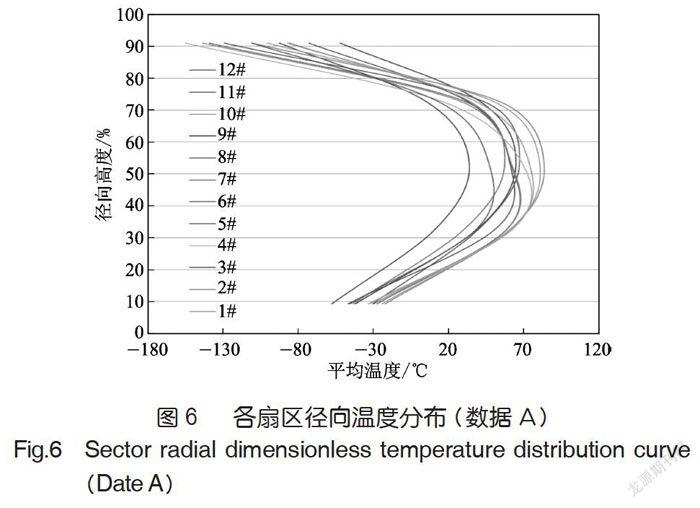
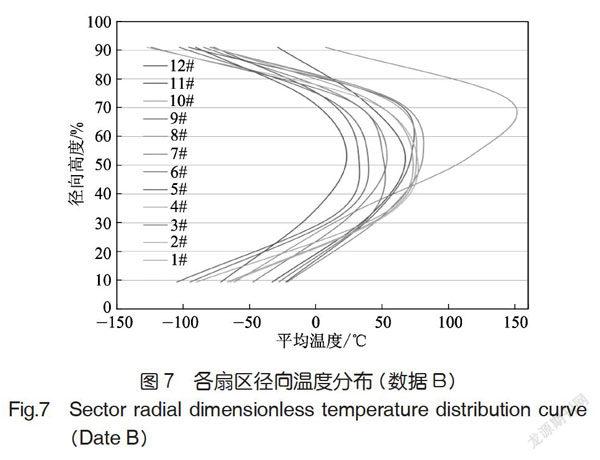
图6、图7中给出了A、B数据对应温度场的各扇区径向温度分布，从中可以看到10#位置更換改进型的涡流器后，其出口的径向温度分布发生了明显变化，因而可重点对该扇区的径向温度分布特性进行分析研究。

（3）微观维度的分析

从图8中可以看出A数据对应各扇区温度场的微观特性，即各扇区中的特性参数的分布，包括各扇区最高温度、最低温度、平均温度，前20%温度点的平均，后20%温度点的平均，同时通过对这些特征参数求差可以得到各扇区温度场中不同温度层级的温度梯度。

（4）动态维度的分析

该维度主要是通过相关系数来分析温度场的变化程度及位置。如图9所示，展示了数据A、数据B对应扇区温度场的相关系数，横坐标表示扇区的位置，纵坐标表示各扇区中周向温度分布曲线（5条）对应的相关系数（5个），从中可以看出，数据A、数据B在10#扇区位置对应的温度场的相关系数显著低于其余位置的相关系数，说明该区的温度场发生了较大变化，尤其是该扇区中T₄₁周向温度分布曲线的分布特征发生了显著变化，相关系数在0.4以下，而其余扇区的相关系数趋于1，说明其他扇区的温度场变化很小。这种分布规律符合燃烧室的状态变化，即只有10#位置更换了涡流器，其他零件状态不变，从而验证了该方法的有效性。

4 结论

本文借鉴OLAP技术的核心思想，采用数理统计理论，并根据温度场的分布特性，从整体、局部、微观、动态4个维度系统地介绍了燃烧室出口温度场的多维度分析方法，并以某燃烧室的出口温度场数据为例阐述了该分析方法的内涵，使该温度场数据被多角度、多侧面、多层次的考察分析，验证了该分析方法的有效性，可为摸索内在规律、改进优化方案、研究温度场对涡轮导叶影响等方面发挥作用，这有利于深入理解包含在温度场数据中的信息及内涵，并为后续对燃烧室部件试验结果的大数据挖掘分析提供思路和工具。

参考文献

[1]Lefebvre A H，Ballal D R.Gas turbine combustion alternativefuels and emissions [M].Philadelphia;Taylor Francis，2010.

[2]董素艳，刘松龄，朱惠人.进口热斑对涡轮级影响的非定常数值模拟[J].航空动力学报，2001，16（3）：242-248.

[3]Rai M M，Dring R P.Navier-stokes analysis of the redistributionof inlet temperature distortions in a turbine[R].AIAA，2002.

[4]林秀荣，丁毅生.燃烧室出口热点温度系数的确定[J].航空动力学报，1995，10（4）：426-428.

[5]刘富强，房爱兵，崔玉峰，等.回流环形燃烧室出口温度场的试验[J].航空动力学报，2012，27（1）：48-54.

[6]王兵，范玮，蔡士祥.某型涡扇发动机环形燃烧室温度场分布研究[D].西安：西北工业大学，2005.

[7]张树林，杨宝兴，王洪斌，等.航空发动机涡轮前温度场数据分析方法[J].航空发动机，2007，33（4）：23-27.

[8]范明，孟小峰.数据挖掘概念与技术[M].北京：机械工业出版社，2001.

[9]汪荣鑫.数理统计[M].西安交通大学出版社，2006.

[10]丁杨华，任勇.以相关系数为特征量的飞机目标识别法[J].清华大学学报：自然科学版，2001，41（7）：29-31.

[11] Hukan C.Mongia TAPS-A 4th generation propulsioncombustor technology for low emission[R].AIAA，2003.

[12]胡正义，江义军，赵清杰.航空发动机设计手册[M].第9册.北京：航空工业出版社，2000.