用MATLAB的模拟简谐振动合成探索
苏玉霞

摘 要:针对大学物理教学中简谐振动合成教学的难点,采用MATLAB软件对简谐振动进行合成模拟仿真,仿真分析同方向简谐振动合成,利萨如图形简谐振动合成,得到同向简谐振动合成曲线与互相垂直简写振动合成利萨如图,仿真结果表明,基于MATLAB的简谐振动合成结果具有良好的通用性、适用性,对于大学物理教学简谐振动合成视频再现,激发学生学习兴趣,提升课堂教学效果,提升人才培养质量。
关键词:简揩振动;MATLAB;模拟;利萨如图形
中图分类号:0415.5;TP391.9 文献标识码:A 文章编号:2096-4706(2018)02-0093-04
Simulation Analysis of Harmonic Vibration Synthesis Based on MATLAB
SU Yuxia
(Institute of Mechanical and Electrical Engineering,Longyan University,Longyan 364000,China)
Abstract:Aiming at the difficulty of harmonic vibration synthesis teaching in college physics teaching,the MATLAB software is used to simulate the simple harmonic vibration,and the simple harmonic vibration synthesis in the same direction is simulated,lissajous figure synthesis of harmonic vibration,the results show that the synthetic results of simple harmonic vibration based on MATLAB have good universality and applicability,and the results of harmonic vibration synthesis in college physics teaching,stimulate students' interest and improve the effect of classroom teaching. Improve the quality of talent training.
Keywords:simple harmonic vibration;MATLAB;simulation;lissajous figure
0 引 言
振動是物体的一种普遍的运动形式,并不限制在机械运动范围。它不仅是声学、地震学,建筑学、机械制造等必需的基础知识,也是电学、光学、无线电学的基础[1]。简谐振动是振动最简单也是最基础的振动形式。这部分教学内容中,简谐振动的合成较抽象,既是重点也是难点。虽辅以示波器实验进行观察,但学生们还是难以理解。MATLAB是一种工具软件,具有强大的科学计算与图形处理能力。因此,采用MATLAB数值计算的方法模拟简谐振动的合成,并进行进一步探索,形象地显示同方向简谐振动合成时的主周期、“拍”以及利萨如图的形成。
1 简谐振动合成理论
1.1 同方向简谐振动的合成
假设一质点同时参与两个机械振动,为了突出频率f的不同效果,设两个振动振幅相同,且初相设为0。两个机械振动分别为:;,合振动为。
(1)当与不太大时:合振动x虽然不是简谐振动,但却是周期性的运动,其周期(即主周期)T是分振动周期的最小公倍数。
(2)当与比较大,且 时:合振动x振幅呈现周期性变化形成“拍”。
1.2 互相垂直,不同频率简谐振动的合成——利萨如图(Lissajous' figures)
假设一质点同时参与x,y两个互相垂直、不同频率的机械振动。一般来说,在互相垂直的分振动频率不同的条件下,合振动的轨迹不能形成稳定的图案,但如分振动频率成整数比,则合成振动的轨迹为稳定的曲线,曲线的花样和分振动的频率比、初相位有关,得出的图形叫利萨如图(Lissajous' figures)[2]。
两个互相垂直、不同频率的简谐振动分别是:
;
利萨如图形仅与分振动的频率比、初相位有关,因此可选定分振动的圆频率分别为:与,α为二个分振动的初相差。
2 同方向简谐振动合成的MATLAB模拟
,,合振动
MATLAB模拟同方向简谐振动合成,模拟程序Ⅰ如图1,首先输入参数、及振幅A的值。
程序Ⅰ
(1)当与不太大,同方向简谐振动合成模拟。程序Ⅰ运行窗口如图2。
图3显示,当T1=2S、T2=3S,合振动是主周期T=6S的非简谐周期性运动。
(2)当与比较大,且 程序Ⅰ运行窗口如图4。“拍”的形成,同方向简谐振动合成模拟,如图5。
3 利萨如图形的MATLAB模拟——互相垂直,不同频率简谐振动的合成
;
程序中取,y,x二分振动圆频率比分别为几个整数比值,且初相差α分别对应取一系列值时的利萨如图。模拟程序Ⅱ如图6。
程序Ⅱ
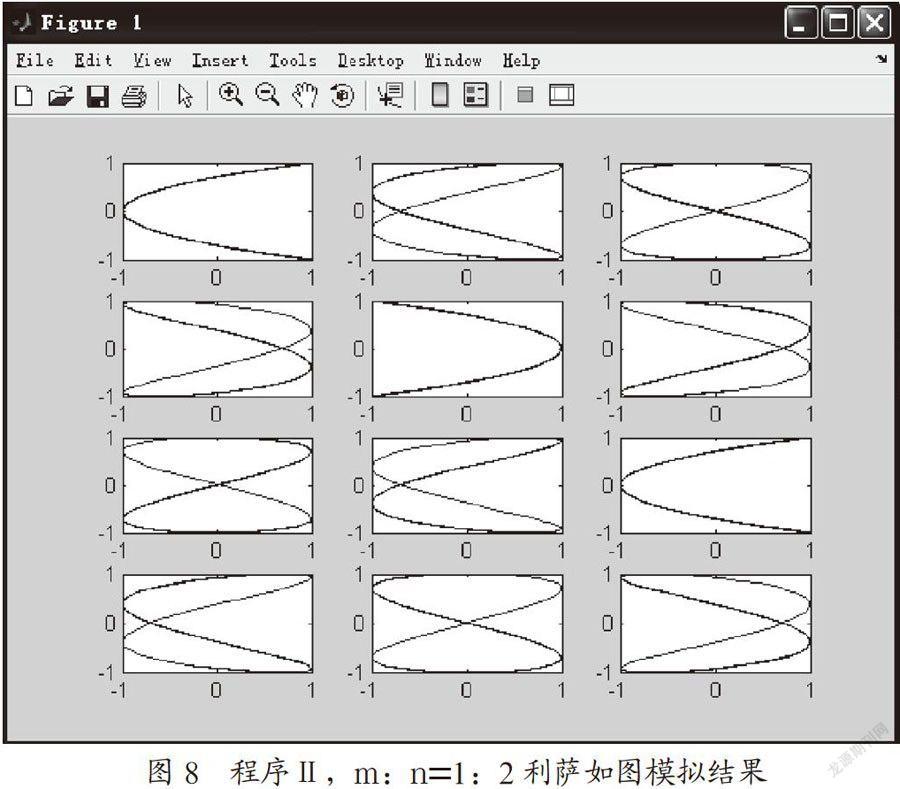
(1)输入y,x二分振动圆频率比为1:2时,参数如图7所示,模拟结果如图8所示。
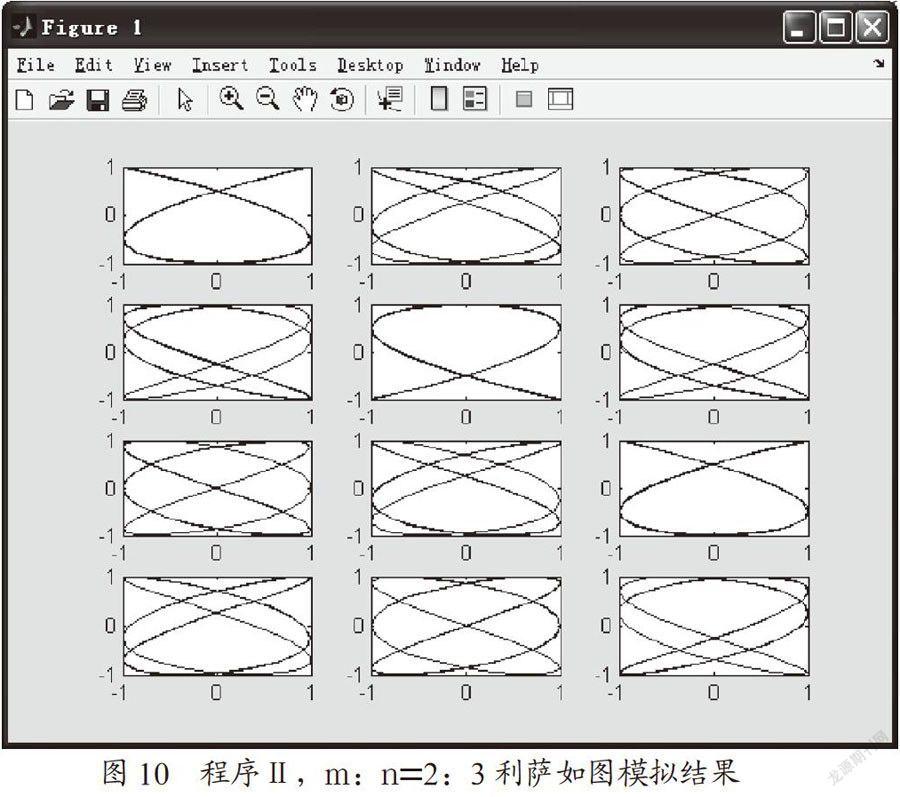
(2)输入y,x二分振动圆频率比为2:3时,参数如图9所示,模拟结果如图10所示。
(3)输入y,x二分振动圆频率比为4:5时,参数如图11所示,模拟结果如图12所示。
互相垂直,不同频率简谐振动的y,x二分振动圆频率比m:n为其它任何比值时的模拟还可以通过在执行程序时,输入参数的改变来进行。而可以通过程序Ⅱ的k循环变量的终值增大,来增加对应一个m:n比值下的初相差α的取值个数。
示波器实验,对应互相垂直的二分振动圆频率比m:n,观察到的利萨如图,不是唯一的,会随着时间发生缓慢变化,而且与图8、图10、图12等完全一致。
4 结 论
文章借助MATLAB对简谐振动进行了模拟。演示了同方向二分振动合成为非简谐周期性运动及“拍”的形成,详细研究了相互垂直二分振动合成的利萨如图形。在大学物理教学中,采用文中方法讲授简谐振动的合成,学生反应良好。
一方面促进了学生对物理知识的理解,另一方面调动学生对计算机语言的学习热情,学生的计算机运用能力得到提高。简谐振动的MATLAB模拟,能给人实验情境的感受,激发学生的学习兴趣,调动学生的学习积极性,活跃课堂气氛。既能使学生自己上机进行实验模拟,又能作为理论教学的课堂演示课件,具有一定的推广价值。
参考文献:
[1] 赵近芳.大学物理学(上) [M].北京:北京邮电出版社,2010:124.
[2] 漆安慎,杜婵英.力学 [M].高等教育出版社,1997:383.

