水文模型模拟水文极值的不确定性分析

王思媛 胡高辉 孙利敏 陈浩 杨涛

摘要：以黄河源区为研究区，运用GLUE法分析了HBV模型和新安江模型模拟水文极值的不确定性。目标似然函数阈值分别选用0.7、0.6、0.5，将得到的洪水和枯水水文极值以及选出的模拟结果按丰水年、平水年和枯水年过程分别进行分析。结果表明：两个模型均擅长于模拟洪水，而且时洪水模拟的不确定性较对枯水模拟的不确定性低；从两个水文模型模拟日过程估计区间的差别看，HBV模型估計区间与实测相比，洪水年总体偏低，枯水年总体偏高，平水年不存在明显趋势，新安江模型则不存在这个特点；在相同的参数采样方法和策略下，HBV模型的不确定性比新安江模型更显著；两个水文模型对枯水指标Q9o和Q7s模拟的不确定性都较大；新安江模型对洪水指标Qu和QIa的估计区间小于HBV模型的，不确定性水平较低。

关键词：HBV模型；新安江模型；GLUE法；不确定性分析；水文极值；黄河源区

中图分类号：P333；TV882.1 文献标志码：A doi：10.3969/j.issn.1000-1379.2018.02.001

黄河源区位于青藏高原东北部，属于典型的高原寒区，对气候变化的响应非常敏感，已经成为国内外气候变化研究的热点区域之一。黄河源区水文模型的应用研究也受到很多人关注。同时，人们开始重视水文模型引起的不确定性研究。许慧萍[1]运用TANK模型，对考虑季节性冻土的黄河源区径流特征进行了模拟，提出了适合黄河源区的概念性降雨径流模型，采用TANK模型和融雪模型及冻土运移模型相结合的方法进行模拟，达到了预期效果；刘昌明等将SWAT水文模型应用于黄河源区，模拟了1986-1995年和1963-1997年的径流量，并运用1986-1995年唐乃亥水文站实测水文资料进行了验证，结果表明SWAT模型可应用于黄河源区。本文运用新安江模型和HBV模型对黄河源区径流过程进行模拟，并采用GLUE方法对比了两个模型对黄河源区水文极值模拟的不确定性。

1 研究区概况

黄河源区（指黄河源头到唐乃亥水文站之间的区域）控制面积为12.2万km2[2-3]，地势西高东低，平均海拔4000m[4]，是典型的高寒气候区。黄河源区年际气温差异小，日温差较大，日照时间长，辐射强烈。受西南季风影响明显，年降水量为250～750mm，降水量年际变化大，年内分配不均，降水主要集中在6-9月（占全年降水量的75%～90%）。源区多年平均径流量为204.17亿m3，以降水和冰雪融水补给为主，占黄河多年平均径流量的38.15%[5-6]。黄河源区主要有4个水文站，从上游到下游依次为黄河沿、吉迈、玛曲和唐乃亥，因此流域依次被4个水文站划分为4个子流域。

2 研究方法

2.1 HBV模型

HBV（Hydrologiska Byrans Vattenbalansavdelning）模型是一种半分布式概念性水文模型，最初由瑞典气象组织（SMHI）于20世纪70年代初创建[7-8]。模型发展之初是为了径流模拟和水文预报[9]，由于模型输入资料较为简单，应用便捷，因此发展较为迅速，目前已在40多个国家和地区得到应用[9-11]。在该模型中，通过把流域划分成不同子流域进行模拟，不同的子流域又可以根据海拔、土地利用和土壤类型等进一步划分[7，12]，在每个子流域内计算积雪/融雪、土壤湿度以及径流过程等。由图1可以看出，资料输入后主要通过积雪/融雪模块、土壤模块、响应模块和路径模块4部分[8]进行计算。

2.2 新安江模型

河海大学赵人俊教授在编制新安江洪水预报方案时，设计完成了国内第一个比较完善的流域水文模型——新安江模型。模型发展之初是二水源模型，到20世纪80年代中期，借鉴山坡水文学的概念和国内外产汇流理论，提出了三水源新安江模型。由于该模型采用的是蓄满产流概念，因此主要适用于湿润半湿润地区，但目前也有将其应用于半干旱的黄河、海河等流域的实例[13-14]。

三水源新安江模型的蒸散发计算采用三层模型，产流计算采用蓄满产流模型，用自由水蓄水库结构将总径流划分为地表径流、壤中流和地下径流三部分，流域汇流采用线性水库，河道汇流采用马斯京根分段连续演算或滞后演算法[15]。

新安江模型是分布式模型，它把全流域分成许多单元流域，对每个单元流域进行产汇流计算，得到单元流域的出口流量过程。再进行出口以下的河道洪水演算，求得流域出口的流量过程。把每个单元流域的出流过程相加，即可求得流域出口的总出流过程。

2.3 GLUE方法

GLUE方法由Beven K.等[15]于1992年提出，用于分析和评价异参同效现象。GLUE方法的思想是模型参数的好坏不是由单个参数决定的，而是由一组参数决定的[16-18]。其主要方法：在设定好的参数范围内按Monte-Carlo随机抽样方法选择参数，选择效率系数为目标函数，将不同参数组成的参数组合代入模型中计算，可以得到对应每组参数的效率系数值，得到的所有效率系数值定义为似然目标函数值。在所有的似然目标函数值中设定一个临界值，该值的选择由人为决定，低于该临界值则表示其参数组合不能表征模型的结构，对这些参数组合的似然值可以直接赋值为0，计算不确定性时直接忽略不计。按照似然值的大小，求出某个置信度水平下模型的不确定性范围。GLUE方法分析的主要步骤为：①似然判据的定义；②确定参数的初始范围和先验分布函数；③不确定性分析；④似然函数值的更新。

3 基于GLUE方法的水文模型不确定性分析

3.1 HBV模型不确定性分析

采用GLUE方法进行分析，目标似然函数阈值分别选用0.7、0.6、0.5，将得到的洪水和枯水水文极值（保证率分别为10%、25%、75%、90%，置信度为95%）以及选出的模拟结果按丰水年、平水年和枯水年过程分别分析，见图2～图4。由图2～图4可知：①似然函数阈值为0.7时，典型丰水年HBV日模型的不确定性区间可以将实测过程线基本包住，即在阈值较高的时候就可以很好地模拟实测过程，不确定性较低，阈值分别为0.6、0.5时，不确定性区间扩大，不确定性增加；②阈值为0.7时，典型平水年实测流量过程大部分落在不确定性区间内，仍有一部分落在区间外，当阈值减小时不确定性区间扩大，实测过程线也逐渐被不确定性区间包围；③阈值为0.7时，典型枯水年实测过程线大部分在不确定性区间外，随着阈值的减小，实测流量过程线逐渐被不确定性区间所包围，但是模型在模拟枯水年时的不确定性区间较实测值大很多，即虽然不确定性区间将实测过程线包住了，但实测流量过程线在区间下方，不确定性区间较实测流量值的变化范围大；④当阈值为0.7时，HBV日模型模拟的年枯水指数Q90（流量保证率为90%）的不确定性区间效果很差，阈值降为0.6时有一部分实测极端枯水值落在模拟不确定性区间内，阈值降至0.5时大部分实测极端枯水值都落在不确定性区间内；⑤阈值为0.7时枯水指数Q90和Q75的不确定性区间类似，但Q75比Q90模拟的不确定性减小，不确定性区间随着阈值减小逐渐扩大并包住了实测枯水极值，不确定性增加；⑥阈值为0.7时洪水指数Q25模拟的不确定性水平比枯水指数Q75的低，大部分实测洪水极值落在不确定性区间内，这表明模型对极端洪水Q75具有一定模拟能力，阈值为0.6时Q25的不确定性区间扩大，阈值为0.5时即可将实测极端洪水过程绝大部分包住；⑦阈值为0.7时洪水指数Q10模拟的不确定性水平和Q25的类似，即不确定性区间能在一定程度上包住实测洪水过程，但Q10的实测洪水过程的后半部分在不确定性区间下部，这种情况同样出现在阈值为0.6和0.5时。

3.2 新安江模型不确定性分析

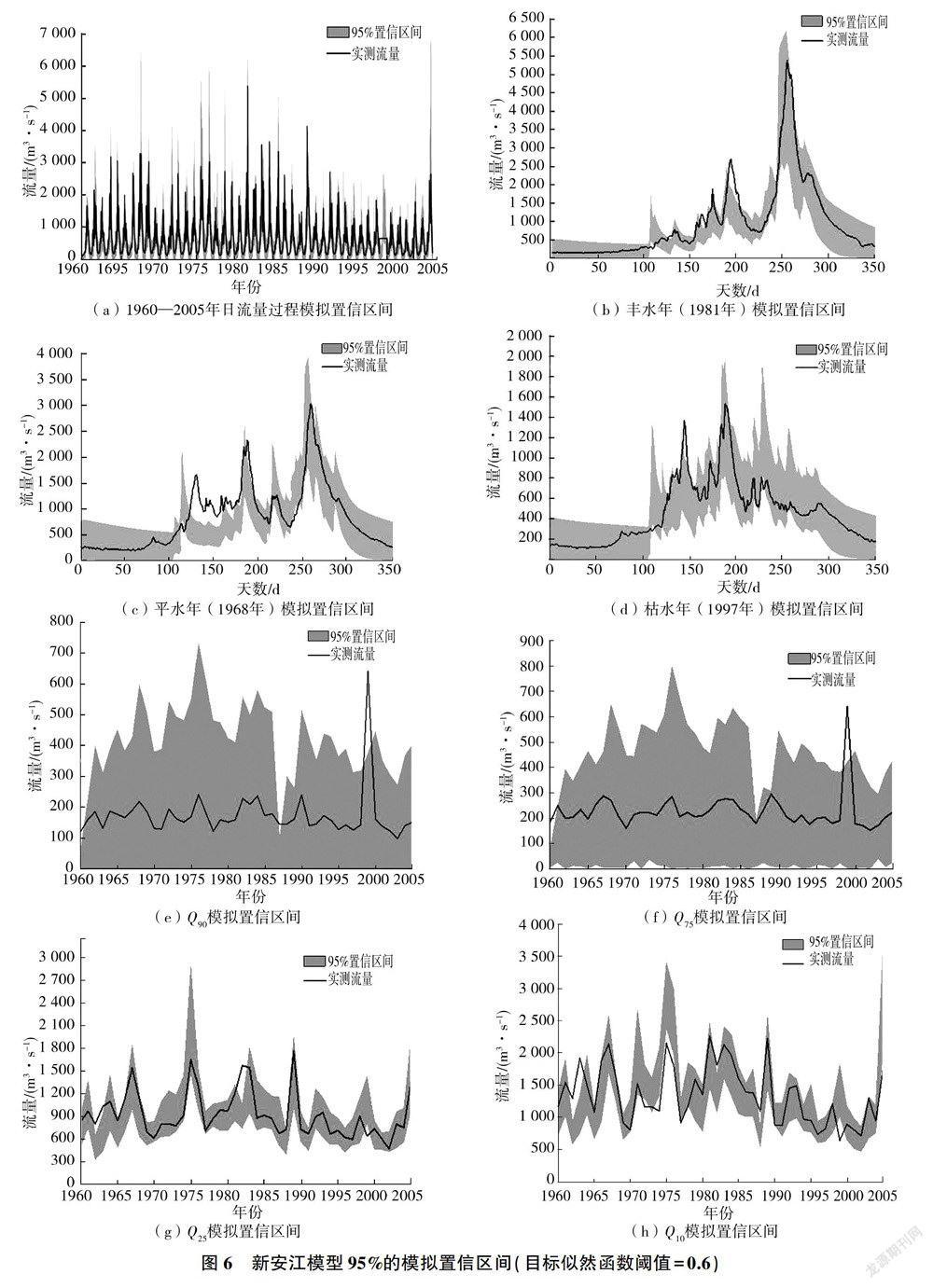
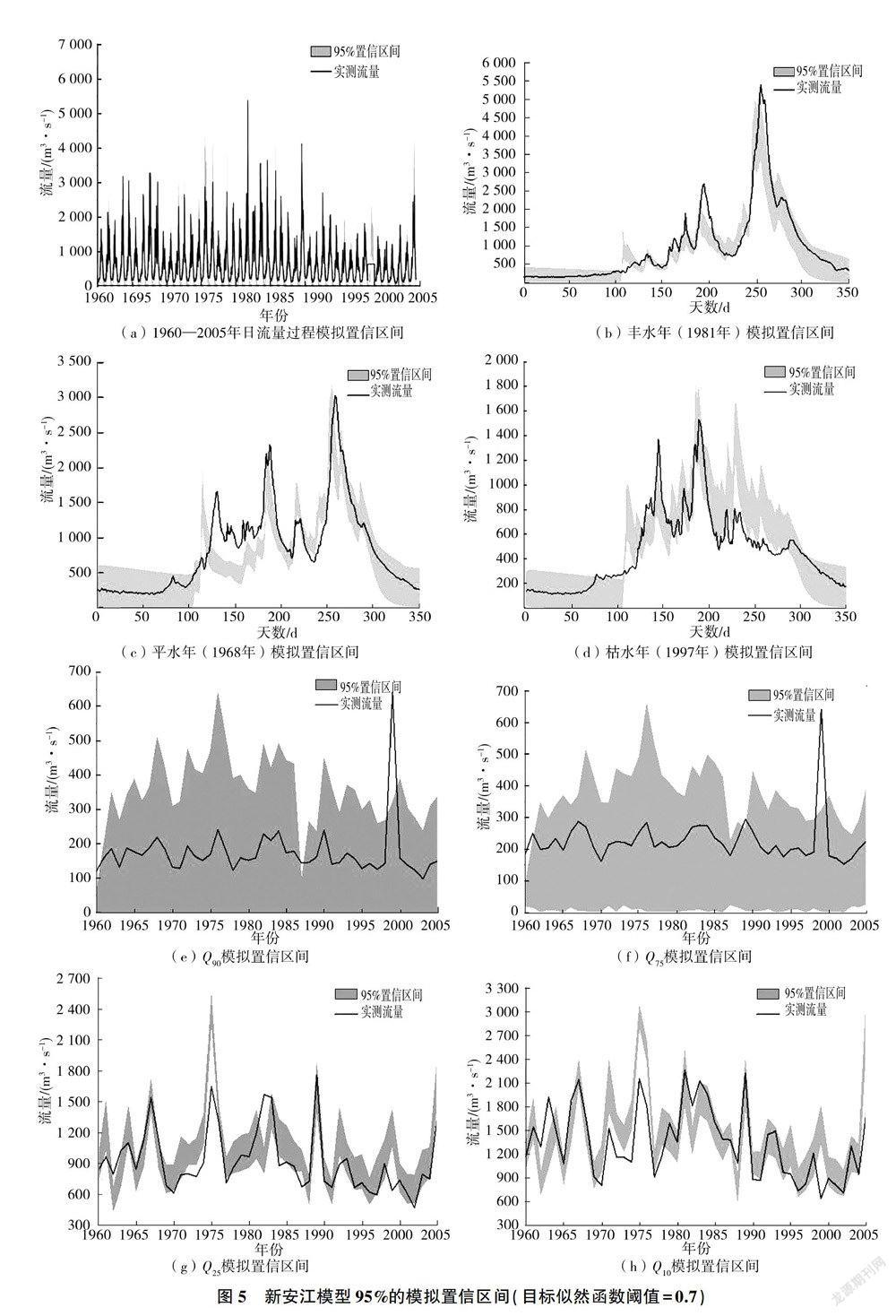
由图5～图7可知：①随着阈值的降低，新安江模型对典型洪水年的模拟效果越来越好，阈值为0.5时可以很好地模拟典型洪水年的实测流量过程；②阈值为0.7时典型平水年低水（流量较小）部分在不确定性区间内，高水（流量较大）部分大都在不确定性区间外，阈值为0.6时大部分高水部分进入不确定性区间内，但还是有一部分在不确定性区间外，阈值为0.5时还有一部分在不确定性区间外，但是比阈值为0.7、0.6时小了很多，这说明模型对平水年的模拟效果不好；

③阈值为0.7时典型枯水年除了部分低水在不确定性区间内，大部分在不确定性区间外，阈值为0.6时还有一部分在不确定性区间外，但明显比阈值为0.7时少了很多，阈值为0.5时大部分实测流量过程线落到不确定性区间内，这说明阈值越小模型模拟能力越强，同时不确定性也提高了；④阈值为0.7时年枯水指数Q90的不确定性区间基本可以把实测极端枯水过程线包住，表明模型可以模拟该实测过程且不确定性较低，随着阈值的减小，模型模拟的不确定性增大；⑤与Q90相比，不同阈值条件下年枯水指数Q75的不确定性区间较大，但不确定性减小，阈值为0.5时Q75的不确定性区间虽然可以将实测过程线基本包住，但是不确定性增大很多；⑥洪水指数Q25模拟的不确定性比枯水指数Q75的低，阈值为0.7时不确定性较低，但是大部分实测流量过程在不确定性区间外，阈值降为0.6时不确定性升高，实测极端洪水过程大部分在不确定性区间内，阈值降为0.5时不确定性继续提高，实测极端洪水过程绝大部分落在不确定性区间内；⑦洪水指数Q10模拟的不确定性水平和Q25的类似，模拟效果相差不大，即不确定性区间小的时候实测极端洪水过程线在不确定性区间外，当不确定性升高时实测洪水过程线逐渐落到不确定性区间内。

4 结语

（1）两个水文模型对枯水指标（Q90和Q75）的估计区间都远大于洪水指标（Q25和Q10）的，这表明上述模型均擅长模拟洪水，而且对洪水模拟的不确定性较枯水模拟的低。另外，通过对水文极值的不确定性进行对比，发现新安江模型的不確定性水平更低。

（2）GLUE方法估计的不确定性区间对目标似然函数阈值较为敏感，当目标似然函数阈值较大（0.7）时，两个水文模型的估计区间都比当目标似然函数阈值较小（0.6和0.5）时的估计区间窄，不确定性水平低。但是，当目标似然函数阈值高时估计区间窄，不确定性水平低，误差区间减小，但会增加两个水文模型出现实测值落到估计区间之外的可能性，即对出口断面的模拟并不理想。

（3）不确定性分析方法和理论仍有待改进。本文采用了GLUE方法进行模型不确定性分析，然而该方法也存在缺点，如选择目标似然函数的阈值过于主观，和标准的贝叶斯不确定性分析方法存在一定差异等。另外，目前习惯采用模型效率系数为目标似然函数进行不确定性分析，指标过于单一，建议今后研究采用不同的指标（如均方根误差、相对误差等）或综合指标作为目标似然函数进行不确定性分析的效果，从不同角度反映模拟的误差特征。

（4）水文极值事件的模拟和预测理论有待改进。目前水文极值的模拟预测方法大部分是沿用常规的水文模型，然后对其模拟预测结果进行极值分析。存在的缺点：①通常以模型效率系数最佳为目标函数率定模型参数，往往会降低对水文极值的模拟效果；②对特大洪水的形成机理和枯水期间基流的维持机理缺乏深入了解，从而影响洪水（枯水）极值的模拟效果，制约水文极值模拟理论的发展。建议加强野外观测和室内试验，结合现代数值模拟技术，深入研究水文极值事件的形成和维持机理，为改进水文极值的模拟方法提供理论支撑。

参考文献：

[1]许慧萍.考虑季节性冻土的黄河源区流域水稳TANK模型[D].北京：中国地质大学，2009：14-24.

[2]陈利群，刘昌明，郝芳华，等.黄河源区气候对径流的影响分析[J].地学前缘，2006（5）：321-329.

[3]孙贵山.黄河源区降水径流变化特性初步分析[J].水资源研究，2008，29（3）：22-25.

[4]LI L，HAO Z C，WANG J H，et al.Impact of Future ClimateChange on Runoff in the Head Region of the Yellow River[J].Journal of Hydrologic Engineering，2008，13：347.

[5]郝振纯，李丽，张磊磊，等.GCMs模式在黄河源区的适用性分析[J].河海大学学报（自然科学版），2009，37（1），7-11.

[6]牛玉国，张学成.黄河源区水文水资源情势变化及其成因初析[J].人民黄河，2005，27（3）：31-33.

[7]DAS T，BARDOSSY A，ZEHE E，et al.Comparison of Con-ceptual Model Performance Using Different Representationsof Spatial Variability[J].Journal of Hydrology，2008，356（1-2）：106-118.

[8]LINDSTR M G，JOHANSSON B，PERSSON M，et al.Devel-opment and Test of the Distributed HBV-96 Hydrological Model[J] .Journal of Hydrology，1997，201（1-4）：272-288.

[9]张建新，赵孟芹，章树安，等.HBV模型在中国东北多冰雪地区的应用研究[J].水文，2007，27（4）31-34.

[10]ARHEIMER B，LIDEN R.Nitrogen and Phosphorus Con-centrations from Agricultural Catchments-Influence ofSpatial and Temporal Variables[J].Journal of Hydrology，2000，227（1-4）：140-159.

[11]LIDEN R，HARLIN J.Analysis of Conceptual Rainfall-Runoff Modelling Performance in Different Climates[J].Journal of Hydrology，2000，238（3-4）：231一247.

[12]赵人俊.流域水文模拟：新安江模型与陕北模型[J].北京：水利电力出版社，1984：106-130.

[13]李致家，孔凡哲，王栋，等.现代水文模拟与预报技术[M].南京：河海大学出版社，2010：1-61.

[14]张洪刚，郭生练.概念性水文模型多目标参数自动优选方法研究[J].水文，2002，22（1）：12-16.

[15]REVEN K，FREER J.Equifinality，Data Assimilation，andUncertainty Estimation in Mechanistic Modelling of ComplexEnvironmental Systems Using the GLUE Methodology[J].Journal of Hydrology，2001，249（1-4）：11-29.

[16]张利茹，管仪庆，王君，等.GLUE法分析水文模型参数不确定性的研究[J].水力发电，2010，36（5）：14-16.

[17]卫晓婧，熊立华.改进的GLUE方法在水文模型不确定性研究中的应用[J].水利水电决报，2008，29（6） ：23-25.

[18]AN X，XU CY，ZHANG Q，et al.Parameter and ModelingUncertainty Simulated by GLUE and a Fonnal BayesianMethod for a Conceptual Hydrological Model[Jl .Journal ofHydrology，2010，383（3-4）：147-155.