泥浆管道输送特性的CFD模拟
熊庭 张梦达 危卫 安邦

摘要:为防止挖泥船施工中泥浆泵能耗高、输送阻力大和排泥管道淤堵,以水平管道中泥浆流动过程为研究对象,采用以颗粒动力学为基础的欧拉双流体模型,对水平管道中泥浆输送的固液两相流进行了CFD数值模拟,并与Durand模型的计算值和文献中的试验数据进行了对比。结果表明:数值模拟得到的计算结果与实测值表现出良好的一致性;在管道内充分发展段,管道截面的垂直中心线上颗粒浓度呈不对称分布,并且不对称度随着颗粒浓度增大或泥浆流速变大而降低;粗颗粒在管道底部由于受到升力作用,因此其浓度曲线在管道底部近壁处出现反折;CFD模型得到的压降计算值较Durand模型更接近实测值。
关键词:欧拉双流体模型;Durand模型;FLUENT;固液流;流动特性;管道输送;泥浆
中图分类号:0359;TV134
文献标志码:A
doi: 10.3969/j.issn.1000-1379.2018.04.005
泥浆管道输送具有高效性和经济性,在围海造陆、航道开辟、湖泊清淤等领域得到了广泛应用。研究固液两相流在管道中的流动特性、固体颗粒的动力学特性和管道输送的阻力特性,并据此优化输送参数,对于提高管道输送浓度、降低管道输送阻力、避免管道堵塞及延长输送距离具有重大意义。泥浆管道输送中的重要设计参数有颗粒浓度分布、压降、沉积速度等。研究者们以大量的试验数据为基础,提出了一系列方法来预测这些参数,如Durand模型、Wasp模型等。这些经验公式在实际T程中应用广泛,但限制条件严格,若对特定的T况模型选择不当,则会出现很大的计算误差。随着计算流体力学( Computational FluidDynamiCs,CFD)和计算机模拟技术的发展,CFD方法在管道固液两相流研究中的应用越来越普及,目前主要的模型有以离散单元法为基础的拉格朗日模型、把固体颗粒作为拟流体的欧拉模型以及Ling等提出的ASM(代数滑流混合模型)。张宏兵等运用ASM模型对携沙水或油的两相流特征进行了数值模拟,发现主流速度最大值点随浓度增加而向管道底部运动,主流速度降低时管道横截面内颗粒浓度向下和向两侧增大。但是,ASM模型仅适用于低Stokes数的情况,且对固相体积分数分布的预测不够准确。陈建宏等利用Fluent软件对质量分数为78%的浆体输送特性进行了仿真计算,得出了该浆体阻力损失随流速变化的关系式。但是,目前关于输送工况和管道参数对泥浆输送特性影响的研究还较为缺乏。
鑒于此,本文利用以颗粒动力学为基础的欧拉双流体模型,建立了水平管道中泥浆固液两相流的三维CFD模型,通过Fluent软件求解数学模型,研究管道内泥浆输送的流动特性,以分析输送速度、泥浆浓度、颗粒粒径等对输送特性的影响。
1 数学模型
1.1 欧拉模型
欧拉模型假设泥浆流由固相和液相组成,固相“s”也被视为一个连续相,与液相“l”一样占据一定的空间,则χs+χ1=100%,其中χs和χ1分别为固相和液相的体积浓度。固相和液相均满足质量守恒和动量守恒两大定律,相与相之间通过压强和相间交互系数耦合起来:式中:t为时间;χi为各相的浓度;▽2为拉普拉斯算子;pi为各相的密度;vi为各相的速度。
液相动量方程为
固相动量方程为式中:T1和Ts分别为液相和固相的剪切应力张量;g为重力加速度;p为流体局部压力;Ksl为固液两相间动量交换系数。
1.2 湍流模型
k一δ模型把湍流黏性与湍流动能联立,建立了两者与涡黏性的关系,被广泛运用到流场模拟计算中,其湍动能k的输运方程为式中:utm为混合物湍流黏度;Gkm为湍动能生成项;pm为混合物密度;k一δ模型中各系数的取值分别为σk=1.0,σg= 1.3, Cls= 1.44, C2k= 1.92.
1.3 两相流中泥沙受力模型
泥沙颗粒在泥浆管道中受到的力主要包括重力、曳力(由颗粒与流体间相对运动引起的阻力)、虚拟质量力、升力(由液相速度梯度或颗粒尺寸大于黏性次层所产生)、壁面润滑力、湍流耗散力(由湍流旋涡与相间曳力相互作用引起,倾向于将固相从高浓度区扩散至低浓度区)、Magnus力和Saffman力。其中:曳力和湍流耗散力是影响固相和液相间动量传递的主要作用力。为保证模型计算的准确性与高效性,以及更精确地获得颗粒在近壁面处的浓度分布,本文在后述的研究中同时考虑曳力、升力和湍流耗散力。
2 仿真实例
2.1 物理模型
在ICEM CFD中建立内径D=50、103、900 mm,长度均为60D的水平管道。模型中建立了25层的边界层,增长比率为1.2,以提高壁面函数的求解表现。管道网格的横断面如图1所示。液相物性:密度p1=997k/m3,动力黏度μ1= l.005xl0-3 Pa·s;固相基本物理参数及计算工况见表1。
2.2 边界条件与求解方案
人口:速度人口,速度和每相的体积分数都指定为具体值。出口:压力出口,压强设定为大气压。管壁:壁面采用无滑移条件。采用商业CFD软件Fluent求解上述边界条件和湍流模型的方程组,残差值类型为均方根残差值,收敛残差均选取10-5。为确保足够精确、稳定和迭代过程收敛,动量方程求解中采用QUICK方法,其他方程均采用二阶迎风方法。
3 Durand模型
Durand模型将两相流的阻力损失Jm表示为清水阻力损失Jo和附加阻力损失Js两部分之和,即式中:K为模型系数,在标准Durand模型中取180;Cv为颗粒体积浓度:w为颗粒沉降速度;d50为中值粒径;λ为清水沿程阻力系数;v为浆体流速。
4 结果与分析
图2为Al工况下沿管道轴向八等分处各横断面垂直中心线上的颗粒速度曲线和体积浓度曲线。其中纵坐标y为无量纲垂直位置(y= y/D,即在管道中的高度与管径之比,其值在管道顶端为1,底部为0)。由图2可知,第1到第3个截面上的颗粒流速和体积浓度均发生了明显变化,第4到第8个截面位置的曲线已几乎一致,故在这个区域管道内流态得到了充分发展。为保证分析结果的准确可靠性,后述的体积浓度和速度模拟值在管道出口处获得,压力监测断面选在管道出口和距出口1m处截面。
4.1 颗粒体积浓度分布
颗粒体积浓度分布是泥浆管道输送中预测管道磨损的重要因素,管道中固体颗粒的浓度分布规律与许多因素都有关,如泥浆浓度、泥浆流速、管道直径、颗粒粒径等。图3和图4分别为粒径dp=90、270 μm的泥浆在管径103 mm管道中流动时的颗粒体积浓度模拟值与R.G.Gillies等实测值的对比,可以看出模拟值与实测值表现出良好的一致性。图5和图6分别为Al、Bl 工况下颗粒体积浓度分布云图,可以看出颗粒在水平方向上几乎呈对称分布,在垂直方向上表现为上半部分浓度较低,下半部分浓度较高。当颗粒浓度增大时,可以观察到体积浓度曲线的对称度升高,原因是颗粒体积浓度增大后增强了颗粒间运动的相互影响作用。对于较大粒径(270μm)的颗粒,在管道底部的近壁面处观察到体积浓度曲线出现了反折,即近壁面处颗粒浓度降低,最大浓度点上移,在试验中该区域的数据并未采集到。这主要与前面提到的近壁面升力有关,由于颗粒的粒径大于黏性次层厚度,因此在液相中受到剪切力而产生了垂直于相对运动方向的运动。
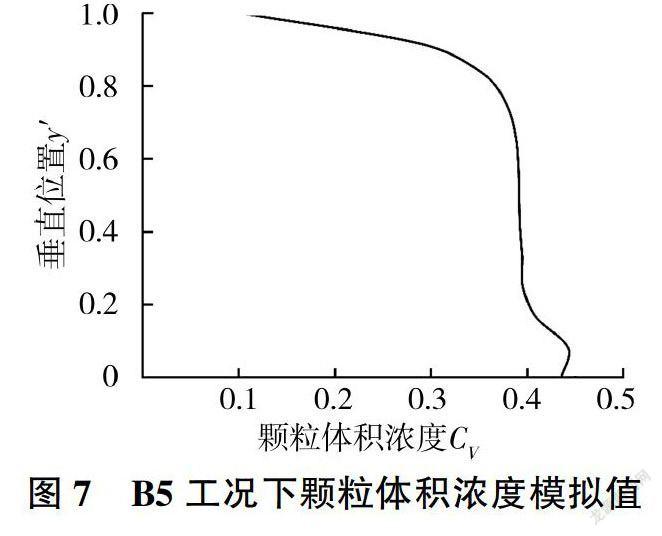
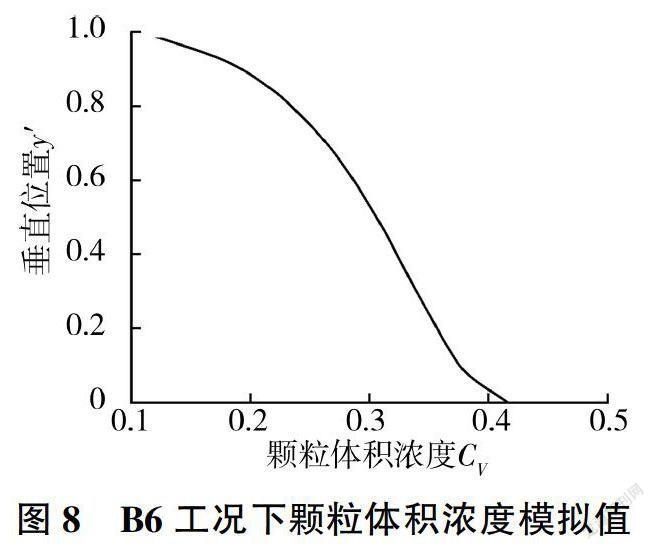
图7为B5 工况下垂直中心线上颗粒体积浓度的模拟值,与B4 工况相比流速降低为1.8 m/s,y ≤0.1区域的浓度曲线反折程度降低,颗粒体积浓度明显变大,其原因可能是流速降低后管道内湍流强度降低,导致升力降低。图8为B6 工况下颗粒体积浓度的模拟值,与B3 工况相比可以看出,管道内径增大为900mm,在管道底部浓度曲线没有出现反折,最大浓度点在管道最底部,原因是随着管径的增大,临界流速增大,颗粒沉降运动的影响增强,而升力对泥沙颗粒的作用相对变弱,在沉降作用的主导下浓度最大点出现在管道的底部。
图9为粒径440μm的泥浆在管径50mm管道中流动时的颗粒体积浓度曲线,可以看出在垂直中心线上,颗粒体积浓度呈不对称分布,随着流速增大,體积浓度曲线的对称度升高,原因是泥浆的湍动会引起颗粒悬浮,而混合物流速越大流体湍动能越大。
4.2 速度分布
由图10、图11可知,Al 工况下模拟值与实测值符合较好,泥沙颗粒速度在水平和垂直方向上都接近于对称分布。
图12为粒径为270μm、体积浓度分别为0.1、0.2、0.3的泥浆在垂直中心线上颗粒速度的分布曲线,可以看出速度呈不对称分布,且不对称度随着颗粒浓度的增大而变大。结合图4中270μm颗粒的浓度分布曲线可知,随着泥浆浓度增大,管道下半部的泥沙颗粒变得更多,使得管道下部颗粒运动的阻力增大。图13为不同流速下粒径440μm的泥浆在垂直中心线上颗粒速度的分布曲线,可以看出速度近似呈对称分布,速度最大点在管道中心,其原因可能是440μm粗颗粒受重力的影响更大,向下运动的速度分量变大,粗颗粒在管道底部受到更大升力使得向上运动的速度分量变大,颗粒的径向运动削弱了底部阻力对流速的影响。由图13还可以看出,当浓度不变而流速变大时,速度分布的对称性与速度最大点位置均无明显变化。
4.3 压降
从图14可知,泥浆压降的CFD模拟值和Durand模型计算值的变化趋势均与实测值相吻合,CFD模拟值较Durand模型计算值更接近实测值。对于同一颗粒粒径的泥浆,当流速相同时压降随着浓度变大而增加,且270μm颗粒泥浆较90μm颗粒泥浆压降随浓度变大增加更迅速。当粒径为440μm时,压降的变化趋势与90、270μm的相似(图略)。
此外还可以发现,Durand模型的计算结果均较实测值偏大,其原因是Durand模型的理论基础是重力理论,出发点是使全部颗粒进行悬浮输送,使得模型计算时夸大了泥浆流动的能量损耗,导致模型计算的阻力损失偏大。
5 结论
(1)对于水平管道中的泥浆两相流问题,使用欧拉双流体模型能够很好地模拟管道内的流动状态。颗粒浓度分布、速度分布以及阻力损失的模拟值均与实测值表现出良好的一致性。
(2)在管道垂直中心线上颗粒浓度呈不对称分布,且不对称度随着颗粒浓度增大或泥浆流速变大而降低。粒径较大的粗颗粒在升力作用下,浓度曲线在管道底部近壁面处出现反折。当流速降低或管径增大时,颗粒沉降作用影响更明显,浓度曲线在管道底部的反折现象消失。
(3)颗粒速度分布主要受浓度分布影响,颗粒速度分布在垂直方向上的不对称度随着颗粒浓度增加而变大。当浓度不变而流速变大时,速度分布的对称性与速度最大点所处位置均无明显变化。
(4)在Durand模型的适用范围内,CFD模拟值和Durand模型计算值的变化趋势均与实测值相吻合。CFD模型由于更全面地考虑了相间作用力、更准确地描述了固液两相流的湍流特性,因此其计算结果较Durand模型更接近实测值。

