基于ABCA—SVM的大坝变形预警模型
钱程 李连基 周子东


摘要:合理分析大坝变形监测数据序列特征,精确预测大坝变形状况,是大坝安全监测的重要内容。针对常用大坝安全监测分析模型存在的不足,将人工蜂群算法与支持向量机模型结合起来,利用人工蜂群算法全局搜索能力强、收敛速度快等优点对支持向量机模型的惩罚因子C和核参数6进行优化,建立了ABCA-SVM模型。某水电站大坝坝顶某点的112组径向位移预测实例表明,ABCA-SVM模型预测精度高于标准SVM模型的,可以在大坝安全监测领域推广应用。
关键词:大坝安全;变形监测;人工蜂群算法;支持向量机
中图分类号:TV698.1
文献标志码:A
doi: 10.3969/j.issn.1000-1379.2018.04.030
大坝的变形情况能较客观地反映大坝的运行状况,根据大坝变形实测资料建立大坝安全监测模型对大坝安全稳定运行起着非常重要的作用。近年来随着信号处理技术、人工智能方法的不断涌现和推广,各种智能模型(神经网络模型、支持向量机(SVM)模型、小波网络模型等)相继被提出。其中支持向量机模型对解决一些小样本、高维数、非线性的问题有很好的效果,且具有良好的泛化能力和鲁棒性,在大坝安全监测建模中受到广泛关注。SVM参数的选择直接影响其预测精度和泛化性能。目前对SVM参数进行寻优的方法主要有遗传算法、粒子群算法、模拟退火算法,但由于遗传算法收敛速度较慢,粒子群算法容易陷入局部最优,模拟退火算法的参数难以控制,因此笔者采用人工蜂群算法(ABCA)优化SVM中的参数,以期提高该模型的预测精度。
1 支持向量机基本原理
支持向量机(SVM)以统计学理论为基础,能够有效解决多维函数的预测、分类问题,以及复杂的非线性回归问题,其基本思想是利用内积函数将输入空间的非线性变量映射到一个高维空间,并在高维空间进行线性回归,即式中:6为阈值;w为高维特征空间;Φ(x)为非线性映射。
这样,就将低维空间的非线性问题转化为高维空间的线性问题。因非线性映射是固定不变的,故式中:l、e(·)、λ分别为样本的数目、损失函数、常数(可以调整);xi、yi为一维空间的白变量和因变量。
最小化R(w),可以得到式中:χi和χ*i为最小化R(w)的解。
根据式(1)、式(3),得式中:k(xi,x)=Φ(Xi)·Φ(x),称为核函数(满足MerCer条件的任何对称的核函数对应于特征空间的点积)。
SVM回归模型的关键在于核函数和核函数参数的选取。关于核函数的选择,径向基函数(RBF)是一种常用的核函数,而且效果较好。关于核函数参数的选取,笔者采用人工蜂群算法对惩罚因子C和核参数δ进行迭代寻优,找到合适的参数代人SVM模型,以期提高ABCA-SVM模型的预测精度。
2 人工蜂群算法
2.1 算法原理
人工蜂群算法是一种建立在蜜蜂群体智能白组织模拟模型基础上的群集智能优化算法,该算法由KarabogaD.于2005年提出,最初应用在函数数值优化。该算法将群体分为侦查蜂、观察蜂和采蜜蜂3种,包括为食物源招募蜜蜂和放弃某个食物源两种行为。算法中,每个蜜源的位置(即待求函数的决策变量)代表优化问题的一个可行解,蜜源的质量即对应可行解的质量。
算法程序模拟真实蜜蜂采蜜过程:①初始化生成n组随机解,n为采蜜蜂数即蜜源数,变量x=(xi)(i=l,2,…,d)为一个d维向量(d为优化参数决策变量的个数),同时对这n组解进行评价;②采蜜蜂根据蜜源的局部位置信息产生新的蜜源并进行评价,若新蜜源比初始蜜源好则替代,否则初始蜜源不变化:③根据蜜源的质量,观察蜂通过既定的“优胜劣汰”机制,以较高的概率选取优质蜜源,在选取的同时,根据蜜源处的局部信息产生一组新蜜源,若新蜜源质量优于旧蜜源则将其替代,否则不变。
采蜜蜂和观察蜂在不断循环上述步骤后逐步改善蜜源的质量,获取优质蜜源的位置。但在经历若干次选择后,若某些蜜源位置没有发生改进,则执行侦查蜂操作,放弃该蜜源,寻找一组新蜜源替代并如前述方法一样进行评估。整个过程不断反复执行,记录每步最优解,直至达到既定的循环次数或预定精度。
2.2 数学描述
以最小优化问题为例,食物源的花蜜量对应于实际解的适应度为式中:FITi为某组蜜源对应的质量:fiti为目标函数。
某组蜜源被选中的概率为
采蜜蜂判断蜜源的优劣程度后,领域内产生新解的公式为式中:ψ为(一1,1)的随机数;i∈(1,2,…,d),k∈(1,2,…,d),且k≠i;xij为领域中心;xij-Xhj为领域范围。
偵查蜂放弃某蜜源,产生替补新蜜源的公式为式中:x'max和x'min为i维度的上下界,由此产生的新蜜源可减少一定的盲目性;rand(0,1)为生成0~1的随机数。
3 基于人工蜂群算法的支持向量机模型
ABCA-SVM模型旨在依靠人工蜂群算法全局搜索能力强、收敛速度快的优点,选取支持向量机较优的惩罚因子C和核参数δ,从而提高ABCA-SVM模型的预测精度。具体操作步骤如下。
(1)数据输入。按成因,大坝变形可分为水压分量、温度分量和时效分量三部分,因此输入数据时需输入影响因素数据(水位、温度和时间)以及位移数据。
(2)将支持向量机惩罚因子C和核参数δ作为人工蜂群算法目标函数的决策变量。
(3)根据求解问题设定目标函数。考虑到大坝变形预测精度,可将剩余平方和作为目标函数,假设有m组观察样本,实际位移为yi,ABCA-SVM模型预测值为yi,则目标函数值为
(4)计算个体适应度。由式(5)可知,目标值越小适应度越大,目标值被选择的概率越大。
(5)优化得出新解后,计算新模型的相关统计学指标,并与原模型比较。如此反复,直至结果达到满意精度或循环达到既定的次数。
算法流程见图1。
4 实例分析
某水电站位于澜沧江中游,是澜沧江中下游水电规划“两库八级”中的第二级。电站于2002年1月20日开工,大坝为混凝土双曲拱坝,坝高292m,坝顶高程1254m,电站建成后将形成库容为149.14亿m3的水库,可带来巨大的发电、灌溉、航运等综合效益。以该大坝坝顶某点的112组径向位移(2010-08-08至2013-02-08)为样本,利用ABCA-SVM模型对样本进行拟合和预测,并把拟合和预测结果与标准SVM模型结果对比。其中,样本的前82组数据用来拟合,后30组数据用来检验。
ABCA-SVM模型输入数据有水位、温度、时间和位移。该坝为混凝土双曲拱坝,水压分量与水深H-H0、(H-H0)2、(H-H0)3、(H-H0)4有关,其中H、H0分别为监测日、始测日对应的水头。由于没有温度数据,因此温度分量将多周期的谐波作为因子,取,其中:t为监测日到始监测日的累计天数;t0为建模资料系列第一个测日到始测日的累计天数。时间分量取两个影响因子θ-θ0、Inθ-Inθ0,其中:θ为监测日至始测日的累计天数t除以100;θ为建模资料系列第一个监测日到始测日的累计天数除以100。这样总计有10个影响因子。
初始化人工蜂群算法基本參数:蜂群大小为100,最大循环次数为100,放弃蜜源操作的最大执行次数为50,C取值范围为[0.1,100],6取值范围为[0.01,10]。人工蜂群算法优化后的惩罚因子C和核参数6的最佳取值为57.1和0.52。将最佳惩罚因子C和核参数6代人ABCA-SVM模型,计算得出2010年8月8日至2012年6月26日共82组位移数据的拟合值以及2012年7月5日至2013年2月8日共30组位移数据的预测值。将ABCA-SVM模型的拟合值和预测值与标准SVM模型计算结果进行对比。为方便比较,从拟合数据中截取2011年8月11日至2012年3月11日的25组数据,位移实测值和两种模型的拟合值及拟合值的残差见图2、图3。
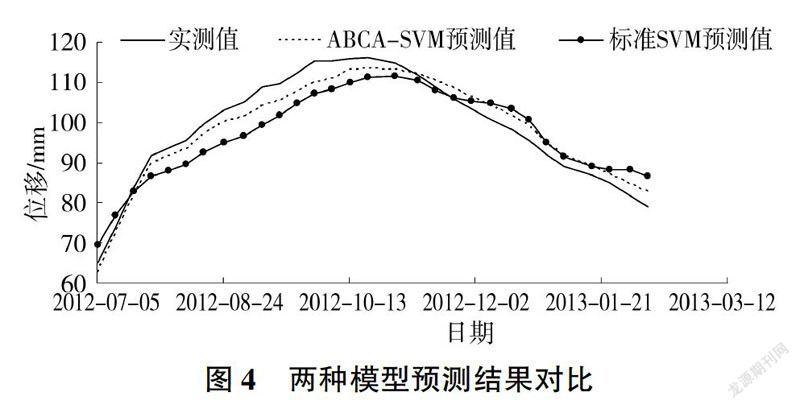
从图2、图3可以看出,标准SVM模型和ABCA-SVM模型均能较好地拟合监测序列,但ABCA-SVM模型拟合值残差明显小于标准SVM模型的拟合值残差,ABCA-SVM模型具有更高的拟合精度。ABCA-SVM模型和标准SVM模型预测值对比见表1、图4。
由表1、图4可知,ABCA-SVM模型预测值的相对误差大多小于标准SVM模型的:两模型进行短期预测时,ABCA-SVM模型的预测结果更接近实测值。综上所述,ABCA-SVM模型在进行小样本数据拟合、预测时精度高于标准SVM模型。
5 结语
将人工蜂群算法与支持向量机结合起来,利用人工蜂群算法全局搜索能力强、收敛速度快等优点对支持向量机的惩罚因子C和核参数δ进行优化,建立了ABCA-SVM模型。实例证明,相比于标准SVM模型,该模型的拟合、预测精度均有一定提高,可以在大坝安全监测领域推广应用。

