黄土区SCS—CN模型径流曲线数计算方法研究
邓景成 高鹏 穆兴民 赵广举 孙文义 田鹏 宋小燕


摘要:美国农业部开发的SCS-CN模型是较为常用的一种径流计算方法。模型中的CN值是模型中反映土地利用、土壤类型和土壤前期含水量的一个综合参数,其值的选择对于准确计算地表径流具有重要意义。利用黄土高原地区杨青川流域、燕沟流域和西川流域不同土地利用类型42场模拟降雨的径流资料,应用平均值法、中值法、算术平均值法、S对数频率分布法和渐近线法5种方法计算CN值,并利用CN值反推径流深。采用均值比较、模型评价指标的方法比较了5种方法计算的径流深与实测值的差异,根据相对隶属度最大最优原则确定最优计算方法。结果表明:在杨青川流域,最优的计算方法是平均值法,燕沟流域和西川流域的最优计算方法则是中值法,不同流域同一计算方法确定的同一土地利用类型CN值差异较大;单独进行草地和裸地的评价分析时,草地的最优计算方法是平均值法,裸地的最优计算方法是算术平均值法,不同土地利用类型CN值的最优计算方法不同。
关键词:相对隶属度;径流深;径流曲线数;SCS-CN模型;黄土区
中图分类号:TV121; P333
文献标志码:A
doi: 10.3969/j.issn.1000-1379.2018.04.003
径流计算是区域径流量预测及水资源评价模型的重要组成部分,常采用Green-Ampt人渗曲线、Philip人渗曲线以及Horton人渗曲线等方法进行计算,但这些方法所需参数较多且不易获取,难以实际应用。SCS-CN模型4-9-是美国农业部研制的用于计算给定降雨条件下一定区域地表径流的经验模型,因其结构简单,仅需一个反映土壤类型、土地利用覆被状况以及前期土壤湿度的参数——径流曲线数(CN)即可计算已知降雨条件下的地表径流量,故被广泛应用于许多国家的流域水文模型中,应用效果也较好。CN值是一个无量纲参数,由前期土壤湿度(AMC)、土壤类型、土地利用、坡度等因素决定,W.C.Boughton的研究表明,CN值变化±10%就会引起径流量计算结果分别变化+55%、-45%。因此,CN取值对于准确计算区域地表径流量具有重要意义。
SCS-CN模型的CN值是美国农业部根据土壤水文条件、土地利用方式确定的,并列有对应的CN查值表。我国应用时一般根据土地利用类型以及前期土壤湿度由查值表得到CN值。由于美国的植被状况、土壤类型、产流机制与我国存在差异,因此在应用SCS-CN模型时要根据研究区的实际情况对CN值进行修正。对于具有一定年限观测资料的地区,可采用反推的方法计算研究区的CN值,因此选择合适的方法反推CN值才能更准确地计算地表径流量。目前,CN值的反推方法主要有平均值法、中值法、算术平均值法、S对数频率分布法和渐近线法5种。符素华等以北京密云石匣径流小区71场实测降雨资料反推CN值,并比较了这5种方法的精度,结果表明在北方土石山区CN值的5种计算方法精度各异,从模型有效系数看,渐近线法的计算结果最好:从相关系数和合格率来看,算术平均值法的计算结果最好。然而,关于黄土区CN值的计算方法研究较少,以往研究主要集中在比较不同土地利用类型或植被下的CN值以及CN值随坡度的变化等,对于黄土区CN值计算方法的适宜性研究较少。本文以黄土区不同流域42场野外人工模拟降雨试验资料反推CN值,以比较这5种方法在黄土区不同土地利用类型下的计算精度,以期为黄土区由实测降雨资料反推CN值提供参考和指导建议。
1 CN值的基本计算
SCS-CN模型是基于水分平衡方程和兩个基本假设提出的经验模型,其CN值是一个反映土地利用、土壤类型、水文条件和前期土壤湿度的综合性指标,取值范围为0~100。土壤类型分为A、B、C、D4类,由土壤最小下渗率和土壤质地确定,人渗能力依次减弱。前期土壤湿度由前期降水指数(API)确定。运用降雨量与径流量反推CN值的公式为
S=5(P+2Q-√4Q2+5PQ)
(1)
CN:25400/254+S
(2)式中:S为流域最大人渗量;P为流域内总降水量;Q为流域内实际径流量。
2 研究方法
2.1 研究区概况
研究区选取延安市南部的燕沟流域、吴起县南部的杨青川流域和安塞县南部的西川流域,各流域概况见表1。
2.2 降雨试验概况
由于模拟降雨装置受风的影响较大,因此选择在清晨无风的5:00-6:00进行试验,以减轻风对试验结果的影响。每次人T降雨前,对试验小区表层0~100cm土壤各层(每IOCm-层)含水量采用烘干法进行测定,以监测每次试验的土壤前期含水量。降雨试验在每个小区轮流进行,试验期间尽量减少对小区的人为扰动,裸地小区采取翻晒、整平处理。试验前在小区对角线上布置3个翻斗式自计雨量筒,记录每次试验的降雨量。降雨时,记录小区产流时间,定时用塑料桶采集径流泥沙样品,时间间隔为1min。杨青川流域内的试验采用两侧对喷式降雨装置模拟降雨,喷头高约6m,共设草地和裸地两种小区(两种类型分别设12.0°、25.0°两个坡度),小区尺寸为5mx2m(长度×宽度),草地产流时间为降雨开始后131~359s,裸地产流时间为降雨开始后73~191s:燕沟流域采用折射式单向喷射喷头降雨装置,雨滴降落高度>15m,共设草地(坡度为26.50)和裸地(坡度为25.80)两种小区,小区尺寸为5mxlm(长度×宽度),草地产流时间为降雨开始后97~152s,裸地产流时间为降雨开始后93~257s:西川流域采用下喷式降雨装置,雨滴降落高度为6m,共设草地(坡度为13.00)和裸地(坡度为20.00)两类小区,小区尺寸为4mxlm(长度×宽度),草地产流时间为降雨开始后125~257s,裸地产流时间为降雨开始后103~184s。侧喷式装置通过更换喷头出水孔的孔径来调整降雨强度,下喷式则通过电脑直接设置降雨强度。降雨试验信息及场次见表2。
美国农业部水土保持局考虑AMC对径流的影响,引入前期降水指数API(Antecedent PrecipitationIndex)确定前期土壤湿度,分为AMC I(干旱)、AMCⅡ(正常)和AMCⅢ(湿润)三种等级,分别对应CN1、CN2、CN3。划分依据见表3。
试验时间安排在2015年8月19日-9月26日和2016年8月5日-9月1日,属于生长期。用烘干法测定的土壤含水量:0~50cm平均为20.45%+0.13%:0~100Cm平均为17.18%+0.14%。降雨试验安排在湿度较高的清晨,再加上小区的前期降雨,确定土壤前期湿度等级为AMCⅢ级,试验计算得到的CN值均为CN3。
2.3 数据处理
2.3.1 CN值计算方法
(1)平均值法。依据降雨径流资料按式(1)计算出每组数据的s值,再求出s的平均值,代人式(2)得到CN值。
(2)中值法。按式(1)计算出每组数据的S值,将S从小到大排序,取居于中间的数(若该组数据个数为偶数,则取位于中间的两个数的平均值)作为中值,代人式(2)得到CN值。
(3)算术平均值法。按式(1)计算出每组数据的S值,再求出每一个S值对应的CN值,取所得CN值的平均值为最终结果。
(4)S对数频率分布法。具体步骤:①根据降雨径流资料计算相应的s值:②对s值取对数,并按递减方式排序,求s值的对数经验频率分布曲线:③根据s值的对数经验频率分布曲线,求出频率为50%时的S值:④根据式(2)求出相应的CN值,此值作为土壤水分状况为一般时的CN值:⑤以相同的方法分别求出频率为10%、90%时的s值及相应的CN值,作为土壤水分状况为干燥、湿润时的CN值。
(5)渐近线法。具体步骤:①将降雨量和径流量分别按大小排序,将同一序数下的降雨量和径流量组成新的数据对,此时同一重现期下的降雨量有对应重现期的径流量:②利用新的降雨量和径流深数据对,根据式(1)、式(2)计算相应的s值和CN值;③将计算出的CN值与相应的降雨量组成数据对,点绘降雨量与CN的散点图,并根据散点图配线,可得到CN值和降雨量的关系曲线,以渐近线值作为CN值。
2.3.2 评价参数选取
为了筛选最合适的计算方法,选用的评价指标有平均误差(ME)、均方根误差(RMSE)、相关系数(CC)、相对误差(Bias)和纳什系数(NSE)。ME和RMSE用来衡量实测值与模拟值的误差,CC衡量实测值与模拟值的相关性程度,Bias与NSE评价实测值与模拟值的拟合程度。ME、RMSE和Bias均为越小(绝对值)越优型指标,CC和NSE为越大越优型指标。
3.3 模糊优选模型
设由n个待优选方案组成系统的优选方案集,又m个因素(或评价指标)组成对优选对象进行评判的系统因素集,则可得方案的因素特征值矩阵X:式中:xij为方案j中指标i的特征值,i=1,2,…,m;j=1,2,…,n。
由于各指标特征值的量纲不同,因此需要进行规格化。越大越优型和越小越优型指标特征值的规格化公式为式中:rij为方案j中指标i的相对隶属度。
经过规格化处理,指标特征值矩阵X即可变换为相对隶属度矩阵R=(rij)。
设m个指标的权重向量为W=(W1,W2,…,wm)T,且满足,则方案j的相对隶属度为uJ可表示为式中:p为可变距离参数,本文取p=2。
式(5)即为模糊优选模型,最终求得n个方案的相对隶属度U=(U1,U2,…,Un),根据最大隶属度原则即可选出较优的方案。
2.3.4 模拟径流值计算及比较
通过上述5种方法计算得到杨青川流域、燕沟流域和西川流域不同土地利用类型的CN值以及所有场次降雨情況下按土地利用类型分类的CN值。为了比较同一条件下5种计算方法的优劣,选用初损率λ为标准值0.2来计算模拟径流深,并分别计算模拟径流
3.1.2 由CN值反推的径流深与实测值的比较
由表5可看出:杨青川流域平均值法得到的径流深模拟值与实测值最为接近,S对数频率分布法偏差最大(偏大16.05%);燕沟流域中值法得到的径流深模拟值与实测值最为接近,S对数频率分布法偏差最大(偏大14.61%);西川流域也是中值法计算结果与实测值最相近,S对数频率分布法偏差最大(偏大36.04%)。与S对数频率分布法和渐近线法相比,平均值法、中值法和算术平均值法得到的径流深模拟值与实测值相比偏差都较小,误差为0.02~1.13mm。
3.1.3 模拟径流深与实测径流深误差分析
从表6可以看出:在杨青川流域,平均值法得到的模拟径流深的ME、RMSE和Bias指标绝对值最小(分别为-0.0246、2.5436、-0.0014),平均值法的NSE指标最大(为0.9575),S对数频率分布法的CC值最大(为0.9791):在燕沟流域,中值法计算的模拟径流深的ME和Bias最小(分别为0.0510、0.0033),平均值法的RMSE最小(为2.9708),平均值法的CC和NSE深的均值、各评价指标及相对隶属度。
3 结果与分析
3.1 不同流域相同土地利用类型的计算结果比较
3.1.1 不同区域各方法计算的CN值
按照平均值法、中值法、算术平均值法、S对数频率分布法和渐近线法5种方法计算得到的不同地区各土地利用类型CN值见表4。从表4可以看出,不同计算方法得到的CN值存在显著差异。杨青川流域草地和裸地各计算方法中渐近线法结果均最小,分别为73.15、88.96,S对数频率分布法结果均最大,分别为82.52、92.08:燕沟流域草地用平均值法结果最小,裸地则是渐近线法结果最小,分别为66.19、86.02,s对数频率分布法计算结果均最大,分别为69.53、88.92;西川流域两种土地利用类型用渐近线法结果均最小,分别为64.47、73.97,s对数频率分布法结果均最大,分别为73.88、82.37。其中对于同一流域平均值法、中值法和算术平均值法计算的CN值相差较小,相差0.04~0.67。最大(为0.9289、0.7694):在西川流域,算术平均值法计算得到的模拟径流深的RMSE最小(为6.6572),平均值法的CC最大(为0.8777),中值法的ME和Bias绝对值最小(分别为0.3495、0.0216),算术平均值法的NSE最大(为0.7496)。
综合各评价指标看,平均值法和中值法用于计算模拟径流深时误差较小,模拟径流深与实测值的相关性较好,拟合程度也较好。S对数频率分布法和渐近线法的相关系数和纳什系数较高,但误差较大,对于径流预测影响较大。
3.1.4 由相对隶属度筛选最优计算方法
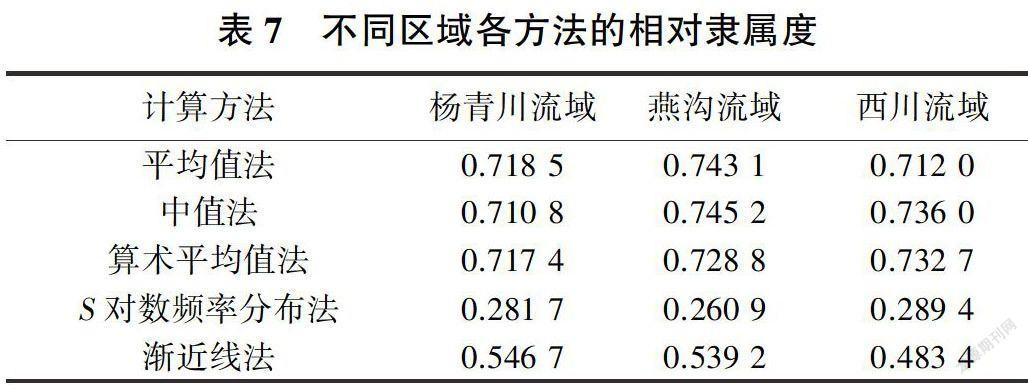
上述各评价指标的计算方法并不唯一,不能直观反映哪种方法最优。由于人们对各个指标的关注程度不同,因此选用模糊优选模型进行筛选。RMSE、CC分别反映预测值与实测值的离散程度和相关程度,NSE反映预测值与实测值的拟合程度,应给予较高的权重,因此将5个指标的权重向量定为W=(0.15,0.20,0.20,0.15,0.30)T,计算的相对隶属度见表7,根据相对隶属度最大原则选定最优计算方法。由表7可以看出,杨青川流域的最优计算方法为平均值法,燕沟流域和西川流域的最优计算方法均为中值法。不同区域有不同的最优计算方法,与计算复杂的s对数频率分布法和渐近线法相比,计算简单的平均值法、中值法和算术平均值法计算的径流深在误差及拟合程度上效果更好。
3.2 草地和裸地CN值计算方法的比较
对3个地区所有草地和裸地的降雨资料进行整理,计算各评价指标,用相对隶属度最大最优原则确定最优计算方法。
3.2.1 草地和裸地的CN值
由表8可以看出:草地和裸地的CⅣ值差异显著,仍然是平均值法、中值法和算术平均值法计算的CN值较为接近,S对数频率分布法和渐近线法差异较大:草地的模拟径流深都偏大,平均值法模拟值与实测值最为接近,偏大0.45mm,S对数频率分布法则偏大9.27mm;裸地则算术平均值法误差最小,偏小0.40mm,S对数频率分布法偏大9.26mm。
3.2.2 误差与相对隶属度计算
分别计算5种方法模拟得到的径流深各评价指标(见表9),可以看出平均值法、中值法和算术平均值法用于模拟草地和裸地径流深的误差都较小,拟合程度也较好,且草地的NSE为负值。排除NSE的影响,选用其余4个指标进行计算,根据指标重要性确定权重向量W=(0.2,0.3,0.3,0.2)T,相对隶属度的计算结果见表10。根据相对隶属度最大最优原则可得出,草地用平均值法计算的CN值模拟得到的径流深结果最优,而裸地则是算术平均值法为最优计算方法。由于不同流域草地和裸地径流深的模拟值与实测值的NSE差异较大,表明不同区域用5种计算方法确定的CN值反算径流深时误差较大,因此同一个区域运用5种计算方法确定的CN值只适合本区域的模拟预测。
4 结论
(1)对比5种计算方法,平均值法模拟得到的径流深与实测值比较,RMSE最小,CC最大,且拟合程度最好:就ME和Bias来看,中值法模拟的径流深与实测值更接近。根据相对隶属度最大最優原则,确定杨青川流域CN值的最优计算方法是平均值法,燕沟流域和西川流域的最优计算方法则是中值法。
(2)比较所有降雨资料中的草地和裸地,表明用平均值法计算草地的CN值,进而模拟径流深的ME、RMSE和Bias最小:裸地则是算术平均值法计算得到的ME、RMSE和Bias最小。根据相对隶属度最大最优原则确定草地CN值的最优计算方法为平均值法,裸地的最优计算方法是算术平均值法。
(3)不同流域同一计算方法确定的同一土地利用类型的CN值差异较大,且不同流域计算CN值的最优方法也不同。整合同一土地利用类型的降雨资料计算分析,模拟结果的NSE较低,拟合程度较差。由于不同流域降雨试验时野外试验条件存在差异,因此其降雨强度、降雨历时等试验控制参数不一致,可能影响了研究结果。对于气候、植被和地形差异对CN值的影响,应进一步控制试验其他参数进行论证。

