跌坎型消能工冲击区流速衰减规律研究

崔召 王海军 刘家伟

摘要：跌坎型底流消能工冲击区对消力池的消能效率具有决定性的影响，而冲击区入射主流轴线流速沿程衰减规律及机理尚不明确。采用水工模型试验方法，开展了冲击区主流轴线最大流速与跌坎深度、入池流量之间相互关系的研究，结果表明，跌坎型底流消能工冲击区入射主流轴线流速的衰减遵循一般的射流衰减规律。通过水工模型试验结果的无量纲化，给出了u（i）max/u₀（入射主流轴线各特征断面点流速的无量纲值）- x_i/L（入射主流轴线各特征断面点距离的无量纲值）的关系，研究结果表明：跌坎型底流消能工冲击区入射主流轴线流速衰减规律不受跌坎深度、入池流量的影响，具有相似的衰减趋势；入射主流轴线流速沿程衰减拟合曲线表明入射主流轴线流速沿程得到充分衰减。

关键词：跌坎型底流消能工；水工模型试验：冲击区；流速衰减规律；无量纲化；水力学指标

中图分类号：TV135.2

文献标志码：A

doi： 10.3969/j.issn.1000-1379.2018.06.027

底流消能作为主要的泄洪消能方式之一，具有流态稳定、消能效果好、对尾水水位变化适应性强、泄洪雾化轻微等优势[1]。跌坎型底流消能工[2]是在常规底流消能型式基础上发展而来的一种新型消能工，其体型为在消力池进口处，将消力池底板整体向下开挖，构成纵剖面上有一定垂直深度的跌坎型消力池[3]。跌坎型底流消能工消力池内的高速水流沿程得到扩散[4]，使得能量得以消散，进而达到降低临底流速、保护消力池底板的目的[5]。

跌坎型底流消能工内，淹没射流主流到达消力池底板并与底板相互作用的区域称为冲击区[6]。在冲击区，淹没射流主流冲击消力池底板，受到底板的约束[7]，临底区域流向发生改变[8]，入射主流的部分动能转化为底板上的压能[9]，大部分动能得到消散，使得主流流速迅速降低。冲击区是消力池内主要的消能区域[1O]，其水力特性对消力池的消能效率具有决定性的作用。

跌坎型底流消能工在入射主流进入消力池后，沿主流方向的流速随射程的增加而减小。但是，目前研究成果[11-13]只针对入射主流的沿程衰减规律，而很少涉及对其的定量描述。基于这种情况，本文从水T模型试验出发，着重对跌坎型底流消能工冲击区入射主流轴线流速沿程衰减规律与机理进行试验研究。

1 试验模型

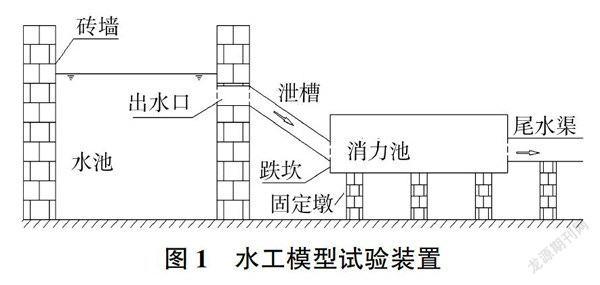
选定3个跌坎深度（d=6、8、10 cm）、3个水流入池角度（θ= 15°、30°、45°）以及3个人池流量（Q1= 6.13x10^-3、Q2= 8.03 x10^-3、Q3=10.32×10^-3m3/s）为试验工况，试验装置如图1所示。通过对跌坎型底流消能工消力池内水流流态的观测，分析消力池内水流结构[14]，如图2所示。通过实测冲击区入射主流轴线各特征断面点的流速，分析消力池内冲击区流场结构[15]，并着重分析跌坎型底流消能工冲击区人射主流轴线流速沿程衰減规律与机理。

2 试验结果分析

2.1 冲击区主流轴线最大时均流速衰减机理

试验选择跌坎型底流消能工消力池冲击区入射主流轴线断面作为研究对象，研究冲击区入射主流轴线流速沿程分布与衰减情况。以泄槽末端入射断面的人池流速₀为基准，对入射主流轴线各特征断面的最大时均流速u（i）max进行无量纲化处理，得到主流轴线流速无量纲值u（i）max/u₀）与主流轴线各特征断面到入射断面的距离x_i之间的关系曲线。水力学指标参数之间关系示意见图3，水力学指标参数见表l。

人池流量一定（以Q3= 10.32xl0^-3m3/s为例），不同人池角度[16]对应的实测最大时均流速见表2，u（i）max/u₀与x_i之间的关系见图4。

由图4可知：①u（i）max/u₀）与x_i）成反比关系，即随着入射主流轴线各特征断面到入射断面之间距离的增大，主流轴线流速无量纲值逐渐减小：②人池流量一定、跌坎深度相同时，人池角度增大使得入射主流轴线流速沿程总衰减率减小。

为进一步研究跌坎深度变化对冲击区入射主流轴线流速沿程衰减规律的影响[17]，分析人池流量一定（以Q3= 10.32xl0 -3 m3/s为例）时，各人池角度下不同跌坎深度对应的u（i）max/u₀）与x_i之间的关系（见图5）。

由图5可知，在不同跌坎深度工况下，主流轴线流速的沿程衰减曲线具有相似的趋势。

跌坎深度一定（以d=8 cm为例）时，各人池流量下不同人池角度对应的实测最大时均流速见表3，Q3= 10.32xl0 -3 m3/s、d=8 cm时对应的最大时均流速见表2，u（i）max/u₀与x_i的关系见图6（Q3=10.32×l0 -3m3/s、d=8 cm时对应的曲线见图4（b））。

由图6、图4（b）可知：①主流轴线流速无量纲值u（i）max/u₀与主流轴线各特征断面到入射断面距离x_i成反比关系，即随着人射主流轴线各特征断面到入射断面之间距离的增大，主流轴线流速无量纲值逐渐减小：②在跌坎深度一定、人池流量相同的工况下，人池角度的增大使得入射主流轴线流速的沿程总衰减率减小。

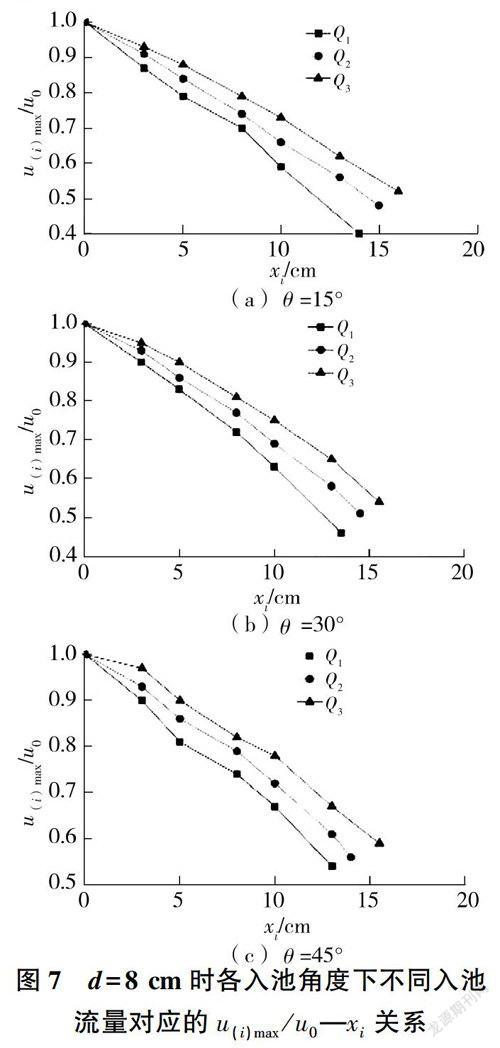
为进一步研究人池流量变化对冲击区入射主流轴线流速沿程衰减规律的影响，分析跌坎深度一定（以d=8Cm为例）时，各人池角度下不同人池流量对应的u（i）max/u₀与x_i之间的关系（见图7）。

由图7可知：①在不同人池流量工况下，主流轴线流速的沿程衰减曲线具有相似的衰减趋势：②随着人池流量的增大，冲击区入射主流轴线流速的沿程总衰减程度有所降低，即冲击区入射主流轴线流速沿程总衰减率减小。

因此，在人池流量和跌坎深度一定的工况下[18]，冲击区主流轴线流速无量纲值u（i）max/u₀。与主流轴线各特征断面到入射断面距离x_i成反比关系，即随着主流轴线各特征断面到入射断面之间距离的增大，主流轴线流速无量纲值逐渐减小：同时，在人池流量一定的工况下，随着跌坎深度的改变，冲击区入射主流轴线流速的沿程衰减曲线具有相似的衰减趋势：在跌坎深度一定的工况下，随着人池流量的改变，冲击区入射主流轴线流速的沿程衰减曲线亦具有相似的衰减趋势。从而可知，跌坎型底流消能工冲击区入射主流轴线流速的沿程衰减遵循一般的射流衰减规律，即在自由紊动射流沿程扩展的过程中，其纵向时均速度是沿程衰变的[19]。但是，在跌坎深度和人池流量相同的工况下，人池角度的增大使得入射主流轴线流速的沿程总衰减率减小，即消力池消能率的提高不能一味地追求人池角度的增大。

2.2 冲击区主流流速衰减机理

為进一步分析跌坎型底流消能工冲击区入射主流轴线流速沿程衰减规律，以泄槽末端断面人池流速u₀为基准，对入射主流轴线各特征断面的u（i）max进行无量纲化处理：以消力池冲击区入射主流轴线长度为基准，对主流轴线各特征断面到入射断面距离x_i进行无量纲化处理。从而得到相同人池角度、不同跌坎深度工况下（u（i）max/u₀）-（x_i/L）的关系曲线（L为消力池冲击区入射主流轴线长度）。

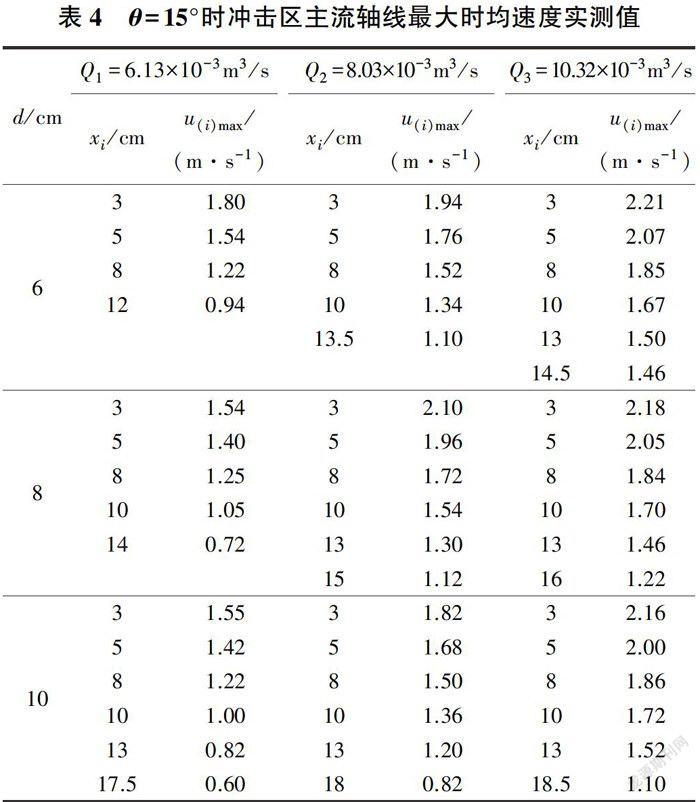
人池角度为15°时，不同人池流量[20]对应的实测最大时均流速见表4，（u（i）max/u₀）-（x_i/L）关系见图8。

由图8可知：①当人池角度为150时，在不同跌坎深度工况下，冲击区入射主流轴线流速沿程分布具有相似的衰减趋势，拟合线均为斜率为负值的直线，并且拟合曲线的斜率随着跌坎深度的增大而增大：②跌坎深度较大时冲击区入射主流轴线流速沿程总衰减率大于跌坎深度较小时的沿程总衰减率。

人池角度为300时，不同人池流量对应的（u（i）max/u₀）-（x_i/L）关系见图9。

由图9可知：①当人池角度为300时，在不同跌坎深度工况下，冲击区入射主流轴线流速沿程分布与人池角度为15°时衰减趋势相似，拟合线的斜率随着跌坎深度的增大而增大：②跌坎深度较大时冲击区入射主流轴线流速沿程总衰减率大于跌坎深度较小时沿程总衰减率。原因是随着跌坎深度的增大，冲击区入射主流轴线长度增长，入射主流得到充分发展，使得冲击区入射主流轴线流速沿程得到充分衰减。

人池角度为45°时，不同人池流量对应的u（i）max/u₀）-（x_i/L））关系见图10。

由图10可知：①当人池角度为450时，在不同跌坎深度的工况下，冲击区入射主流轴线流速沿程分布与人池角度为15°、30°时衰减趋势相似，拟合曲线的斜率随着跌坎深度的增大而增大：②随着跌坎深度的增大，冲击区入射主流轴线流速沿程总衰减率有所增大：③当跌坎深度为6、8 cm时，冲击区入射主流轴线流速沿程衰减趋势近乎相同：当跌坎深度为10 cm时，各特征值分布较分散，说明冲击区人射主流轴线流速沿程得到充分衰减，主流轴线流速沿程总衰减率较高。

3 结论

（1）在人池流量和跌坎深度一定的工况下，冲击区入射主流轴线流速无量纲值u（i）max/u₀与主流轴线各特征断面到入射断面距离xsub>i