基于随机森林算法的吴堡站测流断面形态预测
刘炜 赵丽霞 赵淑饶 赵晶


摘 要:在水文站洪水期流量测验中,受风浪和漂浮物的影响以及设施设备的限制,断面测量是一直以来的难点。传统的断面邻近借用法在断面发生较大冲淤变化时会造成较大的流量计算误差。根据水深与流速之间存在的相关性,使用随机森林算法,以流速分布、水位、河宽等作为输入参数建立断面形态预测模型,对吴堡站测流断面形态进行了预测。结果表明:使用基于随机森林算法的断面形态预测模型来确定测流断面形态是对传统的断面邻近借用法的有力补充:吴堡站流量在3 000 m3/s以上测次的流量预测标准差为13%,大于规范标准,模型仍需改进。建议从两方面来提高断面形态预测的准确性:一是增加特征垂线实测水深等附加参数:二是从断面变化角度出发分析断面冲淤与水沙过程的关系,进而找到更多的影响因子加入回归模型。
关键词:随机森林算法:形态预测:测流断面:吴堡站
中图分类号:P333:TV882.1
文献标志码:A
doi: 10.3969/j.issn.1000-1379.2018.06.003
流量是反映江河湖库水量变化的基本资料。实测流量时,应根据测流设施设备实际情况,在保证测验精度的前提下,因地制宜地采用合适的测流方法。对于水文测站,当遇大洪水或急涨急落的小洪水时,由于洪水来势凶猛,漂浮物较多,因此全面实测水深、流速的难度较大,此时可以依据有关规范采用水面流速法测流,其形式包括传统的浮标法测流[1]以及近年来出现的微波流速仪、雷达枪等非接触手段。对于水面流速,高洪期间的过流断面测速传统上采用借用方法,即按照“峰前借峰前,峰后借峰后,邻近借用”的原则进行估算。借用断面的形态是否合理是影响高洪流量测验精度的关键因素。提高断面形态的预测精度,能有效提高洪水过程的测验质量和报汛精度。
近年来,人T神经网络[2-3]、小波神经网络模型[4-5]和支持向量机[6-7]等机器学习算法被广泛应用于水文预报中。河宽、水深、流速等因素相互作用,共同影响了测验断面的基本形态,且水深、流速的相关性较高,本文以吴堡水文站为例,采用随机森林算法构建了断面形态预测模型。
1 随机森林断面形态预测模型
1.1 随机森林算法
随机森林算法[5]是机器学习算法的一种,其适应性较强,可用于解决非线性回归问题。决策树是随机森林算法的基础分类器,其构造由一个独立同分布的随机向量决定。如果将决策树看成分类任务中的一个专家,那么随机森林算法是许多专家在一起对某种任务进行分类。随机森林算法是由多个决策树组成的分类器,输入向量的最终所属类别由算法中所有的决策树投票决定。决策树通过对参数数值(白变量)进行不断划分来确定因变量数值,从而建立自变量一因变量映射关系。在每“棵”决策树的构造过程中,其分支处参数的选择和划分都是随机的,因此得到的因变量数值也具有一定随机性。在随机森林算法中,当决策树数目很大时遵循大数定律,随机森林算法不会随着分类树的增加出现过度拟合,但有一个有限的泛化误差值。
随机森林算法应用广泛,在水文气象方面,也有基于随机森林算法的暴雨洪水预报等模型。本文是随机森林算法应用于洪水期流量测验断面预测的一次初步尝试。
1.2 模型构建和参数选择
本文使用scikit -learn算法集合中的Random Forest类建立断面形态预测模型,依据随机森林算法在解决非线性问题及其在决策树构建和综合过程中对数据特征识别方面的优势,将其作为模型的核心算法。模型总体上包括数据集划分、模型训练、模型测试和检验指标计算等组成部分,见图1。
模型训练是指将训练集合中的选定参数作为自变量、目标函数的实测值(垂线水深)作为因变量输入模型并建立断面形态预测模型的过程。本文根据随机互斥原则,将数据集按照85:15的比例划分为训练集和测试集。在模型测试阶段,将测试集中的选定参数输入模型,模型输出目标函数预测值。模型检验针对测试集目标函数的实测值及其预测值进行,具体而言就是以实测水深来检验预测水深的准确度。采用均方误差(MSE)和决定系数(R2)两个经典检验指标进行准确度判断:式中:yi为水深预测值;yi为水深实测值;y为平均水深。
在断面形态预测模型中,预测因子是白变量,断面形态是因变量。模型预测因子的挑选采用逐步筛选法,对于所有的检验样本,随机打乱某一白变量取值,再用模型对样本进行测试,拟合误差越大,说明该解释变量越重要。随机森林模型通过R代码( RF.impor-tances)給出了每个白变量对因变量作用的重要性的计算命令,计算得出的各自变量重要性之和为1,计算值越大表示该变量越重要,在解释变量重要性的基础上,采用随机森林算法的回归功能进行断面形态预测。
2 实例应用
2.1 吴堡水文站概况
吴堡水文站于1935年建站,是国家重要水文站、黄河重点报汛站、大河干流控制站,位于陕西省吴堡县宋家川镇柏树坪村,距河口站距离为1544 km,集水面积为433 514 km2。吴堡站测验河段基本顺直,河势稳定,主流偏有。流向与断面基本垂直。基上(基准断面上游)2 300 m有急弯,基下230 m右岸有一小支沟,流域面积约为30 km2,最大山洪流量为200 m3/s。主槽较稳定,主流一般在起点距320 m左有,大水时略向有岸移动。下游小支沟涨水时,若黄河干流流量小于1 000 m3/s,则对水面比降有一定影响,大于1000 m3/s时没有影响。
本文选取吴堡站1953-2012年流量大于1 000m3/s的1 237次实测断面流量测次(垂线20 855条)作为数据全集,使用全集中的85%(1 051个测次,垂线17 700条)作为训练集,用于模拟训练,构造随机森林模型:其他15%(186个测次,垂线3 155条)作为测试集,用来对模型进行检验和评估。训练集和测试集采用随机分配的方法进行划分。
2.2 断面形态预测因子的选取
断面形态预测模型的回归目标是由垂线水深构成的断面形态。断面形态与水沙量级有关,水位可以作为其代表,由于断面形态与流速分布存在相关性,因此选择水位、垂线起点距、垂线平均流速作为首选参数。又因为断面形态预测中影响这3个参数的因子有很多,所以从流速分布(起点距一流速数组)中提取左岸水边起点距、右岸水边起点距、垂线最大流速3个特征值作为模型的待选参数,其中前两个值代表了断面横向的位置和河宽,后一个值兼顾表征水沙量级和流速极值特征。
模型预测因子挑选采用逐步筛选法。本文以不同起点距位置的垂线平均流速作为初选预测因子,将对应起点距位置的测次垂线水深作为预测对象,输入逐步筛选程序,并设置F检验的显著性水平α= 0.1,以垂线流速分布、水位、垂线最大流速、过水断面起点距范围等为参数,采用随机森林算法建立回归模型,预测各起点距对应的水深,根据均方误差和决定系数判断回归性能,筛选出合适的参数组合。不同参数组合的检验结果见表1。
由表1可知,参数组合编号为119的均方差最小(0.29),决定系数最大(0.88),所以最终确定模型的6个参数为水位、左岸水边起点距、右岸水边起点距、垂线最大流速、起点距、垂线平均流速,其中各参数的敏感度见图2,可知垂线平均流速在所有参数中最敏感,其余依次分别为水位、起点距、右岸水边起点距、左岸水边起点距和垂线最大流速。
2.3 预测结果及误差分析
预测断面形态的目的是进行流量计算,因而本文中断面形态预测模型的检验评估分为断面形态、流量两个方面。
2.3.1 断面形态
图3为2012年9月13日9:00断面形态预测结果。以断面面积相对误差作为衡量指标,其概率分布见图4(E80、E60分别为80%、60%概率所对应的最大相对误差的绝对值,loc为误差的平均值.std为标准差),由图4可知回归的断面面积存在1%的系统偏差,相对标准差为14%,检验测次中80%的面积误差小于16%,60%的面积误差小于10%。
2.3.2 流量
流量误差检验方面仍以相对标准差作为主要的评估指标,结果见表2。图5、图6分别为在测试集全集、流量大于3 000 m3/s的测次集合上使用模型进行断面形态回归所计算流量结果的相对误差概率分布。
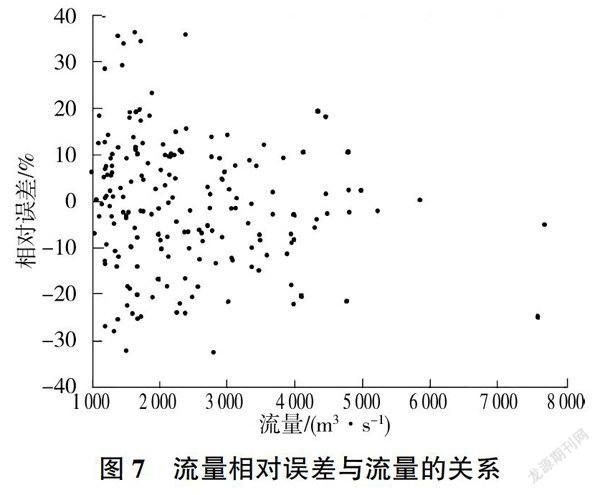
由图6可知流量大于3 000m3/s时相对误差绝对值大都在10%以内,由图7可知相对误差有随着流量增大而减小的趋势,这说明模型对高洪条件有较好的适应性。
从模型在测试集上的回归结果中随机抽取10个3 000 m3/s以上流量测次,预测断面面积与实测断面面积、预测流量与整编流量的比较见表3。
3 结语
(1)采用数学模型来确定测流断面形态是对传统的邻近借用法的有力补充。得益于机器学习算法对历史资料中数据特征的经验性识别,模型预测的断面形态比简单的邻近借用法更有依据。
(2)对吴堡站流量在3 000 m3/s以上测次的断面预测结果表明,流量计算的标准差为13%,大于流量测验规范中浮标法测流标准差小于10%的标准。因此,从生产应用角度出发,该模型仍需改进。
(3)断面形态是水沙过程与河床相互作用的结果。根据目前有限的扩展研究,笔者认为断面形态预测的改进途径有两种:一是增加特征垂线实测水深等附加参数:二是从断面变化角度出发,分析断面冲淤与水沙过程的关系,进而找到更多的影响因子加入回归模型。
参考文献:
[1]郑建民,杨祯祥,郑飞.洪水期浮标法测流应用研究[J].东北水利水电,2016,22(2):33-34.
[2] 袁曾任.人T神经元网络及其应用[M].北京:清华大学出版社.1999:26-41.
[3] KHOTANZAD A, ELRAGAL H, LU T L.Combination ofArtifal Neural Network Forecasters for Prediction of NaturalGas Consumption[J].IEEE, Transactions on Natural Net-work, 2000, 11(2): 464-473.
[4] 陳哲,冯天瑾.小波神经网络研究进展及展望[J].青岛海洋大学学报(白然科学版),1999,29(4):663-668.
[5] 赵学智,邹春华,陈统坚,等.小波神经网络的参数初始化研究[J].华南理工丈学学报(白然科学版),2003,31
(2):77-79.
[6] 李国正,王猛.支持向量机导论[M].北京:电子工业出版社,2005:33-48.
[7] 李红莲,王春花,袁保宗.一种改进的支持向量机NN-SVM[J].计算机学报,2003,26(8):1叭5-1叭9.
[8]
BREIMAN L Random Fore.sts[J]. Machine Learning, 2001, 45(1):5-32.

