基于蒙特卡罗法的感潮河段漫堤风险率研究

李江林 顾圣平 邵雪杰 归力佳 成京

摘要：感潮河段是河流与海洋的过渡段，河道水位受上游径流和河口潮位共同影响。为给河道及堤岸整治提供科學的决策依据，考虑引发漫堤的洪水、潮位、风浪和河道特性等因素，运用蒙特卡罗法结合水力计算，建立感潮河段漫堤风险率计算模型，并以我国沿海某河流感潮河段堤防为例进行实例研究。结果表明：考虑潮位不确定性，漫堤风险率有所提高，堤段越靠近入海口，漫堤风险受潮位影响越明显，适当加高堤防可有效降低感潮河段漫堤风险。

关键词：感潮河段：漫堤风险率：蒙特卡罗法

中图分类号：TV122； P333

文献标志码：A

doi： 10.3969/j.issn.1000-1379.2018.06.叭3

感潮河段洪水期间其水位受洪水及河口潮位双重影响。暴雨导致的上游洪峰与河口高潮相遇，易形成较高洪水位，引发漫堤风险。开展对感潮河段漫堤风险率的研究，可为河道及堤岸整治提供科学的决策依据。现有漫堤风险率分析方法包括直接积分法、极限状态法（JC法）、随机微方程法及蒙特卡罗法（MC法）[1]。直接积分法和极限状态法（JC法）假设堤前洪水位服从P-Ⅲ型分布并利用实测堤前水位确定分布参数，需要足够的实测资料，而随机微分方程法直接忽略了区间洪水的影响。此外，感潮河段与一般内陆河流不同，在河口潮位变化幅度较大的地区，日变化幅度可达4 m，河道内水位多变。本研究在缺乏实测堤前水位资料情况下，运用随机模拟法（MC法）分析洪水不确定性、潮位不确定性及风浪不确定性，结合水力计算考虑区间洪水影响，建立感潮河段漫堤风险率计算模型，并运用于实际堤防工程。

1 感潮河段漫堤风险率的影响因素分析

洪水漫堤是指堤前洪水位超过河、湖堤顶高程，越过堤顶的现象[2]。堤防的洪水漫堤风险率是指由洪水造成的漫堤事件发生的概率。

设H为堤前最高水位，Z为堤顶高程，漫堤风险率可表示为P（H>Z），其中

H=h+e+R

（1）式中：h为堤前静洪水位：e为风荷载引起的风壅高度：R为风荷载引起的波浪爬高。

一般来说堤前最高静水位^与洪峰流量、河道特性有关，对于感潮河段，还受潮位影响。风壅高度e和波浪爬高R主要受风荷载影响。因此，洪峰流量、潮位、风浪和河道特性是影响漫堤风险率的主要因素。

洪水是一种随机水文现象，其不确定性主要从洪峰流量、洪量和洪水历时3个要素考虑，它们之间存在相互联系。在堤防设计过程中，设计洪水过程一般可以由典型洪水过程按洪峰流量同倍比放大得到。这时，针对洪水因素不确定性，可根据长序列洪水资料，研究洪峰的概率分布。

潮位是一种具有一定周期性的水文现象，一般需要从高低潮位、潮差、潮时3个要素进行考虑，对于堤防工程，一般主要考虑最高潮位。在堤防设计过程中，设计潮位过程可以通过以年最高潮位为控制要素、按同倍比法放大典型潮位过程得到。针对潮位因素的不确定性，可根据潮位站长序列潮位资料，研究年最高潮位的概率分布。

风浪也是一种随机现象，其不确定性需要从风向、风速和风区长度3个要素综合考虑。在堤防风浪超高设计中，一般采用年最大风速，风区长度的确定需要考虑主风向和计算点位置。分析风速因素的不确定性，主要是根据长序列风资料研究年最大风速的概率分布。在此基础上，可进一步研究风荷载引起的水位壅高和波浪爬高的特性。

河道特性包括河道过水断面、河道糙率系数、局部阻力等。河道严重淤积、建筑物阻水或盲目围垦都会影响河道过水断面，河滩种植会增大河道糙率系数。在堤防设计过程中，一般依据实测断面或设计断面确定河道过水断面，依据护面类型或利用实测河道水位一流量关系率定糙率。分析河道特性，主要是检验河道特征相关资料的准确性。

基于以上分析，运用蒙特卡罗法结合水力计算，研究在河道特性确定情况下，洪水不确定性、潮位不确定性和风浪不确定性对感潮河段漫堤风险率的影响。

2 蒙特卡罗（ MC）法计算漫堤风险率

2.1 洪水模拟

在我国，一般认为洪峰流量服从P-Ⅲ型概率分布，其概率密度函数为C_V、C_S分别是x的均值、变差系数和偏态系数，可根据长序列实测洪峰资料采用矩法或适线法得到。

应用蒙特卡罗法随机模拟[4]分析时，可利用“舍选法”[5]生成服从P-Ⅲ型分布的m个随机洪峰流量值，然后根据同倍比法放大典型洪水过程线，得到m场洪水过程。

2.2 潮位模拟

一般认为，在海岸地区年最高潮位服从极值I型概率分布，在潮汐河口地区年最高潮位服从P-Ⅲ型概率分布[6]。感潮河段属于潮汐河口地区，年最高潮位可认为服从P-Ⅲ型概率分布。

进行潮位随机模拟时，与洪水随机模拟相似，可采用“舍选法”生成服从P-Ⅲ型分布的n个随机年最高潮位值，然后根据同倍比法放大典型潮位过程线，便可得到n场潮位过程。考虑到同倍比放大法对低潮位的影响，也可采用改进的变倍比放大法[7]放大典型潮位过程。

2.3 风浪模拟

年最大风速一般认为服从最大值分布中的极值I型分布[8]，其概率密度函数为

E（x）可由《堤防工程设计规范》中波高公式C.1.21和波浪爬高公式C.3.1 -1，根据给定的风速和风区长度求得。根据波浪爬高均值，计算得分布参数μ，进而可确定波浪爬高的瑞利分布函数。应用蒙特卡罗模拟方法进行模拟分析时，对每个风速可随机产生j个波浪爬高值，则一组风速（i个）可随机产生i×j个波浪爬高值。

2.4 漫堤风险率计算

为进行感潮河段漫堤风险率计算，需通过河道水力计算，确定有关断面最高水位。为此，利用Preissmann隐式差分格式，根据“追赶法”[11]建立水力计算模型。对上游有闸、坝等水T建筑物的河道，模型以随机模拟生成的m场洪水经调洪计算[10]后的下泄流量过程Q_i泄-t为上边界：对没有闸、坝等水工建筑物的天然河道，模型直接以随机模拟生成的m场洪水过程Q_i-t为上边界。将洪水和潮位视为相互独立的事件，对每个上边界分别以随机模拟产生的n场潮位过程S_i-t为下边界，区间洪水以集中人流形式汇人河道。通过模型进行洪水演进计算后，对于每个上边界各断面可得到n个最高静洪水位h，对m个上边界各断面则有m×n个最高静洪水位h。

对于每一个堤前最高静洪水位，考虑风浪因素的影响，进行风浪模拟，得到i个风壅高度e和i×j个波浪爬高值R，代人式（1），可得i×j个堤前最高水位。对于m×n个最高静洪水位则有m ×n×i×j个提前最高水位。比较堤前最高水位与堤顶高程，并统计H>Z的个数（设为k），则漫堤风险率为

3 工程实例

3.1 工程概况

某河流位于我国东南沿海地区，干流长35 km，上游建有A水库，承担下游防洪任务，下游防洪标准为20 a一遇。洪水期间，水库根据坝址至下游控制断面区间洪水情况进行补偿调度。根据坝址多年洪水资料，计算得到年最大洪峰流量均值x= 835 m3/s，变差系数C_V= 0.57，偏态系数C_S=1.42，不同频率的洪峰流量见表1。

河流人海口以上7.5 km内为感潮河段，根据河口多年潮位资料，计算得到年最高潮位均值为4.85 m，变差系数C_V= 0.14，偏态系数C_S=0.75，不同频率的年最高潮位见表2。感潮河段平均河宽为105 m，两岸有四级堤防，防洪标准为20 a一遇，该河段3个控制断面资料见表3。实测多年年最大风速均值为23.9 m/s，均方差为6.2，多年年最大风速均值相当于10级风力，主风向为东南偏东。

3.2 漫堤风险率计算

（1）随机生成1 000个洪峰流量（m=1 000）和500个最高潮位（n= 500），洪峰流量概率分布见图1，最高潮位概率分布见图2。运用同倍比放大法生成1 000场洪水过程和500场潮位过程，对1 000场洪水按照水库调度规则进行调洪计算，得到水库下泄流量。以水库下泄流量为上边界，对每个上边界，工况1分别以年最高潮位均值采用同倍比放大法得到的潮位过程为下边界，工况2分别以随机模拟产生的500场潮位过程为下边界，各工况区间洪水均以集中旁侧人流形式汇人河道，建立水力计算模型，进行洪水演进计算，得到各控制断面堤前最高静水位。

（2）对于每一个堤前最高静洪水位，考虑风浪因素模拟生成i个风速和风壅高度以及i×j个波浪爬高（i =100，j=100）。风壅高度概率分布见图3，波浪爬高概率分布见图4，可以看出风壅高度远远小于波浪爬高。在堤前最高静水位基础上，考虑风壅高度和波浪爬高，由式（l）计算各断面堤前最高水位。

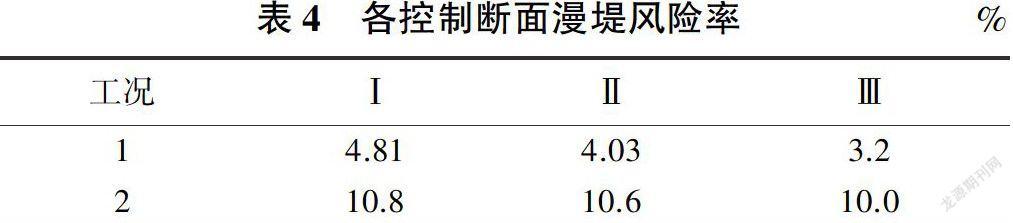
（3）统计各控制断面超过堤顶高程的最高静水位和最高水位个数，由式（7）计算得到各工况漫堤风险率，计算结果见表4。

由表4可知，工况1各控制断面漫堤风险率均不到5%，说明当下游潮位按年最高潮位均值对应的确定性条件考虑时，该感潮河段堤防满足20 a一遇的设计防洪安全标准：工况2各控制断面漫堤风险率相近，约为10%，说明当下游潮位按不确定性条件考虑时，该感潮河段堤防达不到20 a一遇的设计防洪安全标准。工况2与工况1中同一断面的漫堤风险率数值之差即为考虑潮位不确定性而增加的堤防防洪安全风险。此外，该差值随着断面位置接近人海口而逐渐增大，即控制断面越靠近人海口，漫堤风险受潮位影响越明显。

考虑潮位不确定性后，堤防漫堤风险率有所提高，为保障堤防安全，可通过工程措施加高堤防。经分析，不同堤防增高量对降低漫堤风险率的效果见图5。

图5表明，随堤顶增高量的加大，各控制断面的漫堤风险率逐渐减小，进而堤防防洪安全性逐渐提高。断面I、断面Ⅱ漫堤风险率随堤顶增高量加大而逐渐接近，其原因可能是两控制断面位置比较接近。当堤顶加高量达到0.5 m时，3个控制断面的漫堤风险率均可控制在5%左右，该段堤防的防洪安全性基本上达到设计防洪安全标准。

4 结语

本研究分析了影响感潮河段漫堤的风险因素，将洪峰流量、最高潮位、风壅高度和波浪爬高作为随机变量，讨论了它們的概率分布及参数确定方法，运用蒙特卡罗法结合水力计算，建立了感潮河段漫堤风险率计算模型，并运用于实际堤防工程漫堤风险率计算。结果表明：考虑潮位不确定性，漫堤风险率有所提高：堤段越靠近人海口，漫堤风险受潮位影响越明显，适当加高堤防可有效降低感潮河段漫堤风险。

参考文献：

[1] 赵庚润，李羽文，崔冬，等.黄浦江上海市区段防汛墙漫溢风险分析[J].水利水电科技进展，2016，36（5）：57-67.

[2]高延红，张俊芝.堤防工程风险评价理论及应用[M].北京：中国水利水电出版社.2011：48-51.

[3] 詹道江，徐向阳，陈元芳.T程水文学[M].北京：中国水利水电出版社.2010：100- 200.

[4] 何淑军，张春山，吴树仁，等.基于蒙特卡罗法的多级黄土滑坡可靠性分析[J].地质通报，2008，27（ 11）：1822-1831.

[5] 王文圣，丁晶，金菊良.随机水文学[M].北京：中国水利水电出版社.2008：52-53.

[6] 中华人民共和国水利部.堤防T程设计规范：GB 50286-2013[S]。北京：中国计划出版社，2013：46-48.

[7]陈静.设计潮位过程线及其推求[J].水文，2012，32（3）：47-50.

[8]李其军，陈肇和.土石坝漫坝风险理论与应用[M].北京：中国水利水电出版社，2008：16- 24.

[9]侯一筠，段永亮，陈更新，等.浅水非线性随机海浪的波高分布[J].中国科学：地球科学，2009，39（ 12）：1795-1800.

[10]顾圣平，田富强，徐得潜.水资源规划及利用[M].北京：中国水利水电lJ版社.2009：111- 141.

[11]王船海，李光炽.实用河网水流计算[M].南京：河海大学出版社，2006：65-75.