考虑漫溢过程的一维堤防溃决分洪计算研究

张涛 单既连 亓立云 胡方

摘要：以平原河道梁济运河为例，考虑漫溢过程进行河道堤防溃决分洪计算。对于由缺口漫溢演變为溃堤的堤防溃决，简化为先漫溢、后溃堤的两阶段溃决过程，河道洪水演进采用MIKE11 -维水动力模型，溃决分洪按侧堰自由出流计算。在既定的水力条件及假定溃口尺寸条件下，计算漫溢、漫溃、瞬溃等3种溃决形式的分洪流量、水位过程，相对于一阶段的瞬溃方案，二阶段的漫溃方案的溃决分洪水量较大、溃决时间较长，较符合河道堤防溃决发展过程。

关键词：漫溃联算；漫溢；平原河道；MIKE11

中图分类号：TV131

文献标志码：A

doi： 10.3969/j.issn.1000-1379.2018.06.012

堤防工程是河道防洪工程体系的重要组成部分，通过修建堤防可有效顺导水流，避免河道洪水淹没两岸区域。在堤防缺口段、险工段，存在发生洪水漫溢或堤防垮塌的可能性，堤防溃决将给沿岸地区带来人民生命及财产损失。目前在大坝溃决演变机理1、溃决洪水一维及二维演进[2.3]等方面研究成果较多，在河道堤防溃决方面，张秀勇[4]研究了黄河下游堤防冲刷破坏机理，房殿荣[5]通过土体冲刷试验分析河道堤防溃口破坏过程。鉴于河道堤防溃决事件较少，以及受堤防材质、水文水力条件等不确定性因素影响，常对溃决演变过程、溃决尺寸等进行简化或假定[6]。本文以平原河道梁济运河为例，假定溃口尺寸，考虑缺口漫溢过程进行溃堤分洪计算，分析比较漫溃与漫溢、瞬溃等溃决形式的分洪流量、水位过程。

1 溃决形式

根据堤防溃决发生原因，溃决可分为三大类：一是漫溢溃决[4]，当洪水位超过堤顶或堤防缺口时，形成洪水漫溢：二是渗透溃决，洪水水力渗透导致堤防发生渗水、管涌、流土等，逐步形成溃口，造成溃决[4]；三是冲刷溃决，如在急流段、弯道险工段，洪水冲刷淘空堤身逐步形成溃口，造成堤防溃决。实际堤防溃决发展过程中，各溃决形式常常相互伴随发生，如当堤防缺口发生洪水漫溢时，随着洪水长时间冲刷缺口两侧边坡及缺口底部，缺口可能会逐渐扩大，形成大规模溃决；在弯道水流冲刷堤防过程中，洪水同时会渗透堤防，造成堤防失稳垮塌。

根据溃决发展过程，溃决可分为瞬溃和渐变溃。受地震等因素影响，可能会导致堤防瞬间垮塌溃决：河道堤防多为土质堤防，溃口通常为逐步发展形成，溃决一般为渐变溃。

2 考虑漫溢过程的堤防溃决分洪模型

2.1 漫溃发展过程

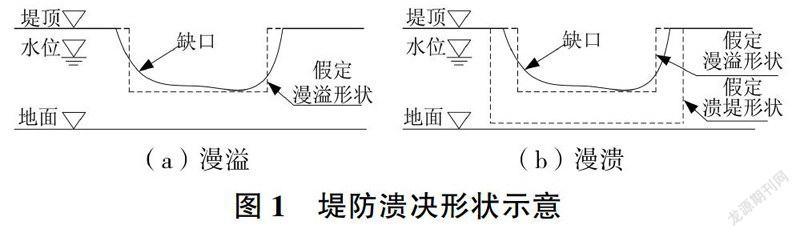
相对于山丘河道，平原河道一般比降较小、洪水流速较小，堤防受洪水瞬间冲垮破堤的现象较少。平原河道岸线多为地上土质堤防，鉴于河道沿线居民生产耕作以及交通要求，部分堤段常留有过路缺口，或地面局部沉降塌陷导致部分堤段下沉形成大段缺口7，在遭遇大洪水时缺口段可能发生洪水漫溢。随着漫溢水流不断冲刷，缺口或者基本维持现状尺寸，即漫溢不溃：或者缺口纵向发展，加大溃决深度：或者缺口横向发展，造成缺口两翼堤坡垮塌，由漫溢演变为溃堤。溃决过程受筑堤土料、修筑质量、坡面防冲设施以及洪水水力条件等因素影响。为简化计算，溃口及漫溢口形状均假定为矩形，漫溢及漫溃形式见图1。

对于由漫溢演变为溃堤的溃决，本文简化为两阶段的漫溃过程，即先漫溢、后溃堤。在溃堤前为漫溢过程，即自由出流：在水位达到保证水位时刻瞬间溃堤，其中，保证水位根据河道现状防洪能力确定，当洪水位达不到保证水位时则确定溃堤在洪峰来临时刻瞬间溃堤。

2.2 溃决高程及宽度

（1）漫溢口。为简化计算，漫溢口根据现状缺口过水断面尺寸等效概化为矩形。漫溢底高程Zf取缺口处底高程，不低于堤外附近地面高程：漫溢宽度B_f，近似按以下公式计算：式中：A_g为缺口过水断面面积，m2；Z_d为堤顶高程，m。

（2）溃口。溃口底高程Z_b，不低于堤底高程，不低于堤外附近地面高程。溃口宽度结合经验公式及专家咨询意见综合确定，文献[8]推荐的汇流点处溃口宽度B_b经验公式为

B_b=4.5（lgB）^3.5+50

（2）式中：B为河道宽度，m。

2.3 水力计算方法

（1）河道洪水演进。根据洪水源汇过程，采用MIKE 11 一维非恒定流水动力模型[9]进行洪水演进计算。该模型基于圣维南方程求解，其连续方程、动量方程分别为式中：A力河道过水断面面积，m2；Q为流量，m3/s；u为侧向来流在河道方向的流速，m/s；t为时间，s；x为沿水流方向的水平坐标；g为河道的侧向来流量，m3/s；α为动量修正系数；g为重力加速度，m/s2；y为水位，m；S_f为摩阻坡降。

该模型使用6点abbott -lonescu格式隐式差分离散圣维南方程组[9]，适应于分汊型河道等复杂河网的水力计算，模型计算精度较高，收敛性较好[3]。

（2）溃决分洪流量。当溃口底高程低于堤外周围区域高程时，影响溃口分洪出流形态，易形成淹没出流：当溃口底高程高于周围地面时，溃决洪水能向周边区域顺利下泄，溃决洪水流态基本为自由出流。本次研究均采用侧堰公式[10]计算分洪流量过程，公式为式中：m为自由溢流的流量系数；σ为淹没系数；Q_b为决口处出_：流流量，m3/s；Z为决口处河道水位，m；Z_b为溃口底高程，m；b为溃决宽度，m。

（3）漫溢溃堤分洪联合计算。漫溢及溃堤分洪过程采用MIKE11中的侧向溃坝模块模拟。将溃口处的堤防视为漫溢口，即堤防长度设为漫溢口宽度，堤顶高程设为漫溢高程，漫溢洪水为自由出流：当水位达到保证水位或洪峰来临时刻开始溃堤，将溃口初始形状及终止形状均设为同一溃口形状，即在溃堤开始瞬间，溃口底高程及溃口宽度瞬间形成，溃堤洪水为自由出流。

3 溃决分洪实例计算

3.1 河道情况

梁济运河是山东省南四湖流域北部地區一条承担防洪排涝、输水航运等任务的骨干河道，于流全长87.8km，流域面积3 306 km2。该河道为季节性平原河道，洪水主要由当地暴雨形成，洪水涨落比较缓慢，汇集消退时间较长。流域内地形基本为北高南低，干流堤顶高程在20 a-遇洪水位以上1～3 m，支流郓城新河口段堤防防洪标准相对较低，堤防较单薄，为土质堤防：同时，堤防存在道路缺口，缺口处路基为土路结构。在于流桩号42+030郓城新河口设置1处溃口（见图2）。

3.2 漫溢口及溃口尺寸

（1）漫溢口。现状缺口呈不规则梯形，缺口上部宽约为55 m，下部宽约为42 m，缺口底最低处高程为38.5 m。根据断面尺寸概化方法，并适当考虑缺口受洪水冲刷不断扩大等因素，确定漫溢口宽度为50 m，漫溢口底高程为38.5 m。

（2）溃口。根据式（2）计算溃口宽度为164 m，考虑到历次堤防加固情况并结合专家咨询意见，确定溃口宽度为120 m，溃堤底高程为37.7 m。

3.3 计算方案

（1）计算方案。为分析不同溃决形式下的分洪过程，设定漫溢、漫溃及瞬溃3种溃决计算方案，其中瞬溃方案假定堤防按纯溃堤形式，不考虑缺口漫溢过程，当水位达到保证水位或洪峰来临时刻时瞬间溃堤。洪水计算频率选取20 a一遇、50 a一遇标准。

（2）水力参数。对梁济运河0+000-86+800河段建立MIKE 11一维水动力模型，设置河道、洪水、建筑物、糙率等参数。河道断面间距为100～200 m；设置流畅河、郓城新河等主要支流的洪水设计过程为洪水汇人点源，闸坝均按敞泄控制。河道采用分区糙率，河槽糙率为0.023、滩地糙率为0.035。20 a一遇、50 a一遇洪水河口起始水位分别为36.29、36.79 m。梁济运河现状防洪标准基本达到20 a一遇洪水标准，河道保证水位采用20 a一遇洪水设计水位，其中郓城新河断面处保证水位为40.08 m。

3.4 计算结果

20 a一遇洪水（p=5%）、50 a一遇洪水（p=2%）下的溃决流量、水位过程见图3～图6。

按照漫溃方案，在20 a一遇洪水下，随着河道水位的增高，先发生漫溢：当洪峰来临时，由漫溢瞬间演变为溃堤，溃口过水断面瞬间扩大，溃决流量为最大，与瞬溃方案同时溃决：随着洪水的消退，溃决流量逐渐减小直至为零。在50 a-遇洪水下，随着河道水位的增高，先发生漫溢：当河道水位超过保证水位时，由漫溢瞬间演变为溃堤，溃口过水断面瞬间扩大，溃决流量急剧加大，形成初次溃决洪峰：在洪峰时刻分洪流量达到最大，形成二次溃决洪峰：随着洪水的消退，溃决流量逐渐减小直至为零。

3.5 分洪参数分析

漫溢、漫溃及瞬溃方案的溃决特征值见表1。漫溃方案的溃决流量、水位过程见图7。

（1）溃决发展过程。同一量级洪水下，漫溃方案的溃决时长为最长。漫溃与漫溢方案中，漫溢阶段的分洪流量、水位过程均一致：漫溃与瞬溃方案中，溃堤初始阶段的分洪流量、水位过程有所差异，但分洪过程逐渐趋于一致。

（2）分洪洪峰。同一量级洪水下，瞬溃方案的分洪洪峰为最大，漫溃次之，漫溢为最小。漫溃方案中，在漫溢阶段，溃决处河道水位相比未发生溃决时的河道水位有所下降，溃堤时的分洪水头相对于瞬溃方案溃堤时的分洪水头较小，因此分洪洪峰流量相对较小。

（3）分洪水量。漫溃方案的分洪水量为最大，瞬溃次之，漫溢为最小。漫溢方案中，仅有漫溢口分洪，由于漫溢高程相对较高、漫溢口宽度较窄，因此同量级洪水标准下其分洪水量为最小。一般情况下，溃决分洪水量越大，造成的淹没范围越大，淹没历时越长，将造成的洪灾损失越大，相对于漫溢及瞬溃方案，漫溃方案对防洪安全尤为不利。

（4）溃决事件验证分析。一般平原河道发生堤防垮塌的可能性较小，在堤防过路缺口、局部堤高不达标等堤段，遭遇大洪水可能发生漫溢而不溃堤：或是漫溢后，冲刷、渗透破坏等因素导致漫溢演变为溃堤。据资料记载，该流域1964年8月普降大雨，造成支流郓城新河河口段漫溢决口，口门宽约为40 m；1957年、1993年及2004年等年份，强降雨导致郓城新河等多条支流漫溢受灾。鉴于河道溃决事件发生较少，缺少溃决演变过程、流量等实测数据，同时考虑溃口演变机理的复杂性[1，6]，本文假定不同的演变过程及溃口尺寸以简化计算。

4 结语

（1）在土质堤防缺口段随着漫溢水流不断冲刷漫溢口，漫溢口可能在纵向及横向发展，由漫溢演变为溃堤。在既定条件下，对比分析了漫溃与漫溢、瞬溃等溃决形式的分洪流量及水位过程，相对于一阶段过程的瞬溃形式而言，采用简化的两阶段漫溃形式更符合溃决发展过程：同量级洪水条件下，漫溃的分洪水量为最大、溃决时长较长，将造成更大的洪灾淹没损失。

（2）本文对溃决分洪流量是按侧堰自由出流计算的，未考虑淹没区洪水演进对河道溃决分洪的水力影响，应探讨河道一维洪水与淹没区二维洪水的耦合计算，进一步研究堤防溃决演变机理。

参考文献：

[1]王光谦，王永强，刘磊，等.堰塞坝及其溃决模拟研究评述[J].人民黄河，2015，37（9）：1-7.

[2]黄金池，何晓燕.溃坝洪水的统一二维数学模型[J].水利学报，2006，37（2）：222-226.

[3] 沈洋，王佳妮.基于MIKE软件的溃坝洪水数值模拟[J].水电能源科学，2012，30（6）：56-59.

[4] 张秀勇.黄河下游堤防破坏机理与安全评价方法的研究[D].南京：河海大学，2005：56-64.

[5]房殿荣.黄河下游堤防溃口土体的冲刷性能[D].郑州：郑州大学.2010：46 - 51.

[6] 张社荣，张婷.考虑调洪的一维漫顶不溃与漫顶溃坝过程模拟[J].白然灾害学报，2012，21（4）：33-39.

[7] 朱庆川，高瑞芳，尹桂强，等.地面沉降对河道堤防的影响及应对措施[J].地质灾害与环境保护，2010，21（4）：7-11.

[8] 国家防汛抗旱总指挥部办公室.洪水风险图编制技术细则附录（试行）[Z]北京：国家防汛抗旱总指挥部办公室，2013：15 - 16.

[9]

Danish Hydraulic Insititute.MIKE llReference Manual[M].Copenhagen：DHI，2014：170-172.

[10] 李炜.水力学计算手册[M].北京：中国水利水电出版社，2006：73-75.