黄河中游吴堡一龙门段河道洪水概化预报研究
黄华平 侯博 梁忠民 李彬权 王军


摘要:将洪水过程模式概化与支持向量回归机相结合,提出了一种逐时段更新的河道洪水概化预报方法。以黄河中游吴堡一龙门段河道洪水预报为例,根据龙门站1980-2000年28场洪水过程资料概化出典型洪水模式,采用支持向量回归机算法构建洪峰流量与洪水历时的预报模型,根据逐时段洪峰流量/洪水历时的预报结果,对概化的典型洪水模式进行缩放,实现了龙门站洪水过程主要特征的概化预报。对2001-2006年5场洪水的预报检验结果表明:随着逐时段资料的更新,该方法的预报精度逐步提升,且涨水阶段的预报结果已能较好地展示整场洪水过程的发展趋势。
关键词:支持向量回归机:概化预报:洪水:吴堡一龙门区间:黄河中游
中图分类号:TV122;TV882.1
文献标志码:A
doi:10.3969/j.issn.1000-1379.2018.06.008
1 引言
黄河中下游洪水陡涨陡落,含沙量变幅大,河床冲淤变化剧烈,河道洪水演进规律的复杂性给汛期防洪带来严重影响[1-2]。目前,关于黄河中下游河道洪水演进规律研究已有大量成果,如:赵连军等[3]采用非恒定洪水演进数学模型,在黄河下游河道开展了汛期洪水演进预测及演进实时作业预报:刘华振等[4]采用馬斯京根分段连续演算法,模拟了黄河吴龙区间(吴堡一龙门区间)洪水过程:贺莉等[5]采用一维水动力学模型分析了黄河吴堡一潼关河段洪水传播时间与洪水量级的关系:李肖男[6]等采用三维水沙数学模型,对黄河下游花园口一艾山河段不同治理方案下场次洪水的演进过程、河道冲淤及分洪退水过程进行了模拟计算:张晓雷等[7]采用平面二维水沙数学模型,在黄河下游河道现存生产堤条件下对典型洪水进行了模拟计算。
考虑到黄河中下游河道洪水预报的复杂性,本文将洪水过程模式概化与支持向量回归机( SupportVeCtor machine for Regression,SVR)相结合,构建了一种简单、快速的河道洪水概化预报方法。选取1980-2000年28场洪水作为率定资料概化了典型洪水过程,并训练了基于支持向量回归机的洪峰流量/洪水历时预报模型,将2001-2006年间的5场洪水作为验证资料,采用该方法进行了预报检验,并将预报结果与实测洪水过程进行了比较。
2 洪水模式概化
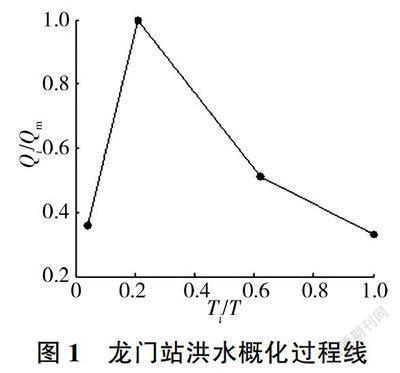
概化洪水过程线是根据待预报站点的实测洪水过程线资料进行综合分析后得出的具有一定代表性的洪水过程线模式[8]。具体做法:首先,将各场次洪水过程线绘在同一幅图上,纵坐标表示流量相对数Q/Qm(Qi为i时刻的流量,Qm为最大流量),横坐标表示时间相对数Ti/T(Ti为i时刻的洪水历时,T为洪水过程总历时),然后将峰现时间重叠在一处,选用其中常见且能概括该站洪水形状特征的平均过程线作为概化过程线。龙门站1980-2000年28场洪水过程线的概化结果见图1。
3 基于SVR的洪峰/历时预报模型
3.1 支持向量回归机
SVR是建立在支持向量机(SVM)上的回归算法,其基本思想是用少数支持向量代表整个样本集,利用非线性映射ψ(x)将低维非线性函数估计问题转换为高维线性函数估计问题[9-10]。
已知一个训练集X={(X1,y1),(x2,y2),…,(xn,yn)} Rn×R,设其在高维特征空间的线性回归函数为
f(x)=[ω,ψ(x)]+b (ω,x ∈Rn;6∈R) (1)式中:x为样本输入;ψ(x)为x的非线性映射;[ω,ψ(x)]为ψ(x)的线性多项式;ω为多项式系数;b为截距。
可以把不敏感损失函数ε范围内的回归估计问题定义为对一个损失函数进行风险最小化的问题,即最优的回归函数是在一定约束条件下的最小化规则化风险泛函,通过引入非负松弛变量ξi:及ξ*i,最小化规则化风险泛函可以描述为
.
式中:C为误差惩罚系数。
此时约束条件为
误差惩罚参数C可起到调节模型复杂度和训练误差的作用,取值太小或太大,将出现“欠学习”或“过学习”现象,使训练误差增大、泛化能力减弱;核参数σ反映了训练样本数据的分布特性,确定了局部领域的宽度。因此,SVR回归问题的推广性能取决于误差惩罚参数C与核参数σ。由于遗传算法( GenetiC Algo-rithm,GA)在复杂的优化问题中只需构造一个适应度函数,就可通过选择、杂交、变异等遗传机制,完成对问题最优解的白适应搜索过程,且算法成熟,在水文中应用广泛,因此本次选择构建GA-SVR算法进行参数优选,这样既可保证参数的准确性,又可保证计算的时效性。算法流程见图2。
3.2 预报因子挑选
龙门站洪水的主要来源分为三类:干流上游来水、区间人流及无控区域降水。研究中将吴堡站对应场次洪水作为干流上游来水,选取白家川、甘谷驿、后大成、裴沟和延川站作为支流典型站,由于这些站点汇流至龙门站的历时大致相同,因此将这5个站的流量合并作为区间人流量。甘谷驿站以下至龙门站区域为无控区域,选取该区域内10个雨量站(柏坡底、大宁、河底、吉县、李家山、王家窑、张川河、桐湾、郭家垛、坡头),采用泰森多边形法计算该区域面平均雨量。采用相关系数显著性检验表确定初选因子,之后采用逐步回归法对初选因子作进一步筛选,确定最终的预报因子。洪峰流量/洪水历时的预报因子见表1。
3.3 模拟与验证结果
将Matlab作为编程平台,挑选出龙门站1980-2006年33场洪水的对应预报因子。其中:1980-2000年的28场洪水作为率定资料,用于训练GA -SVR模型:2001-2006年的5场洪水作为验证资料,采用训练完毕的GA -SVR模型对其洪峰流量及洪水历时进行预测。选用相对误差作为模型的评价指标,率定期及验证期模型的计算结果见表2、表3。
由表2、表3可看出,在28场率定洪水中,洪峰流量相对误差小于20%的有23场,洪水历时相对误差小于20%的有16场,洪峰流量和洪水历时的合格率分别为82.1%和57.1%:5场验证洪水中,洪峰流量相对误差小于20%的有4场,洪水历时相对误差小于20%的有3场,洪峰流量和洪水历时的合格率分别为80.0%和60.0%。结果表明,采用GA-SVR模型对龙门站洪水的洪峰及历时进行预报是可行的。
4 洪水过程预报示例
本文引人逐时段(△t=l h)更新预报的方法,具体步骤如下。
(1)从洪水起涨时刻开始预报,挑选预报因子时,将吴堡站和区间人流对应场次洪水初始时刻至当前时刻的最大洪水流量作为该站(或区间)当前时刻的洪峰流量,初始时刻至当前时刻的洪量作为该站(或区间)当前时刻的洪量,初始时刻至当前时刻的历时作为该站(或区间)当前时刻的洪水历时,其他预报因子进行类似处理。
(2)将已确定的预报因子导人已训练完毕的洪峰流量/洪水歷时预报模型中,预报当前时刻的洪水洪峰及洪水历时。
(3)使用当前时刻预报的洪峰流量及洪水历时,对已概化的龙门站典型洪水模式进行相应缩放,将缩放结果作为当前时刻的洪水过程预报结果。
(4)随着洪水资料的不断更新,重复步骤(1)~步骤(3),直至整场洪水结束。
以龙门站“20040727”洪水为例,分别列出从洪水起始时刻起(作为0时刻)第2、第6、第13及第27时刻的洪水过程预报结果,见图3。
由图3可以看出:①随着时段推移,资料不断更新,逐时段更新预报方法结果的精度呈上升趋势,整体体现出“越报越好”的预报效果:②在洪峰出现时刻前(第6时刻),预报的洪水流量过程与实测流量过程相差已较小,说明在洪水起涨时段,该方法的预报结果已能较好地描述整场洪水的发展过程:③洪峰预报精度随着时段推移不断提升,之后趋于平稳:④对于洪水历时的预报,随着时段推移其吻合程度总体呈稳步上升趋势,直至该场洪水结束。
5 结语
将洪水过程模式概化与支持向量回归机相结合,提出了一种逐时段更新的河道洪水概化预报方法。选取龙门站1980-2000年间的28场洪水作为率定资料,用于概化典型洪水过程及构建基于GA-SVR的洪峰流量/洪水历时预报模型,并对2001-2006年的5场洪水进行了预报检验。结果表明:①随着洪水资料的不断更新,该方法的预报精度呈上升趋势,整个预报过程呈现出“越报越好”的预报效果:②实时预报过程中,随着时段推移,洪峰流量预报精度逐渐上升,之后趋于平稳,在洪水过程的涨水段,该方法已能较好地体现整场洪水过程的发展趋势。
本文研究的是一种洪水过程的概化预报方法,侧重的是洪峰、洪水过程主体形状的预报,具有简单.快速等特点。但是,本文仅概化了单峰洪水模式,对于模式更复杂的洪水(如复式洪水过程)还需要进一步研究。
参考文献:
[1]赵卫民.黄河中下游暴雨洪水情报预报原型系统[J].人民黄河,1994,16(8):12-14.
[2]李彬权,牛小茹,梁忠民,等.黄河中游干旱半干旱区水文模型研究进展[J].人民黄河,2017,39(3):1-4.
[3] 赵连军,江恩惠,董其华,等.数学模型在黄河下游河道洪水演进预报中的应用[J].四川大学学报(T程科学版),2007,39(1):6-12.
[4] 刘华振,刘俊,左君,等.马斯京根法在黄河吴堡一龙门区间洪水演算中的应用[J].水电能源科学,2012,30(6):53-55.
[5] 贺莉,傅旭东.黄河吴堡一潼关河段洪水传播时间的沿程分布[J].南水北调与水利科技,2012,10(1):18-26.
[6]李肖男,张红武,钟德钰,等.黄河下游河道治理三维数值 模拟研究[J].水利学报,2017,48( 11):1280-1292.
[7] 张晓雷,张英克,孙东坡.黄河下游典型河段滩槽分界二维洪水数值模拟[J].水利水电技术,2013,44(7):120.
[8]梁忠民,钟平安,牮家鹏.水文水利计算[M].北京:中国水利水电出版社.2008:111- 112.
[9] VAPNIK V.Estimation of Dependences Based on EmpiricalData[M]. New York: Springer Science&Business Media,2006:181-230.
[10]
VAPNIK V.The Nature of Statistical Leaming Theory[M].New York: Springer Science&Business Media, 2013:267-287.

