考虑库水可压缩性的重力坝地震动力响应分析

李渤 辛全才

摘要：为研究库水压缩性对坝体动力特性的影响，以某重力坝为例，建立4种不同库水作用有限元模型。对比传统的附加质量模型、折半修减的附加质量模型和忽略库水压缩性模型得到的坝体自振频率、坝体关键部位峰值应力与位移及坝面的动水压力分布，表明：附加质量模型在一定程度上夸大了水体的作用，导致坝体的基频降幅最大，增大了坝踵部位的峰值应力，对坝体中上部的动水压力有明显的放大现象，但对坝顶位移有一定的削弱；可压缩库水模型可以更好地反映库水与坝体之间的相互作用，因此在计算中不应忽略库水的可压缩性影响。

关键词：重力坝；动水压力；流固耦合；动力特性；库水可压缩性

中图分类号：TV312；P315.9

文獻标志码：A

doi：10.3969/j.issn.1000-1379.2018.08.027

我国水力资源有70%～80%集中在西南地区，这些地区是地震灾害频发区。在这些地区建设大型水利水电项目，结构的抗震安全无疑是T程建设的关键。坝体一库水系统的耦合作用是混凝土大坝抗震安全评价研究的热点之一。自Westergaard给出著名的动水附加质量公式之后，诸多学者通过数值模拟与试验对坝体上游坝面动水压力的问题进行了深入研究，大量的研究表明库水可压缩性、坝体一地基相互作用、库底淤沙吸能作用等都会对上游坝面的动水压力产生不同程度的影响。

鉴于问题的复杂性，目前关于动水压力对坝体地震反应影响问题未能得到合理解决。陈厚群等通过振动台模型试验，校验了流固耦合模型与Westergaard附加质量模型的结果，表明附加质量模型所得结果偏大，而流固耦合有限元模型得出的结果与试验结果较为符合。黄耀英等对两种库水附加质量模型的混凝土重力坝动力响应进行研究，认为传统Westergaard附加质量模型折半计算后得到的坝体自振特性较直接使用Westergaard附加质量模型计算的精度高，但未计入库水的可压缩性。赵兰浩等结合实际T程给出考虑库水可压缩性时高拱坝动力特性的数值求解方法，表明库水的可压缩性对坝体的白振频率和振型等动力特性有较大影响，但未提及库水压缩性对坝体应力分布和位移的影响。杨柳等探讨了库水可压缩模型对拱坝动力响应的影响，并与传统附加质量模型运算结果进行对比，结果表明，附加质量模型夸大了动水压力作用，对顺河向位移和竖直向位移有一定影响。

因此，开展坝体一库水流固耦合作用问题与West—ergaard附加质量模型的适用性、精度和两者之间的差异性分析具有一定意义。

1 坝面动水压力数值模拟方法

1.1 Westergaard附加质量模型

Westergaard研究了垂直刚性坝面在水平简谐地面运动下的动水压力，并给出著名的动水附加质量公式：式中：mw（h）为水深h处的库水附加质量；P为水的密度；Ho为库水深度；h为计算点的水深。

1.2 库水有限元流固耦合模型

假定流体为均质、无旋无黏且可压缩的理想流体，在仅考虑小变形的情况下流速远小于流体中声速，可得到以压力P为目标函数的波动方程：式中：△为拉普拉斯算子：P为动水压力：c为流体中声速，c=√k/p（K为流体体积模量，p为流体密度）；P为动水压力的二阶导数。

式（2）需满足的边界条件见文献[3]。

在设定库水自由表面、坝体上游坝面、无限远及库底边界条件后，采用Galerkin法对式（2）进行离散，可得到库水的动力平衡方程：式中：Mp、Cp、Kp分别为库水的质量、阻尼和刚度矩阵；Pe为节点压力向量；Rp为坝库交界面上的耦合矩阵；u为节点加速度向量。

坝体的平衡方程：式中：Ms、Cs、Ks分别为坝体的质量、阻尼和刚度矩阵；u为流体的位移向量；f为坝体一库水交界面上荷载向量以外的其他外界激励。

由式（3）、式（4）可得出坝体一库水相互作用的流固耦合方程：

2 有限元模型计算实例与地震波选取

2.1 计算实例

某电站挡水坝段坝顶高程为269.5m，坝底高程为178.0m，正常蓄水位为263.5m，坝顶宽10.0m，坝底宽64.5m。为分析比较不同库水模型下坝体—库水—地基耦合系统的动力特性，分别建立以下4种有限元数值模型：传统Westergaard附加质量模型（Ⅰ），折半修减的Westergaard附加质量模型（Ⅱ），考虑库水可压缩性的流固耦合模型（Ⅲ），忽略库水可压缩性的流固耦合模型（Ⅳ）。Westergaard附加质量模型中采用MASS21单元模拟坝面库水的作用，流固耦合模型中采用Fluid29来模拟库水单元。根据黄耀英等的结论，库水面长度向上游取3倍坝高，计算中忽略库水表面重力波的影响。坝体混凝土静弹性模量为20.60GPa，泊松比取0.167，密度为2400kg/m3；基岩弹性模量为22.50GPa，泊松比取0.25：库水可压缩时体积模量为2.07GPa，密度为1000kg/m3。Rayleigh阻尼因数根据结构前2阶频率计算。采用无质量地基输入模型，根据《水电工程水工建筑物抗震设计规范》，动弹性模量可较静弹性模量提高50%。坝体底部采用全约束，地基四周采用法向链杆约束。

2.2 地震波的选取

计算时，考虑水平向和竖直向的地震动作用，水平向抗震设计地震加速度峰值为0.13g。依据《水电工程水工建筑物抗震设计规范》设计反应谱人工合成地震波。图1为人工合成顺河向地震加速度时程曲线，竖直向地震加速度峰值取水平向的2/3。

3 计算结果及分析

3.1 坝体自振频率

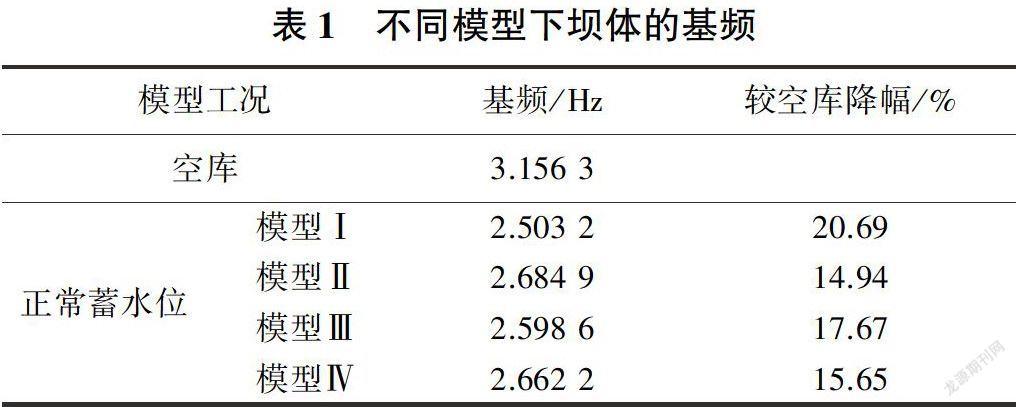
表1给出了坝体空库与正常蓄水位下4种不同库水有限元模型的坝体白振频率。由表1可知，无论哪种库水有限元模型，库水对坝体基频的影响都比较显著，坝体与库水的相互作用使得坝体的白振频率均不同程度降低。空库时坝体基频最高，Westergaard附加质量模型降幅最大，接近21%；Westergaard附加质量折半修减模型对坝体基频的影响较模型Ⅰ有一定程度降低。考虑库水可压缩性时坝体基频略低于不考虑库水可压缩性的情况。

为更直观地比较库水可压缩性对坝体自振频率的影响，绘制了空库、模型Ⅲ和模型Ⅳ的前5阶坝体白振频率分布图，见图2。从图2可以看出，考虑库水可压缩性时，坝体前5阶频率较空库时下降17%～49%，而忽略水体的压缩性时，坝体前5阶频率下降IO%～36%。表明库水可压缩性对坝体自振特性的影响比较显著。因此，考虑库水可压缩的坝体一库水流固耦合有限元模型可更好地反映坝体与库水之间的相互作用。

3.2 不同库水模型对坝体位移的影响

圖3为正常蓄水位时不同库水有限元模型坝体顶部节点和坝体中部节点的顺河向峰值位移对比柱状图。可以看出：地震作用下坝体顶部的放大作用使得其顶部地震动位移较大，坝体中部位移略小。其中：考虑库水可压缩时的模型Ⅲ得到的坝顶节点顺河向峰值位移最大，为1.99Cm；采用传统Westergaard附加质量的模型Ⅰ得到的坝顶节点顺河向峰值位移为1.83cm，相对模型Ⅲ的降幅为8.04%。原因是传统附加质量模型模拟结果是基于刚性坝体假设条件得到的近似解，是将库水的作用简化为附加质量点施加在上游坝面上，这种模型忽略了坝面各节点之间的相互作用，即坝面节点的等效荷载不仅与该节点的库水质量有关系，而且与该节点周围的附加质量有关系，由此可以看出流固耦合有限元模型比传统附加质量模型更能体现出库水对坝体动力特性的影响。

3.3 不同库水模型对坝体应力的影响

表2为不同库水模型对坝体关键部位峰值应力的模拟结果。由表2可知：坝踵节点的主拉应力大于坝体上游折坡处拉应力。模型Ⅰ计算得到的坝踵节点最大主拉应力为3.138MPa，大于另外3种有限元模型的计算结果：考虑库水可压缩条件下的流固耦合库水模型Ⅲ计算得到的坝踵最大主拉应力为2.649MPa；在上游坝面折坡位置，模型Ⅲ最大拉应力相对模型Ⅰ降低13.26%，经折半修减后的模型Ⅱ与忽略库水压缩性的模型Ⅳ计算结果较为相近。可见附加质量模型夸大了库水对坝体的作用，相对坝体中上部来说，在坝踵部位的影响更大。基于流体单元建立库水有限元计算模型时，忽略库水压缩性的模型Ⅳ计算得到的坝体关键部位主拉应力大于可压缩库水模型Ⅲ的计算结果。因此，就传统Westergaard附加质量模型来讲，采用流固耦合模型来模拟坝体一库水之间相互作用更为合理。在坝踵位置考虑库水压缩性较忽略库水可压缩性时主拉应力降低约5%，可知上游库水的压缩性对坝体的应力分布有一定影响。

3.4 不同库水模型对坝面动水压力的影响

图4为不同库水模型对坝面动水压力的影响分布图。从图4可以看出：由传统Westergaard附加质量模型计算所得的动水压力明显大于流固耦合模型计算结果。模型Ⅰ和模型Ⅱ上游坝面最大动水压力分别为241.32kPa和223.65kPa，最大值出现的位置在坝高62m处，约为坝高的2/3。采用流固耦合模型计算时，考虑库水可压缩情况下的模型Ⅲ上游坝面动水最大压力为145.68kPa，相对模型Ⅰ和模型Ⅱ分别降低39.6%和34.9%。采用Westergaard附加质量模型计算所得的动水压力，上部明显偏大，而下部明显偏小，原因是在地震作用下坝体加速度随坝高增大放大作用增大，导致Westergaard模型计算结果被明显夸大，与实际动水压力分布不吻合，采用流固耦合算法所得的结果更为合理，这与文献试验得到的结论吻合。

4 结论

从坝体一库水相互作用的物理特性来看，可压缩库水模型可以更好地反映库水对坝体动力特性的影响。不同库水模型对结构的白振频率和振型的影响较为显著，Westergaard附加质量模型在一定程度上夸大了水体的作用：可压缩与不可压缩水体相比降低了坝体的白振频率，且下降幅度要大于不可压缩库水模型的，在计算中不应忽略。

数值算例表明：库水可压缩情况下坝体顶部节点和坝体中部节点峰值位移要大于采用Westergaard附加质量模型的计算结果：对不同模型得到的主拉应力进行分析可知，采用Westergaard附加质量模型计算得到的结果偏大。虽在文中对Westergaard附加质量模型进行了折半修减处理，但具有不确定性。

对比流固耦合模型与附加质量模型计算所得的坝面动水压力，可知采用流固耦合模型模拟坝体一库水的相互作用更为合理。

本文结论是在忽略库水表面重力波效应及未计入库底淤沙层对地震波的吸收作用等的前提下得到的，而坝体一库水一地基系统的耦合作用非常复杂，因此还有待深入研究。