平底突扩断面水跃共轭水深分析计算

高远 张根广 吴彰松 李林林 杨耀天

摘要：基于平底突扩水跃形成机制，认为突扩断面回流区平均水深取决于突扩断面上游渠道的能量水头及断面突扩比等。假定突扩断面回流区平均水深等于突扩断面上游渠道能量水头乘以修正系数，通过实测资料分析，建立了修正系数与上游渠道弗劳德数以及断面突扩比的关系式，并将突扩断面回流区平均水深代入平底突扩水跃共轭水深一般方程，得到了跃后水深计算公式。经实测资料验证，本文跃后水深计算公式计算结果与实测资料符合良好，误差较小。

关键词：突扩水跃；突扩断面；回流区平均水深；共轭水深比

中图分类号：TV135.2+1

文献标志码：A

doi：10.3969/j.issn.1000-1379.2018.08.030

水流由急流过渡到缓流水面会突然跃起形成水跃。在水跃区，水流强烈紊动、混掺，水力要素急剧变化。突扩水跃是水流从较窄断面渠道进人较宽断面渠道时突然扩散形成的一种复杂空间流态，是平原地区闸下出流的一种常见形式。NallamuthuR.等将突扩水跃分为远驱水跃（又称R水跃）和稳定水跃（又称S水跃）两种。R水跃跃首位于突扩口下游宽渠道中，跃首至突扩口存在一段急流，流态不稳定：S水跃跃首位于突扩口，类似于淹没水跃，流态稳定。S水跃在突扩断面后形成回流区，又称为空间水跃。陈朝等研究表明，回流旋涡区与主流之间形成强烈的紊动剪切层，增加了能量的耗散：陈文鑫等研究表明，突扩水跃较典型水跃消能效果明显提高，可有效降低消力池边墙水力学指标。此外，作为一种新型消能工——跌扩型底流消能工拟在一些大型水利工程中应用。

1 跃前水深与跃后水深关系建立

工程上常采用一定淹没度的水跃消能。共轭水深比是研究水跃的基础，也是工程上进行消力池设计的重要依据。水跃跃前水深与跃后水深之间的关系通常由恒定总流动量方程推求。在推导过程中假定：①明渠水跃长度较短，明渠边界对水流摩擦力可忽略不计；②跃前、跃后过水断面上动水压强符合渐变流规律，即压强按静水压强计算；③跃前、跃后断面上动量校正系数相等，令β1β2=β（β1、β2为跃前、跃后动量修正系数）。

依据上述假定，建立断面1-1、2-2（见图1，其中：P1为跃前断面静水压力；P2为跃后断面静水压力：P3为突扩断面边墙水压力）间水体动量方程：式中：p为流体密度；Q为流体流量；v1为跃前断面流速：v2为跃后断面流速；g为重力加速度：b为跃前断面宽度；B为跃后断面宽度：h1为跃前断面水深：h2为跃后断面水深；h3为突扩断面回流区平均水深。

显然，求解式（1），在联立水流连续方程Q=bh1v1=Bh2v2，基础上，还需要知道回流区平均水深h3。为求解h3，许多学者采取了不同的假定。

汪涛等在上述3个假定的基础上引入h3=h1，β1=β2=1.0，通过对式（1）进行无因次数学变换，得到跌扩共轭水深理论公式，并将其进一步演变为突扩型水跃共轭水深理论公式：式中：突扩比ζ=B/b；共轭水深比η=h2/h1；跃前弗劳德数Fr1=v1/√gh1。

卢士强等通过试验观测认为，近主流侧（内侧）水深与h1值接近，远主流侧（外侧）水深则稍高一些，并假定h3=0.5（h1+h2），进而得到

卢士强通过对文献中的试验数据进行多元非线性拟合，得到工程设计参考经验公式：

Hager w.H.通过假定h2/3=1/2（h21+h22），得到

2 回流区平均水深h3的确定

2.1 h3的影响因素及假定

Nallamuthu R.等通过对S水跃的研究得到，突扩口淹没水深与出口特征长度的弗劳德数有关，且出口特性长度最小值为上游水深的2倍。故可推定，突扩口淹没水深与上游弗劳德数有关。卢士强等在研究突扩水跃共轭水深时指出，远主流侧水深与Fr1等有关。程天金等在研究单边突扩浅水回流时得到，回流长度随进口断面弗劳德数Fr1增大而增大，同时具有随水深h1增大而增大的趋势。可见，回流长度是衡量回流强度的一个重要指标，而回流强度直接影响边墙时均动水压强及回流流速分布。因此，边墙时均动水压强受断面弗劳德数Fr1、上游水深影响。

综上分析，突扩口回流区强度、范围、平均水深h3与上游渠道水流弗劳德数Fr1及断面水深h1有关。弗劳德数的物理意义为过水断面单位质量液体平均动能与平均势能之比的二倍开平方，具有能量比的概念，因此h3与上游断面水流弗劳德数或单位质量液体能量有关。而式（2）～式（5）中假定的回流区平均水深h3都没有包含上游渠道水流弗劳德数Fr1或能量等参数，为此，作者假定突扩口边墙回流区平均水深h3等于上游过水断面单位能量乘以一系数，即式中：K为待定系数。

2.2 修正系数K的确定

根据式（6）可得修正系数K表达式为

分析文献[1]试验实测资料可知，在确定的h1、h3条件下，系数K与Fr1和ζ均呈复杂的幂函数关系，且K与（ζ-1）-0'2Fr21的拟合关系较好。根据文献[1]试验实测资料对K值进行拟合，见表1、图2。

由表1及图2可得

3 共轭水深比η与跃后断面水深h2求解

将式（7）整理成迭代式：

将式（9）代人式（10）进行迭代求解，即可求得η值。Nallamuthu R.等根据试验成果得出回流区水深约是跃前水深的4倍，因此建议式（10）的迭代初始值η1=4。跃后断面水深为

4 公式验证

根据文献[1]中S水跃试验资料及文献[9]中ζ=1.2、1.5、2.0、3.0四种T况试验数据，取β1=β2=1.o；对式（2）～式（5）及本文公式（10）进行对比分析。

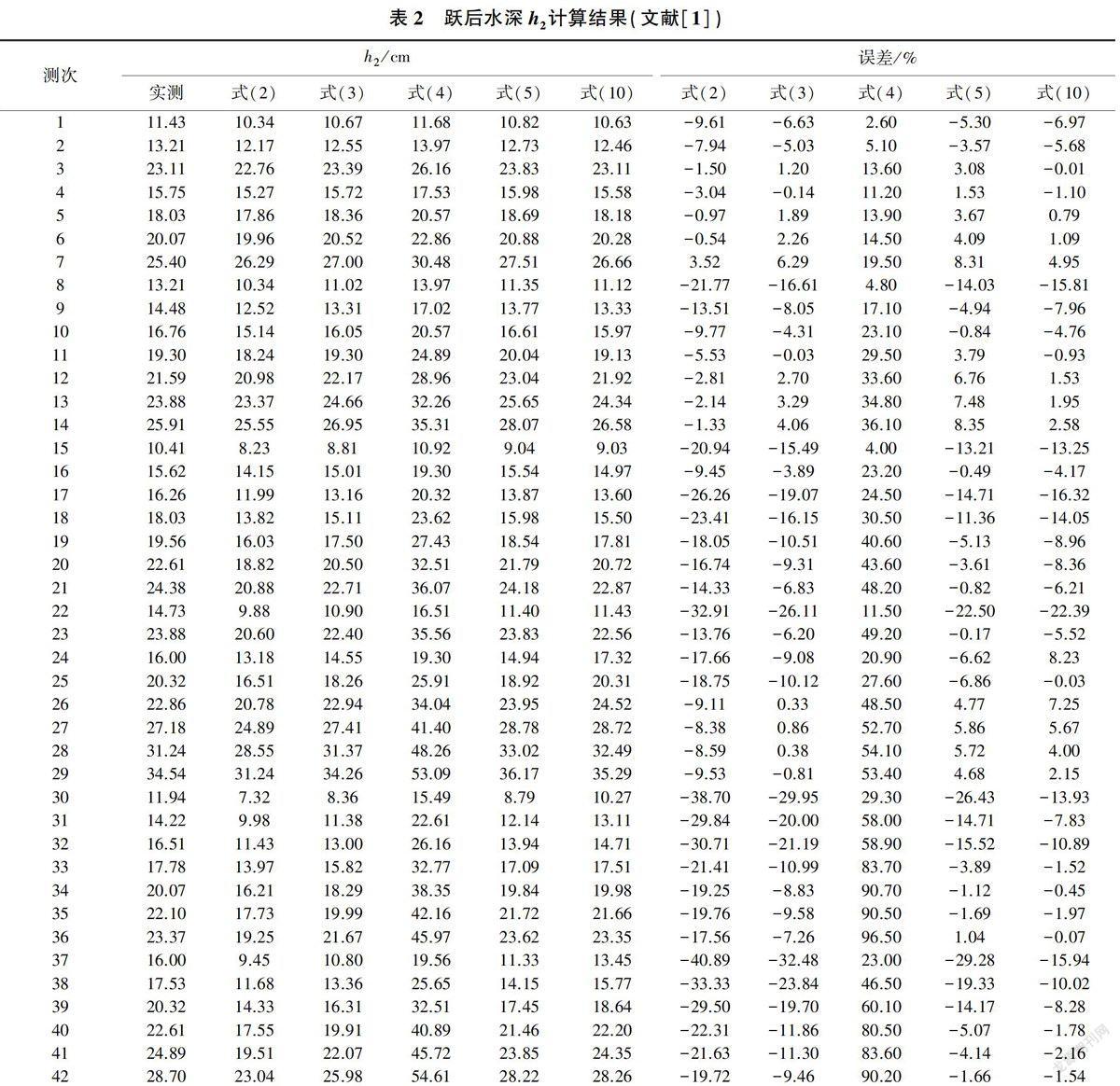
（1）文献[1]中s水跃试验资料公式验证。由式（2）～式（5）及本文公式（10）求得共轭水深比η，代人式（11）计算得出h2，对比不同方法计算结果的准确度，见表2（跃前断面宽度b、突扩比ε、跃前弗劳德数Fr1、实测h1数据见表1：表中h2，计算值取2位小数：误差为“-”表示计算值小于实测值）。由表2可知，式（2）计算结果的平均误差为16.11%，最大误差为40.89%，42测次计算值中有41次小于实测值；式（3）计算结果的平均误差为9.86%，最大误差为32.48%，有32测次的计算跃后水深小于实测水深：式（4）计算结果的平均误差为40.08%，最大误差为96.50%，所有计算结果均大于实测水深；式（5）计算结果的平均误差为7.63%，最大误差为29.28%，28测次的计算值小于实测值：本文公式（10）的计算结果的平均误差为6.17%，最大误差为22.39%，31测次的计算值小于实测值。可见，本文公式计算精确度优于其他几个公式的，说明本文假定更合理。

（2）文献[9]中ε=1.2、I.5、2.0、3.0四种工况公式验证。由表3（表中h2计算结果取2位小数）可知，式（2）计算结果的平均误差为6.75%，最大误差为21.50%，40次计算有37次计算值小于实测值：式（3）计算结果的平均误差为3.08%，最大误差为10.99%，有13次计算值小于实测值；式（4）计算结果的平均误差为49.53%，最大误差为103.6%，所有的计算值均大于实测值；式（5）计算结果的平均误差为5.78%，最大误差为11.76%，有3次计算值小于实测值：本文公式计算结果的平均误差为5.48%，最大误差为25.93%，有9次计算值小于实测值。可知，本文公式计算結果的精确度仅次于公式（3）。

5 结论

通过分析研究平底突扩式水跃的形成机制，认为突扩断面回流区平均水深取决于突扩断面上游渠道的能量水头及断面突扩比等。假定突扩断面回流区平均水深等于突扩断面上游渠道能量水头乘以修正系数，通过进一步分析，建立了修正系数与突扩断面上游渠道弗劳德数及断面突扩比的关系式，并将突扩断面回流区平均水深代人平底突扩水跃共轭水深一般方程，得到了跃后水深的计算公式。实测资料验证表明：本文跃后水深计算公式计算结果与实测资料符合良好，与实测数据相比误差较小，说明本文假定合理。