“爱上网”的旋转变换
仲崇辉
在中考试题中,图形的旋转问题比较多,而且形式多样,特别是以网格为载体的旋转问题,在每年的各地中考中比比皆是。
例1 (2017年泰安卷)如图1,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为( )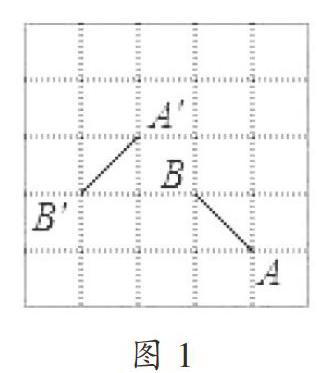
A.30° B.60°
C.90° D.120°
分析 根据题意确定旋转中心后即可确定旋转角的大小。
解 如图2,显然,旋转角为90°,故选C。
点评 标题考查了旋转的性质,解题的关键是能够根据题意确定旋转中心,知识难度不大。
例2 (2017年威海卷)如图3,A点的坐标为(-1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐标为(3,-1),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是 。
分析 分点A的对应点为C或D两种情况考虑:①当点A的对应点为点C时,连接AC、BD,分別作线段AC、BD的垂直平分线交于点E,点E即为旋转中心;②当点A的对应点为点D时,连接AD、BC,分别作线段AD、BC的垂直平分线交于点M,点M即为旋转中心。此题得解。
解 ①当点A的对应点为点C时,连接AC、BD,分别作线段AC、BD的垂直平分线交于点E,如图4所示。
∵ A点的坐标为(-1,5),B点的坐标为(3,3),
∴ E点的坐标为(1,1)。
②当点A的对应点为点D时,连接AD、BC,分别作线段AD、BC的垂直平分线交于点M,如图5所示。
∵ A点的坐标为(-1,5), B点的坐标为(3,3),
∴ M点的坐标为(4,4)。
综上所述:这个旋转中心的坐标为(1,1)或(4,4)。
故答案为:(1,1)或(4,4)。
点评 本题考查了坐标与图形变化中的旋转,根据给定点的坐标找出旋转中心的坐标是解题的关键。
例3 (2017年福建卷)如图6,网格纸上正方形小格的边长为1。图中线段AB和点P绕着同一个点做相同的旋转,分别得到线段和点A′B′,则点P′所在的单位正方形区域是( )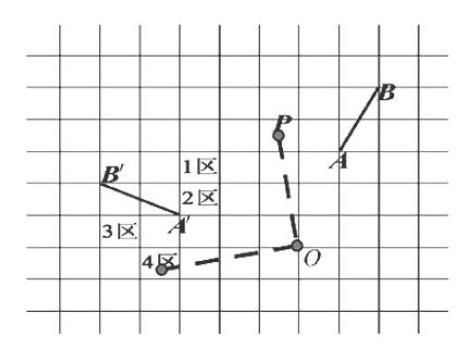
A.1区 B.2区
C.3区 D.4区
解析 如下图,根据题意可得旋转中心O,旋转角是90°,旋转方向为逆时针,因此可知点P的对应点落在了4区。故选D。
点评 本题主要考查图形的旋转,能根据题意正确地确定旋转中心、旋转方向、旋转角是解题的关键。
例4 (2016年攀枝花卷)如图7,在平面直角坐标系中,直角△ABC的三个顶点分别是A(-3,1),B(0,3),C(0,1)。
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)分别连结AB1、BA1后,求四边形AB1A1B的面积。
分析 (1)利用网格特点,延长AC到A1使A1C=AC,延长BC到B1使B1C=BC,C点的对应点C1与C点重合,则△A1B1C1满足条件。
(2)四边形AB1A1B的对角线互相垂直平分,则四边形AB1A1B为菱形,然后利用菱形的面积公式计算即可。
解 (1)如图8,△A1B1C1为所作。
(2)四边形AB1A1B的面积=×6×4=12。
点评 本题考查了作图-旋转变换。根据旋转的性质可知,对应角都相等,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形。
例5 (2017年宁夏卷)如图9,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(2,3),B(1,1),C(5,1)。
(1)把△ABC平移后,其中点A移到点A1(4,5),画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,画出旋转后的△A2B2C2。
分析 (1)根据图形平移的性质画出平移后得的△A1B1C1即可。
(2)根据图形旋转的性质画出旋转后的△A2B2C2即可。
解 (1)如图10,△A1B1C1即为所求。
(2)如图,△A2B2C2即为所求。
点评 本题考查的是作图-旋转变换,熟知图形旋转不变性的性质是解答此题的关键。
(编辑 孙世奇)

