基于梯度风假设的新台风风场模型

申赵勇，金 生

(大连理工大学建设工程学部，辽宁 大连 116024)

台风是一种发生在热带海洋上的强烈风暴，其在海上发展，会引起沿海地区的潮位增加，给人类和社会带来严重的灾害[1]，而台风气压场风场是影响风暴潮数值计算精度的关键因素[2]。目前，气压场的数学模型主要有三类：理论气压模型等圆对称气压场模型；经验模型；半经验半理论模型[3]。台风风场的数学模型主要有两类：动力理论；经验风场模型[4]。现阶段对台风风场的模拟中，有很多学者是将风场分为两部分来考虑[5- 8]，其中一部分是基于梯度风假设，即假设气压梯度、科里奥利力和离心力三者受力平衡下推导出的台风中心不移动的对称风场(简称梯度风风场)，另一部分是考虑台风的移动对最终风场的影响(简称为移型风风场)。本文基于动力理论，提出了一种新的气压场风场模型，并通过C#语言编程构造了其数值模型。

1 台风风场模型

本文将风场分为两部分来考虑，即梯度风风场、移型风风场。

1.1 梯度风风场

根据梯度风假设，即假设气压梯度力、科里奥利力和离心力三者受力平衡，有：

F1+F2+F3=0

(1)

式中，F1—气压梯度力；F2—科里奥利力；F3—离心力，分别有：

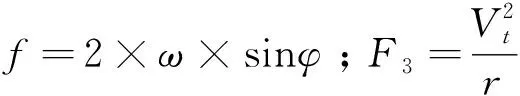
式中，ρ—气体密度；p—压强；f—科氏力系数；Vt—台风梯度风风速；ω—地球自转角速度；φ—所在纬度；r—计算点距中心的距离。故而整理如下：

(2)

将式(2)求解可得：

(3)

由上可知，梯度风风速很大程度上取决于压强场数值模型，故本文提出了一种新的压强场模型，如下：

(4)

式中，

(5)

(6)

式中，Δp=p∞-pc，p∞—环境气压值；pc—中心气压值。

1.2 移型风风场

现阶段主要是基于经验公式[5]，理论方面比较欠缺，并且主要是考虑位置点到中心的距离r和最大风速半径的影响。本文提出的移型风风场模型中，将梯度风风场的因素考虑在内，形成了如下所示的移型风风场模型。

(7)

(8)

1.3 合成风场

考虑到气压梯度与风场之间有个约20°的夹角[6]，如图1所示，所以梯度风风速的x和y方向的分向速度表示如下：

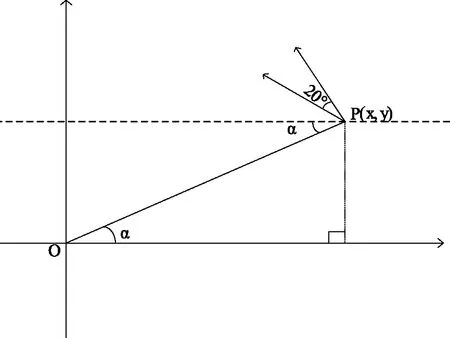
图1 风场与等压线之间的关系图

(9)

(10)

结合图1可知：

(11)

(12)

因此，最终将梯度风风场和移型风风场线性叠加可得最终的台风风场为：

(13)

(14)

2 模型应用与验证

将提出的模型分别应用于台风Damrey(1210)、Krovanh(0312)和Matsa(0509)的模拟中，其中台风数据来源于台风路径数据(tcdata.typhoon.gov.cn)[15]。最大风速半径方面，罗哲贤学者曾表示，在实时预报时，最大风速半径取常数值70km[9]，所以本文中拟取最大风速半径为70km。计算域方面，本文均选取以台风为中心，半径为500km的圆形区域来逐时模拟。网格划分时采用的局部坐标系为平面极坐标系，网格间距拟设置为：Δθ=10°，Δr=5km。

在展示模拟结果的过程中，本文分别选取四个时间点的气压场、风场模拟结果，将结果输出到Tecplot软件中进行展示。在验证模型结果的过程中，本文选取了现阶段在计算风暴潮的过程中，常见的两种风场模式，即王喜年学者常用的风场模式[10- 14]和阎秉耀学者常用的风场模式[5，10]，通过C#语言编程构造其数值模型，采用相同的数据，对三次台风进行分别模拟计算，并进行结果的对比。

2.1 Damrey台风的模拟结果

2.1.1 气压场模拟结果

将本文提出的气压场模型计算的Damrey台风气压场数据中第66h、108h、150h和192h结果通过Tecplot展示如图2所示：

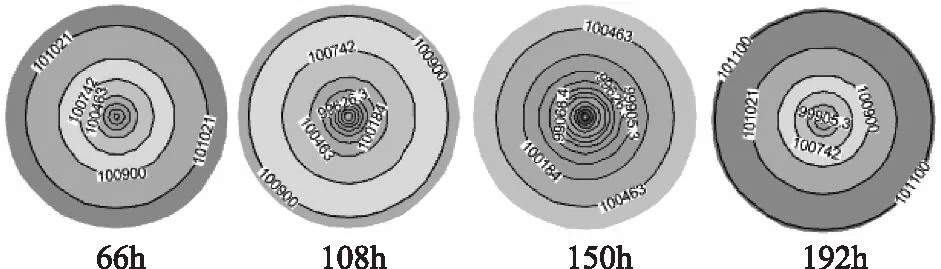
图2 气压场的逐时变化

在第150h，台风出现最低气压值，三类气压场模式下，气压随距离的变化规律如图3所示。

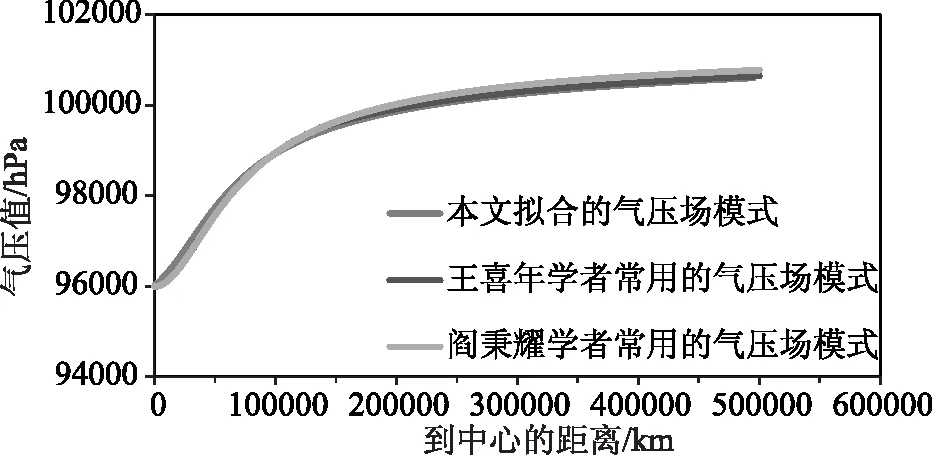
图3 气压随距离的变化过程

2.1.2 风场模拟结果

第66h、108h、150h和192h风场的逐时展示如图4所示，由本文提出的风场模型计算的结果通过Tecplot展示如下:

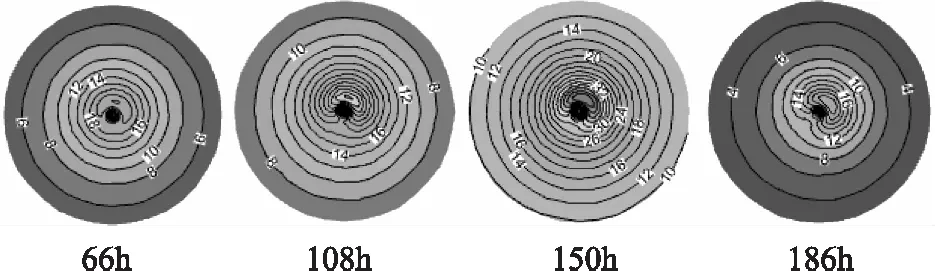
图4 风场的逐时展示

在出现最低气压值的时候，三类风场模式计算的风速随距离变化规律如图5所示。

图5 风速随距离的变化规律

在Damrey台风的整个移动过程中，三类风场模式计算的最大风速值随时间的变化规律如图6所示。

图6 最大风速随时间的变化规律

2.2 Krovanh台风

2.2.1 气压场模拟结果

台风Krovanh(0312)由本文提出的气压场模型计算的第66h、126h、186h和246h气压场结果由Tecplot展示如图7所示。

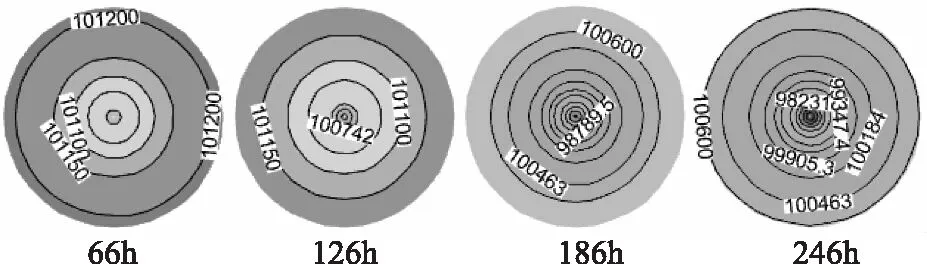
图7 气压场的逐时展示

台风Krovanh(0312)在第246h出现最低气压值，下图为三类气压场模式下，气压随距离的变化规律如图8所示。

图8 气压随距离的变化规律

2.2.2 风场模拟结果

台风Krovanh(0312)在本文提出的风场模型的计算下，第66h、126h、186h和246h风场结果由Tecplot展示如图9所示。

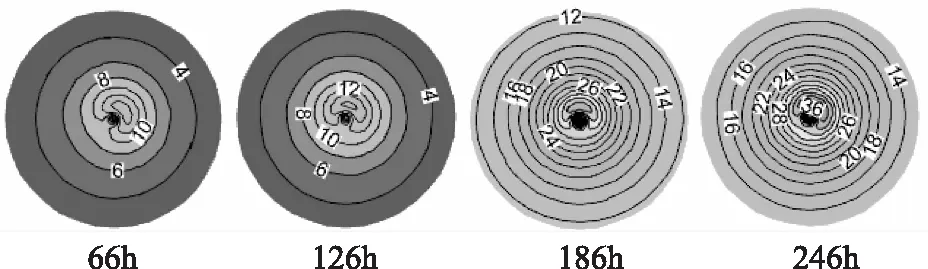
图9 风场的逐时展示

台风Krovanh在第246h出现最低气压，此时三类风场模式计算的风速随距离的变化过程如图10所示。

图10 风场随距离的变化规律

在台风Krovanh的整个移动过程中，经过三类风场模型的计算后，最大风速随时间的变化过程如图11所示。

图11 最大风速随时间的变化规律

2.3 Matsa台风

2.3.1 气压场模拟结果

对于台风Matsa(0509)，使用本文提出的气压场模型来模拟时，其第72h、126h、180h和234h气压场模拟结果如图12所示。

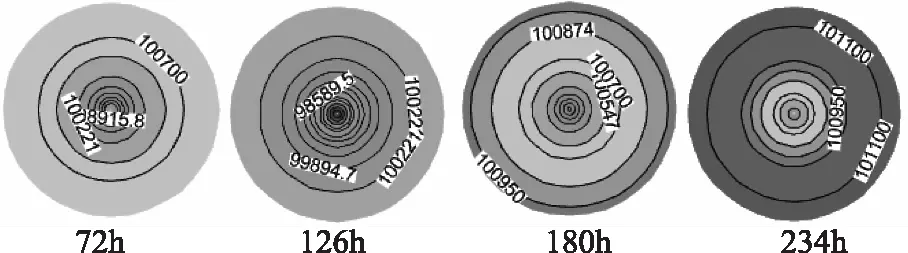
图12 气压场的逐时展示

第126h台风Matsa出现最低气压，此时三类气压场模型计算所得的，气压随距离的变化过程如图13所示。

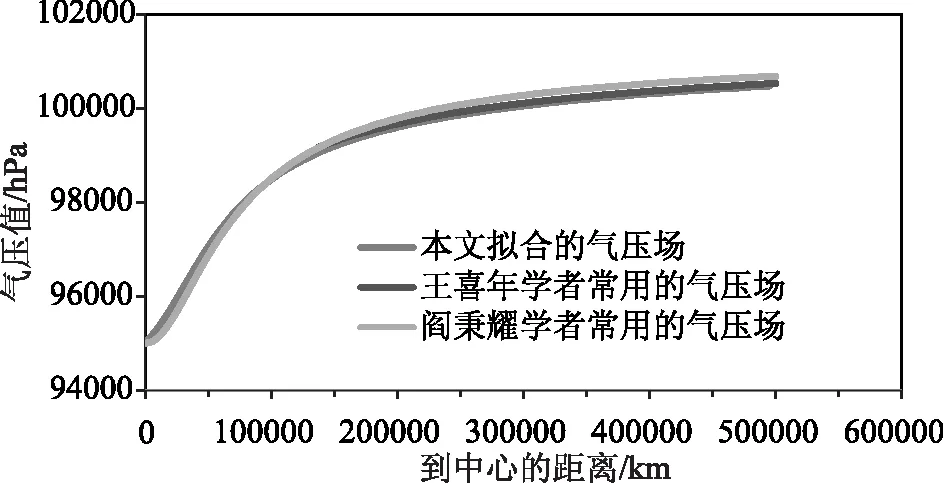
图13 气压随距离的变化规律

2.3.2 风场模拟结果

本文提出的风场模型计算所得的，台风Matsa(0509)在第72、126、180和234h风场数据通过Tecplot展示如图14所示。

图14 风场的逐时展示

第126h台风Matsa出现最低气压，此时三类气压场所计算的风速随距离的变化过程如图15所示。

图15 风场随距离的变化规律

在台风Matsa的整个移动过程中，三类风场模式计算的最大风速值随时间的变化如图16所示。

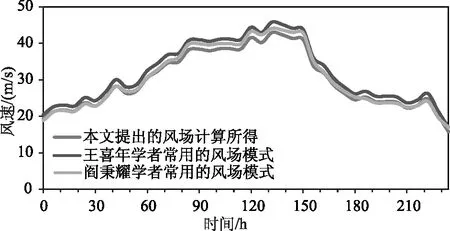
图16 最大风速随时间的变化规律

2.4 结果分析

由图2、7和12可分别看出，台风Damrey、Krovanh和Matsa气压场在最大风速半径内，快速的增大，变化速率明显大于最大风速半径外，符合目前对台风气压场的认识规律；由图4、9和14可分别看出，台风Damrey、Krovanh和Matsa风场的最大风速出现在，与其移动方向成顺时针90°+β的位置处，其中表示一个角度，且β∈(0，├π/2┤。由图3、5、6、8、10、11、13、15、16可看出，本文提出的气压场、风场模型计算结果与两位学者常用的模型所计算的结果相比，最大的差额亦在5%之内，由此可说明，本文提出的模型对Damrey、Krovanh和Matsa台风具有很好的模拟效果。与此同时，在选择模拟具体台风时，随机选择的Damrey、Krovanh和Matsa，故而认为本文提出的气压场风场模型具有普遍适用性。

3 结论

(1)本文提出的气压场模型公式与文中提及的气压场公式相比，提高了风场中心的气压变化率。

(2)对于气压场公式，在2倍于最大风速半径外，本文提出的气压场公式和王喜年学者采用的气压场公式模拟效果基本相同，数值相差不到5‰。

(3)对于移型风风场的考虑，加进了梯度风风场的影响因素，使得整个风场模型不再是两个完全不相关的因数的叠加，增加了整个风场模型的整体性。