基于逆向地应力转换的煤系储层压裂层段弹性参数取值分析

张宝录,曾蕊,杜欣睿,吴思薇,苟焌迤

(中国石油测井有限公司长庆分公司,陕西 西安 710200)

0 引 言

现今地应力评价可以为油气成藏、储层压裂改造及水平井井网优化等方面研究提供技术支撑,该参数是油气田勘探开发过程中的重要评价内容[1-2]。利用高分辨率测井资料对储层现今地应力进行评价可以获得储层地应力在纵向上的连续分布[3]。常用的现今地应力测井解释模型主要包含莫尔-库伦准则模型、单轴应变模型及地层各向异性模型3类[4]。莫尔-库伦准则模型仅适用于地质结构较为松软的泥(页)岩地层;单轴应变模型则由于没能考虑地应力在水平方向的各向异性,因此,仅适用于构造活动较弱的盆地腹部区域;相对而言,地层各向异性模型则较好地克服了前述2类模型的不足,适用于强非均质性致密储层,具有最为广阔的应用空间[3]。在应用地层各向异性模型(如Terzaghi模型、Anderson模型、Newberry模型及黄氏模型)时[2-4],通常要用到岩石的泊松比、弹性模量等弹性参数。地应力的产生实质上是由岩体的变形诱发的,岩石泊松比及弹性模量能够较好反映岩石应力-应变特性的理想参数[3-4]。因此,这些静态弹性参数取值的合理与否,会直接关系到现今地应力场的预测精度。

小型水力压裂测试和差应变实验测试均能准确地测定地层的现今地应力大小,它们也是进行地应力测井解释中所需的最为可靠的实测结果[5]。对于压裂测试来说,通常无法获取压裂层段的岩心并进行岩石力学实验,所以无法获取地层的弹性参数。此时,通常采用动静态弹性参数转换的方法间接获取地层岩石的弹性参数,从而进行地应力测井评价。因此,利用动静态参数转换所获得的压裂层段岩石的静态弹性参数是否合理关系到所解释的地应力结果是否可靠[6]是一个值得探讨的问题。因此,有必要对压裂层段弹性参数取值问题进行深入分析。研究区位于鄂尔多斯盆地东北缘临兴-神府地区,该地区上古生界发育多套煤系致密砂岩气藏[6]。区内致密气开发所面临的主要问题为储层强非均质性所造成的储层改造效果差及单井产能差异大,因此,迫切需要对该地区煤系现今地应力进行合理评价,同时,应尽可能提高预测精度,从而为压裂及井网设计提供依据。本文基于逆向转换分析思路,利用压裂法确定煤系储层地应力大小,在考虑岩石热膨胀系数(β)基础上,利用现今地应力校正致密砂岩储层弹性参数(包括弹性模量及泊松比),同时,与常规动静态参数转换模型结果进行了对比。研究结果对指导强非均质性非常规致密储层现今地应力场综合评价具有指导意义。

1 研究区概况

研究区位于鄂尔多斯盆地东北缘临兴-神府地区,其构造位置位于鄂尔多斯盆地伊陕斜坡和晋西挠摺带上,地势呈东高西低、北高南低[6]。该地区上古生界发育多套煤系致密砂岩气储层,含气层系多,包括石千峰组5段、盒1段、盒2段、盒3段、盒4段、盒5段、盒6段、盒7段、盒8段、山西组及太原组。目前,该地区上古生界煤系致密气勘探取得了重要进展,区内致密气的探明储量1 585.74×108m3,剩余资源量3 040.37×108m3,反映出该地区的资源潜力巨大,勘探前景好。

2 岩石力学实验及压裂测试

2.1 岩石力学实验

测试样品取自研究区石千峰组、上石盒子组及太原组层位,为致密砂岩储层岩样。对样品进行了三轴力学及声学同步测试,测试仪器为MTS岩石物理测试系统。全套装置由高温高压三轴室、围压加压系统、轴向加压系统、超声波换能器、超声波脉冲发射-接收控制盒及加温恒温系统等主要部分组成。三轴室的设计指标为围压200 MPa,可容纳岩样的直径为50 mm。三轴室的围压及轴压全部由电液伺服控制加压,试验中岩样的轴向、横向应变及轴向载荷由装在高压釜内传感器来测量,数据信号传输到TESTSTAR自动采集控制系统。压力传感器的误差<1%,位移分辨率为0.000 1 mm。

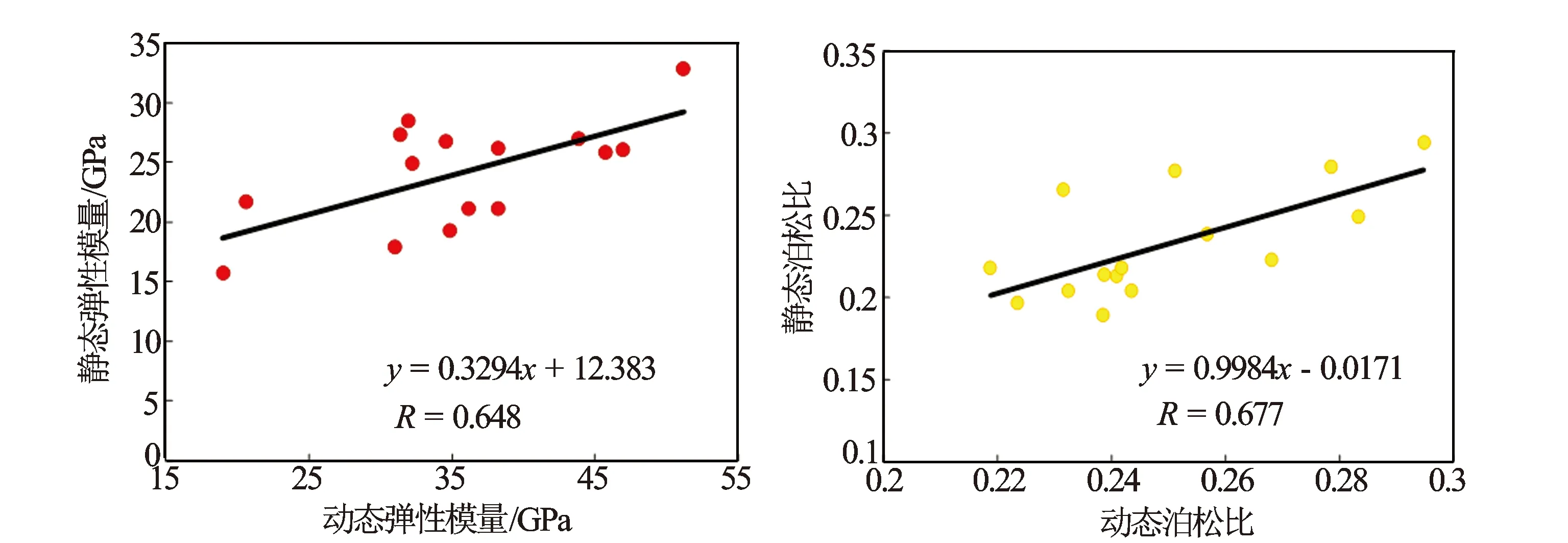
图1 致密砂岩岩样动静态弹性参数转换模型

模拟地层条件下致密砂岩岩样的动静态弹性参数转换关系如图1所示,动态参数物理方程见式(1)和式(2)。从图1可见,致密砂岩岩样的弹性参数均表现为静态值略小于动态值,这与前人的研究结果一致[7]。所测试岩样的动静态弹性模量及泊松比之间均具有较好的正相关关系。

从图2可见,所测试岩样的静态弹性模量及静态泊松比之间也具有非常好的正相关性。这与该地区上古生界煤系致密砂岩储层的压实路径有关,其经历了强烈的压实过程,储层极为致密。相对浅层的脆性岩石,随着弹性模量的增加,其泊松比会出现降低,弹性模量与泊松比之间会呈现出一定负相关性[8]。而对于深层经历了强烈压实演化的致密砂岩储层,其变形具有明显的塑性特征,随着埋深或环境应力的增加,岩石的弹性模量和泊松比均逐渐增加[8]。目的层岩样弹性模量和泊松比之间具有非常好的正线性相关关系,且相关系数较高,表明可以利用泊松比对岩石弹性模量进行定量表征(见图2)。

(1)

(2)

式中,ρ为岩石密度,g/cm3;vP和vS分别为纵波波速和横波波速,m/s;E为弹性模量,GPa;ν为泊松比,无量纲。

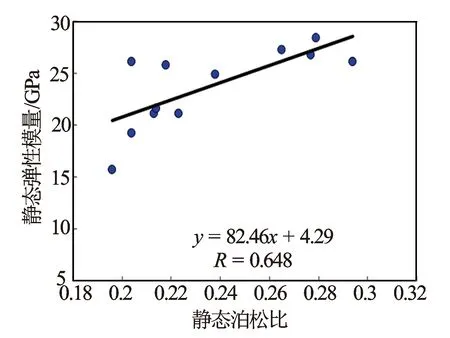
图2 测试岩样静态弹性模量及静态泊松比关系

2.2 压裂测试

只有小型水力压裂测试和差应变实验测试可以准确确定地层岩石的现今地应力大小,其他方法如声发射及井壁破裂反演法等确定的现今地应力均为相对值[9]。小型水力压裂测试由于消除了邻层及岩性变化等因素的影响,应用效果最好。本文采用压裂测试分析方法获取了研究区目的层25个压裂层段的现今地应力数据。随着埋深的增加,3个方向主应力均有逐渐增加的趋势,整体来看,地应力状态基本满足:σh(水平最小主应力)<σH(水平最大主应力)<σv(垂向主应力)。部分数据呈现出σh<σv<σH的应力状态,表明局部地层应力环境复杂,具有较强的构造应力。随着埋深的增加,水平差应力(σH-σh)也具有逐渐增加的趋势。

3 基于逆向地应力转换的岩石弹性参数评价方法

地壳表层是构造活动最为活跃的区域,伴随着伸展、挤压等各种构造活动类型,活动强度明显强于深层。例如岩石圈年水平位移量在0.1～12 cm附近,而上地幔的年水平位移量通常小于2 cm[10]。随埋深变化,岩石的力学性质及应力环境均会发生变化。对于埋深一定的沉积岩体,其水平方向主应力受岩石弹性力学参数及温度梯度的综合控制。此时,岩石水平方向最小主应力(σh)为[11]

(3)

式中,β为热膨胀系数,不同类型岩石具有不同的β值,可通过文献[12-14]查值获取(见表1);G为地温梯度,℃/m;H为埋深,m;E为弹性模量,MPa。

由式(3)可见,地层σh值大小受岩石弹性参数(如E和ν)及温度梯度参数(如β和G)的联合控制。仅从式(3)来看,随着岩石弹性模量和泊松比的增加,岩石的σh值均会出现一定程度增加,符合地壳表层沉积岩体的力学性质及地应力的变化特征,即随着埋深的增加,岩石逐渐由脆性转变为韧性,相应其弹性模量和泊松比均升高,地应力逐渐增加[15]。图2显示,所研究煤系致密砂岩的E和ν具有非常好的正相关性,该致密砂岩的ν值主要分布在0.15～0.35之间。根据图2拟合关系模型,利用弹性模量表征泊松比,并代入式(3),可得

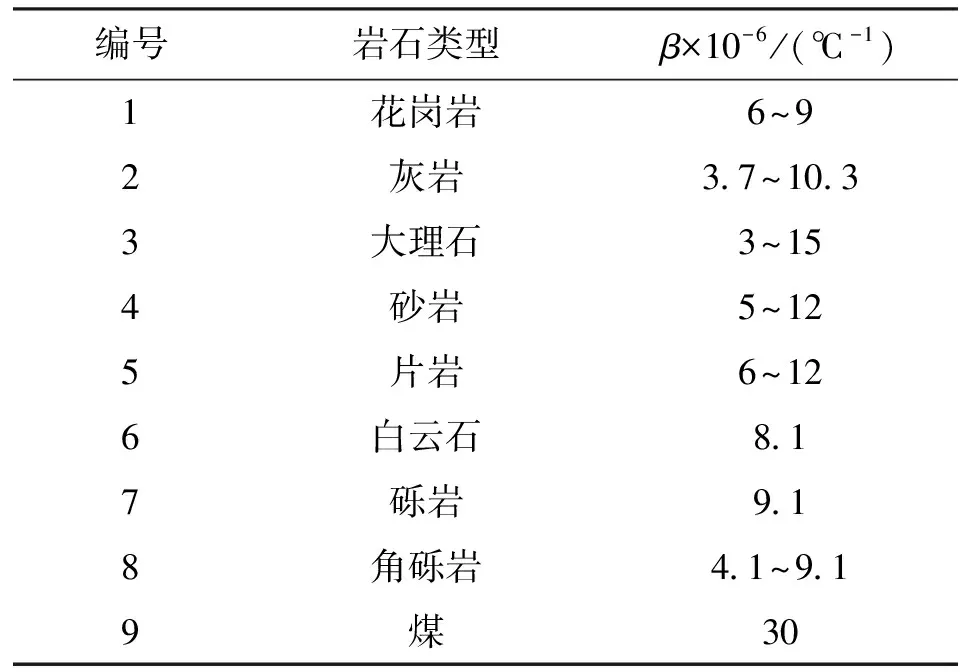
表1 不同岩性岩石热膨胀系数β取值表

(4)

式(4)同时考虑了岩石弹性模量及泊松比对地层水平最小主应力的影响。对于研究区而言,上古生界目地层G取0.025 ℃/m,H取平均值2 000 m,σv的应力梯度取0.026 MPa/m。对于β值,根据表1可知,β值的大小与岩石内部矿物组分及其排列方式等因素有关,砂岩的β值主要分布在(5～12)×10-6/ ℃[12-14]。因此,在该取值范围内对β赋不同值,可建立该地区上古生界煤系地层σh与泊松比(0.15<ν<0.35)间的关系图版(见图3)。

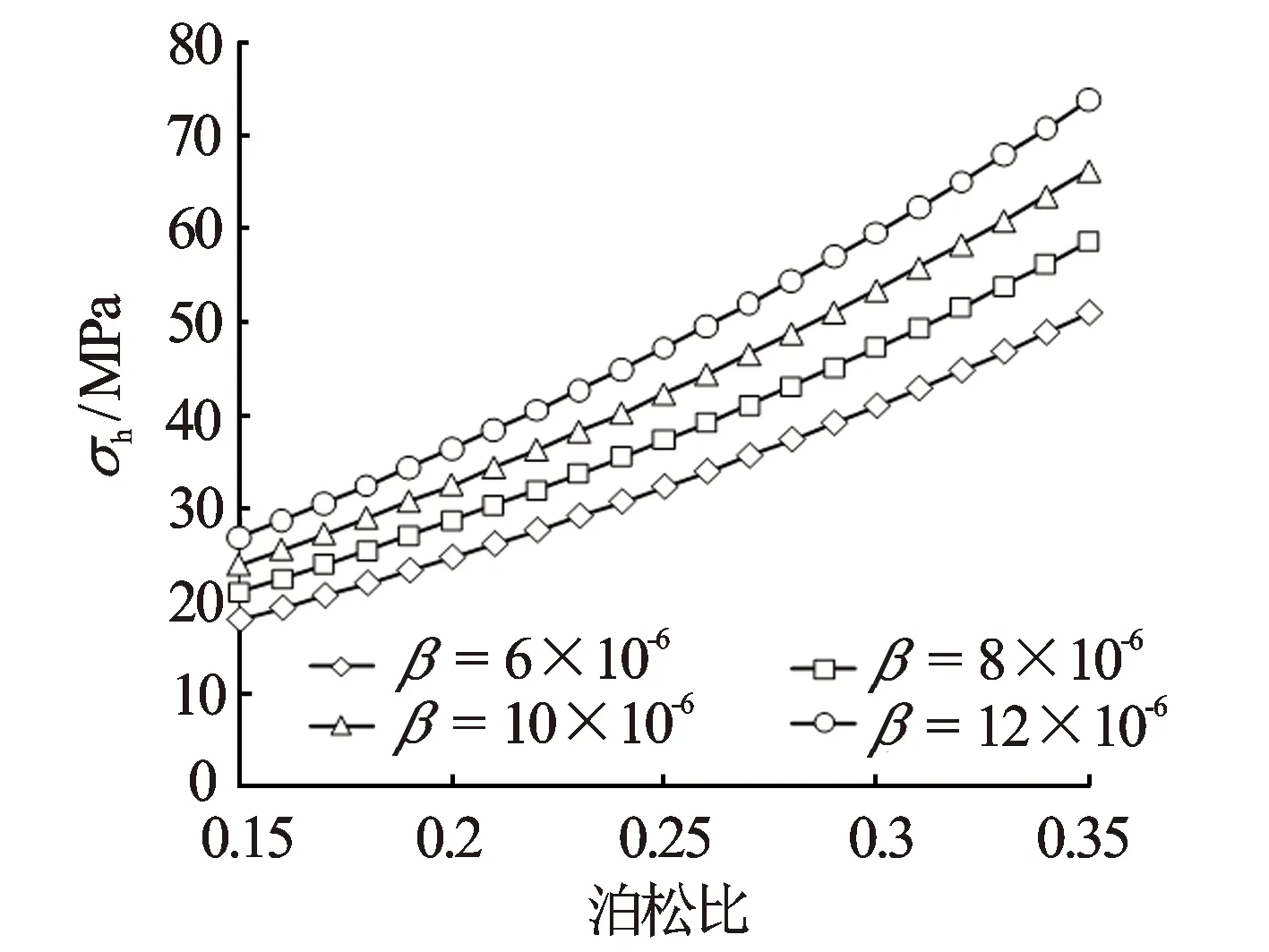
图3 研究区目的层σh与泊松比间的关系图版

由图3可见,对于该地区上古生界煤系地层,随着地层岩石泊松比值的增加,σh值逐渐升高,符合岩石力学性质变化规律。σh的升高幅度与岩石β值有关,当β值较大时(如β=12×10-6/ ℃),地层σh的降低幅度较缓;随着β值的逐步增加,地层σh的升高幅度具有提升的趋势。当ν值较小时(如ν=0.15),岩石具有较小的弹性模量及σh值。整体来看,β值越大,所预测的地层σh值越大,称为热膨胀应力效应[16]。研究区目的层致密砂岩的ν值主要分布在0.2～0.3范围内,热膨胀应力效应对σh的影响十分显著。

将表1中砂岩热膨胀系数区间值代入式(4),对式(4)的可靠性进行判定。研究发现,当β取值为表1中的砂岩最小值5×10-6/ ℃时,σh的预测结果最好;当β取值大于5×10-6/ ℃时,σh的预测效果逐渐变差;同样,当β取值小于5×10-6/ ℃时,σh的预测效果也逐渐变差(见图4)。因此,对于所研究煤系致密砂岩储层,当式(4)中取β=5×10-6/ ℃时,该计算模型最为可靠。因此,也可以判定出该致密砂岩储层的β值为5×10-6/ ℃。

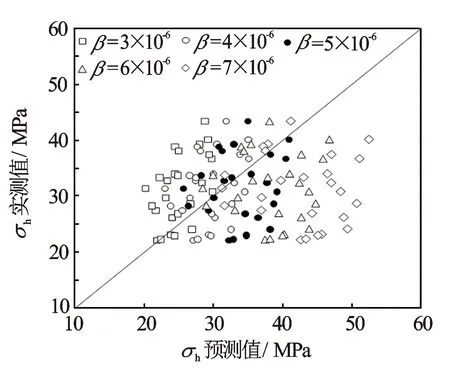
图4 σh预测结果与实测值间对比图

式(4)综合考虑了各弹性参数及温度参数对地层σh的影响。同时,β值取5×10-6/ ℃。在此评价基础上,采用逆向转换分析方法,将σh设定为自变量,ν设定为因变量,即利用σh表征ν,可得

(5)

式(5)即为本文所建立的利用地应力对泊松比进行校正的一般表达式。该表达式适用于鄂尔多斯盆地东北缘埋深较大(2 000 m附近)的煤系致密砂岩储层,对于类似地区致密储层也具有一定参考价值。

4 测井实例分析

对于研究区上古生界煤系地层,β取5×10-6/ ℃,G取0.026 ℃/m。将地应力测井解释成果中的地层σh、σv及H带入式(5),可求取相应深度域的岩石ν值。利用图2所示拟合方程可获得相应岩石E值。应用这种方法分别获取的岩石E值和ν值即为本文逆向运算方法所获取的岩石弹性参数结果。对于常规动静态弹性参数转换方法,采用图1中的拟合关系进行解释。

图5 LX-2S井弹性参数及地应力测井评价成果图*非法定计量单位,1 ft=12 in=0.304 8 m,下同

图5所示为研究区LX-2S井目的层弹性参数及地应力测井评价结果,所解释上古生界地层埋深主要分布在1 200～1 900 m范围,岩性以频繁互层的致密砂岩和泥页岩为主,局部夹煤层或煤线,地应力状态满足σh<σH<σv,与前述压裂法地应力计算结果一致。从评价结果来看,逆向地应力转换方法所确定的ν值要比常规方法(动静态参数转换方法)确定的ν值略小,但2种方法所确定的ν值的变化趋势基本一致。这说明2种结果仅仅存在一个系统误差,这类误差可以通过后续校正而消除。因此,采用常规动静态参数转换方法所确定的泊松比是可靠的,可以用于压裂段的现今地应力测井评价。

对于弹性模量,情况较为复杂。从图5中可以发现2种截然不同的情况:①本文方法所确定的E值与常规方法所确定的E值的变化趋势基本一致。这种情况通常出现在薄砂泥互层段的界面处,并主要表现为低值,如1 215 m处、1 230 m处、1 350～1 360 m处、1 450～1 470 m处等。岩性界面处通常为弱面,岩石易于发生破裂并发生应力卸载[16],地应力值较低;②本文方法所确定的E值与常规方法所确定E值的变化趋势截然相反。该类情况在全井段都是极为普遍的,即本文方法所确定的高E值段,在常规方法解释结果上却表现为低E值(见图5)。这类层段在大段砂岩段及砂泥互层段中出现的频率均十分高,高含气量砂岩段是该地区的主要压裂层段。此时,如果采用常规动静态转换关系所确定的E值进行地应力测井评价,就会造成地应力解释结果误差的扩大。要克服该不足,可以采取2种措施:(1)由于利用动静态参数转换模型进行测井评价的岩石泊松比是可靠的,因此,可选用包含岩石泊松比参数而不含弹性模量参数的地应力测井解释模型,如Terzaghi模型、Anderson模型、安德森模型、Newberry模型及黄氏模型等[2-4];(2)采用本文基于逆向地应力运算检验弹性参数的方法,对地层弹性模量进行测井解释。该方法的具体解释步骤为:①利用实测现今地应力测试结果确定储层地应力大小;②在考虑岩石热膨胀系数(β)基础上,建立利用地应力对泊松比进行校正的一般表达式(本文所建立的公式为式(5));③利用岩石静态弹性模量与静态泊松比之间的定量关系(本文为图2中的拟合关系)完成对岩石弹性模量的测井评价。本文方法克服了压裂层段弹性参数取值可靠度不明的问题,并提出了提高压裂层段弹性参数取值精度的方法。该研究对于指导非常规致密储层现今地应力场精细测井预测具有一定指导意义。

5 结 论

(1) 本文基于逆向转换分析思路,利用压裂法确定煤系致密砂岩储层地应力大小,在考虑岩石热膨胀系数(β)基础上,建立了利用地应力对地层岩石泊松比和弹性模量进行测井评价的方法。

(2) 所研究煤系致密砂岩的E和ν具有非常好的正相关性,该致密砂岩储层的β值为5×10-6/ ℃。采用常规动静态参数转换方法获取的岩石泊松比测井解释结果是可靠的,可以用于压裂段的现今地应力测井评价。对于弹性模量,常规方法在全井段的可靠度均较低,仅在薄砂泥互层段界面处较为可靠。

(3) 为了提高煤系地层现今地应力测井预测精度,建议选用包含岩石泊松比而不含弹性模量的地应力测井解释模型,如Terzaghi模型、Anderson模型、安德森模型、Newberry模型及黄氏模型等;或者采用本文基于逆向地应力运算检验方法对岩石弹性模量进行测井评价。