川南地区乐平组煤层含气量定量评价方法

冯俊贵,芮昀,万金彬,崔式涛,廖茂杰,冯程,赵毅,陈美军

(1.中国石油集团测井有限公司,陕西 西安 710077;2.浙江油田勘探开发研究院,浙江 杭州 311122;3.中国石油大学(北京)克拉玛依校区石油学院,新疆 克拉玛依 834000)

0 引 言

煤层气作为非常规能源,其煤储层含气量的定量预测是评价的关键。目前国内外煤层含气量预测方法主要有直接法、解吸法和间接法[1]。直接法是对煤岩密闭取心在实验室测试,模拟地层温度和压力条件下测定单位重量煤含气体积;解吸法是利用解吸仪测定解吸量随时间的变化规律,基于测定井筒煤层气解吸速度的直接测定煤层含气量的方法;间接法主要分3类:第1类是基于煤层气等温吸附模型的含气量计算,包括基于经验式的Freundlich模型、基于单分子吸附层的Langmuir模型(兰氏模型)、基于多分子吸附层的BET方程以及微孔填充吸附理论的(D-R方程)、BET方程改进型、D-A方程、Kelvin方程(通常会出现IV和V型等温线)等。目前对于煤层中水分含量介于0和饱和水分之间的吸附等温线主要用Langmuir模型[2]。第2类是非线性信息预测法,包括最优化、遗传算法、BP神经网络、支持向量机、小波变换以及灰色系统理论等非线性处理方法[3]。第3类是统计回归预测法[4],优选影响煤层含气量的敏感性测井参数,构建敏感参数与含气量的解释模型,经直接法和吸附法刻度,定量预测含气量。目前统计回归方法包括单参数回归和多元回归。其中单参数回归方法有Mullen和Mavor[5]最早提出用密度测井资料计算煤层含气量的Mullen公式和Mavor公式,其次是地区经验密度值计算法、中子计算法、电阻率法、消除中子或密度背景值法。单参数回归方法考虑因素单一,所以计算快,但计算误差大(输入曲线易受外界干扰),相关性差;而多参数回归方法是基于煤层含气量有关的多个测井敏感参数,经曲线重构和敏感参数优选,建立含气量多元回归模型。多元回归模型由于考虑影响含气量的多方面因素,有效减小单一参数风险,且通过对相关性小的多个测井参数采取曲线重构降元处理,进一步减小预测误差的可能性。将预测结果与直接法测量结果拟合,相关性基本在80%以上。

1 影响煤层含气量的测井敏感参数分析

选取浙江油田筠连沐爱核心区煤心实验分析的井,在岩心归位的基础上,建立煤心测试空气干燥基含气量分别与自然伽马、补偿密度、补偿中子、声波时差、深电阻率对数以及煤层埋深的交会关系,按照相关系数大小量化排列各条测井曲线敏感性。煤层含气量敏感性最好的是自然伽马GR和补偿密度DEN,其次是补偿中子CNL、补偿声波时差AC和深电阻率对数,最差是埋深H(见图1)。该研究区埋深与含气量呈多项式相关,煤层埋深在750 m左右含气量达到最大,大于750 m含气量逐渐递减,这与研究区地层温度和压力有关。

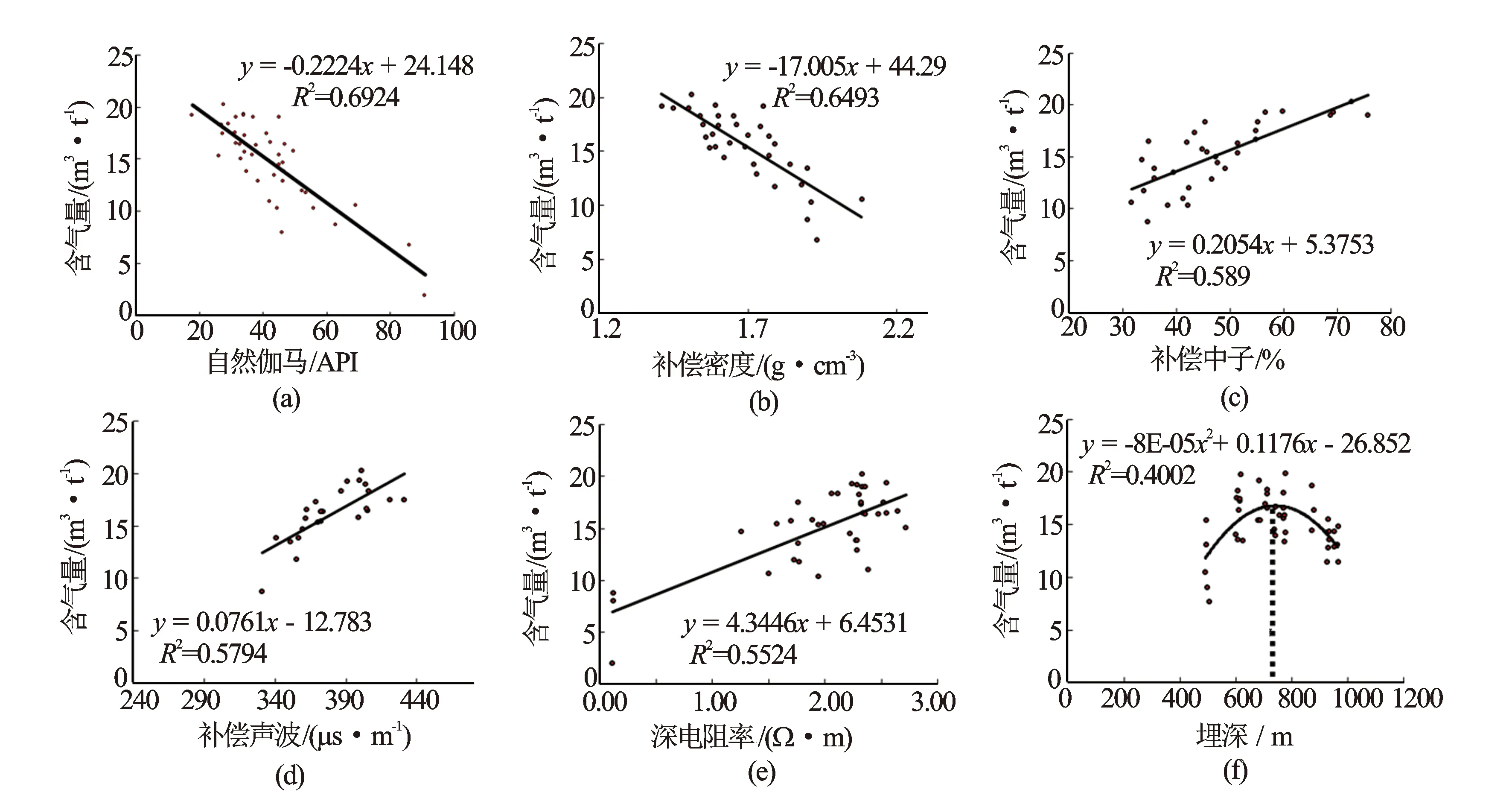
图1 测试含气量与测井敏感参数的交会关系

2 基于测井敏感参数的煤层含气量计算

2.1 吸附模型计算含气量

研究区煤阶为中高阶煤,温度适中,吸附方式多为单分子层吸附,符合基于单分子吸附层的Ⅰ型的Langmuir模型(兰氏模型)。利用测井敏感参数构建兰氏体积和兰氏压力,其中兰氏体积与煤阶相关性强,而煤阶可通过测井敏感参数求取;兰氏压力取决于固定碳和地层温度。Langmuir模型为

(1)

式中,V为含气量,m3/t;VL为兰氏体积,表示吸附达到饱和时所吸附的气量,是衡量煤岩吸附能力的量度,其值反映了煤的最大吸附能力,m3/t;p为地层压力,MPa;pL为兰氏压力,表示吸附量达到饱和吸附量一半时的压力,MPa。

含气量V为煤层最大吸附气量,不代表煤层实际含气量,需要作进一步校正。在实际计算中,考虑到煤岩中含有灰分等非碳组分,通常将煤质组分和含气量联系建立兰氏方程,并且需考虑实际状态下的温度和海拔深度的影响,公式为

(2)

式中,Vaad为灰分含量,%;Vmad为水分含量,%。

由物质平衡理论,式(2)中(1-Vaad-Vmad)=VFC+VVM(式中,VFC为固定碳含量,%;VVM为灰分,%),对煤层工业组分分析得出VVM较小,因此近似为计算固定碳含量VFC。由图2,固定碳含量VFC与灰分Vaad相关系数达到0.958,而灰分VVM与补偿密度DEN相关系数达到0.874。因此,可以用补偿密度做敏感参数求取固定碳含量VFC

(1-Vaad-Vmad)≈VFC=-78.3DEN+189.62

(3)

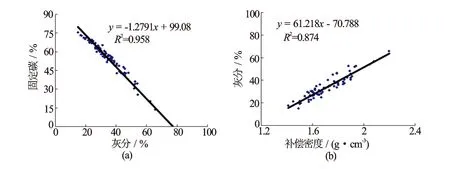
图2 灰分、补偿密度与固定碳关系

经对研究区煤心实验室等温吸附实验分析,反应煤阶的最大镜质体反射率Ro与兰氏体积VL存在非线性多项式关系(见图3)。Ro是划分煤阶的重要指标,在同一温度和压力下,兰氏体积随煤阶的增加单调递增。

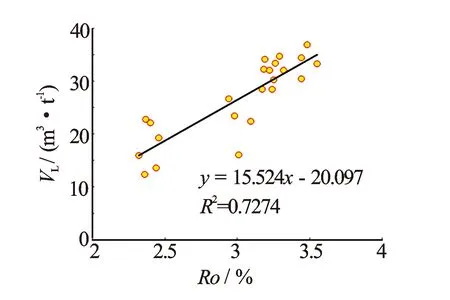
图3 兰氏体积VL与最大镜质体反射率Ro关系图

将通过最大镜质体反射率Ro拟合得到的VL代入式(2),得到

(4)

VL=f(Ro)=-91.704Ro2+681.3Ro-1222.1

(5)

经测井敏感性参数分析,Ro与煤层埋深、自然伽马、补偿密度、补偿声波、补偿中子、深电阻率相关,其中Ro与煤层埋深、深电阻率、声波时差、自然伽马、补偿密度正相关,与补偿中子呈负相关

Ro=f(H,AC,CNL,DEN,GR,Rd)=a×H+b×GR+c×DEN+d×AC+e×Rd-f×CNL

(6)

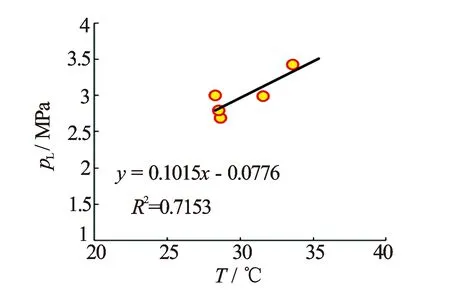
图4 储层温度与兰氏压力pL关系图

式中,a、b、c、d、e、f为回归系数;H为深度,m;GR为自然伽马,API;DEN为补偿密度,g/cm3;AC为补偿声波,μs/m;Rd为深电阻率,Ω·m;CNL为补偿中子,%。

U.Ahmed将兰氏方程改进为

pL=f(VFC,T)

(7)

式中,T为地层温度,℃。

通过对本研究区等温吸附实验分析,兰氏压力与温度相关性较高,相关系数为0.7以上(见图4),两者相关性为

pL=0.1015T-0.0776

(8)

从理论分析,煤层埋深、补偿密度和补偿声波时差均能反应地层压力p。对研究区经测井敏感参数分析,煤层埋深的相关性达0.8以上,故优选煤层埋深H为计算地层压力参数,得出

p=78.323H+201.35

(9)

该含气量计算模型是基于兰氏方程,经测井敏感参数构建煤阶Ro,由煤阶和兰氏体积关系进而求取兰氏体积,再优选影响兰氏压力和地层压力的测井敏感参数,定量求取煤层含气量。该计算模型考虑煤层埋深、温度、煤阶、煤组分工业含量等多种因数,从而减小煤层含气量计算误差。

2.2 多元回归模型计算含气量

经对研究区煤心测试含气量与测井曲线相关性分析,提取出计算含气量的测井敏感参数,得出相关性由大到小:自然伽马、补偿密度、补偿中子、补偿声波、深电阻率以及埋深。剔除相关性最差的埋深参数,运用多元回归法对前5个测井参数构建含气量计算模型。分别对5个测井参数进行多元回归求取含气量,求得相关系数R2=0.868 9;对敏感性较差的补偿中子、深电阻率的参数经降元处理,构建复合参数L(CNL,lnRt),求得相关系数R2=0.889 7,与第1种方法相比,计算精度进一步提高(见表1)。

表1 煤层含气量多元回归计算模型

2.3 模型适用性分析

2.3.1 模型有效性

为验证2种预测模型的有效性,分别将2种模型计算含气量与实验室测得的空气干燥基总含气量进行相关分析,得出基于吸附模型计算的含气量相关系数为0.864 6,基于多元回归模型计算的含气量与实验室测得含气量相关系数为0.778 2。基于吸附模型计算的含气量精度更高(见图5)。

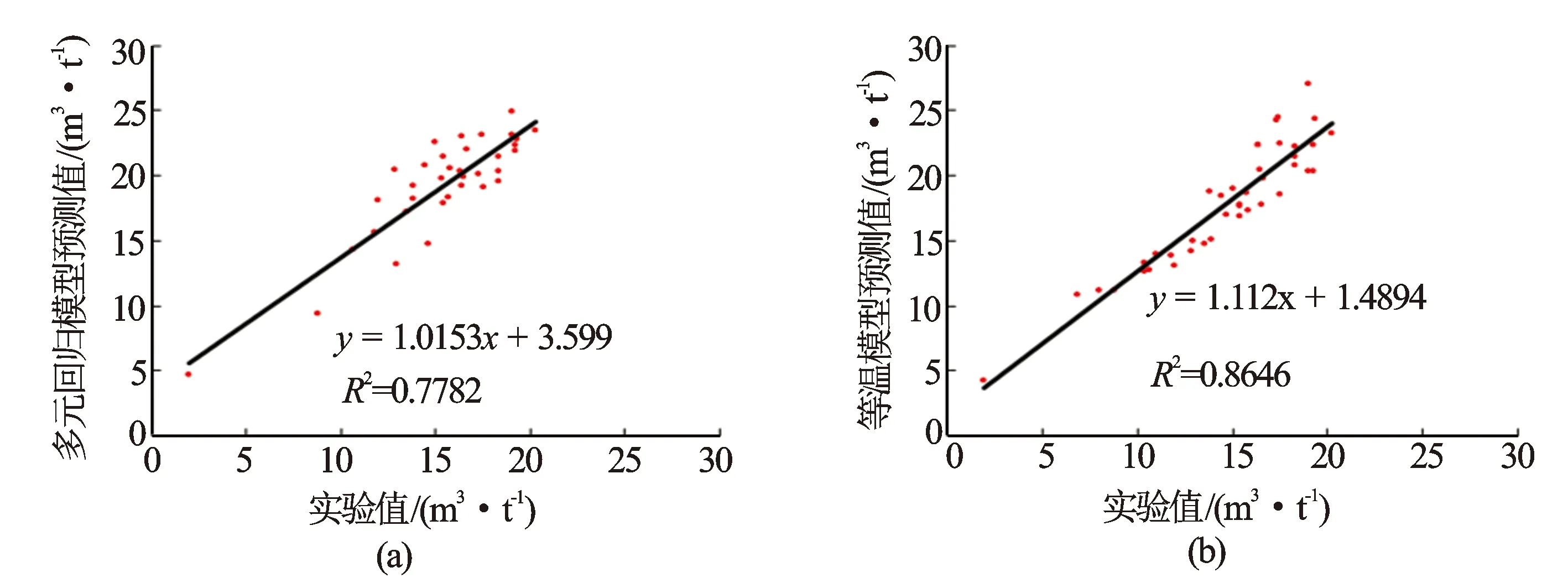
图5 多元回归模型、吸附模型含气量预测值与实验值对比图

2.3.2 数据误差分析

进一步检查样本数据可靠性,分别运用吸附模型和多元回归模型对研究区YSL12井8号煤层样本数据进行预测。预测结果表明,吸附模型计算的绝对误差较多元回归法小,平均绝对误差为1 m3/t;吸附模型计算的相对误差在10%以内,多元回归法的相对误差平均值在20%。

通过模型有效性和计算误差比较认为,吸附模型计算精度更高,计算结果更可靠,在该研究区具有更好的应用价值。

2.4 应用实例

在川南地区筠连区块运用等温吸附模型和多元回归模型分别对煤层8进行含气量预测。图6第6道为YS12井煤层8分别进行实验室煤心空气干燥基测试含气量、多元回归模型以及吸附模型预测含气量比照。从第6道看出,2种模型均能较好预测含气量。第7道和第8道分别为多元回归模型和吸附模型计算含气量分别与煤心含气量刻度,吸附模型预测值整体明显高于多元回归模型,且吸附模型预测值更接近实验室测试值。

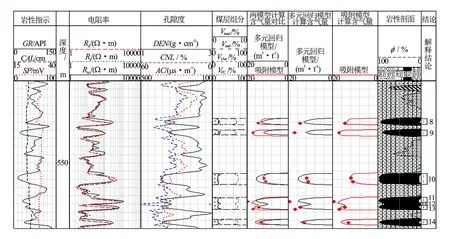
图6 川南地区筠连区块YS12井8号煤层含气量计算模型效果

综上所述,吸附模型在该研究区定量预测煤层含气量方面具有更高的精度,可在该研究区推广应用。

3 结 论

(1) 煤层含气量计算方法主要有直接法、解吸法和间接法,间接法成本低,分辨率高,能弥补直接法和解吸法煤心分析、取样的不足。具体方法的选取要依据不同地区、不同煤质,针对性地选取最优预测模型。

(2) 影响煤层含气量的测井敏感参数分析表明,自然伽马、补偿密度与含气量相关性很好,补偿中子、补偿声波时差和深电阻率对数相关性较差,建议在多参数预测模型中将相关系数差的参数构建复合参数,提高预测精度。

(3) 基于测井敏感参数构建的多元回归模型含气量预测值与实验室测量值相关系数为0.778 2,相对误差在20%左右;吸附模型预测值与测量值相关系数为0.864 6,相对误差在10%左右。 说明2种方法在该研究区均适用,但吸附模型预测含气量更准确。