与XY双自旋链耦合的双量子比特系统的关联性与相干性∗
杨阳 王安民 曹连振 赵加强 逯怀新
1)(潍坊学院物理与光电工程学院,山东省多光子纠缠与操纵实验室,潍坊 261061)2)(中国科学技术大学近代物理系,合肥 230026)(2018年4月25日收到;2018年5月20日收到修改稿)
1 引 言
量子相干性源于量子力学的叠加原理,在量子信息处理中扮演着重要的角色.比如在纠缠产生[1,2]、量子计量学[3−5]、量子热力学[6−8]以及量子生物学[9−11]中都有着广泛的应用.
Baumgratz等[12]提出了一个量化量子相干性应满足的条件.多个量子相干度量方法随之被提出,比如相对熵相干度量和l1范数相干度量,二者都是基于所考察量子态与非相干态集合间的某种最小距离而定义的.基于凸顶方法的生成度量[13,14]、基于操作[15,16]以及基于量子纠缠[2]的相干度量也相继被提出.在准确度量相干态相干性的基础上,人们对量子相干性的多个方面展开研究,比如量子相干性与量子纠缠的转化[17,18].量子关联在量子算法[19,20]、远程量子态制备[21]等量子信息任务处理中同样扮演着重要的作用,因此量子相干性与量子关联的关系也引起了人们的关注[22−24].
现实中,量子系统不可避免地要与环境发生相互作用而丢失相干性,进而不能有效地执行量子信息处理任务.量子关联在实际处理任务中,也遭到环境噪声的破坏,但是无论是Markovian还是非Markovian环境,人们对量子关联的破坏研究相对较多[25−28].量子关联可以不受某些具体噪声的影响而保持不变,同时量子关联与经典关联之间存在突变效应[29−34].Bromley等[35]首先发现对于某些特定的量子系统,当体系处于某些特殊的初态时,基于距离的量子相干度量保持不变,即会发生相干冻结现象.Yu等[36]给出了量子系统的相干性完全冻结的条件.相干性一旦遭到破坏,量子系统处理量子信息任务的能力也随即被破坏.所以环境作用下量子系统相干性演化规律吸引了众多学者进行研究[37−44].本文主要研究自旋链环境作用下,系统相干性与关联性的演化规律.
本文将具有Dzyaloshinsky-Moriya(DM)相互作用的XY自旋链作为量子系统所处的环境,考虑双量子比特系统的量子态的演化规律,推导出某些初态的相干性演化公式,并与系统的关联相比较.我们发现量子相干性在不同的时间段有不同的对应,在t
2 双XY自旋链中双量子比特的演化
由两个无相互作用的自旋组成的双量子比特A,B构成的系统在具有DM相互作用的独立XY自旋链环境下的哈密顿量为



σi(i=x,y,z)为泡利算符.系统的密度算符演化为其中,λg= λ.利用Jordan-Wigner与Bogoliubov变换,可以被对角化为[45−47]

其中

εµ= λµ− cos(2πk/N),k= −M,···,M, 且M=(N −1)/2.HλµE对应的基态
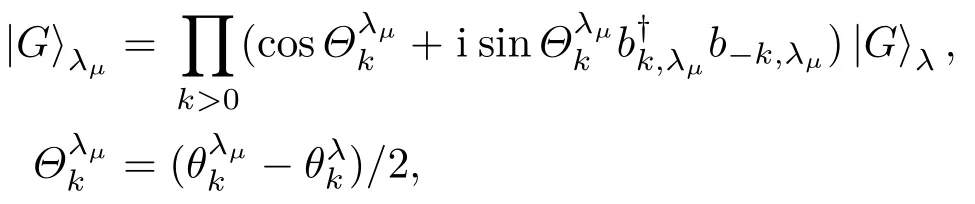

与XY自旋链相比较,具有DM相互作用的XY自旋链有明显的区别,一是能谱中含有相互作用强度D,二是中含有Bogoliubov变换角度因此DM相互作用可能对量子相干性产生影响,其影响将由|F(t)|的具体表达式

来决定.
3 量子失协与量子相干度量
量子失协被用来量化量子关联,是由经典互信息过渡到量子情形下所产生的差异而来[48].对双量子系统,其定义为

其中I(ρ),Cc(ρ)分别为总关联、经典关联;

Baumgratz等[12]给出了严格量化量子相干性所应满足的条件:(i)非负性,C(ρ)>0,只有非相干态才等于零;(ii)单调性,C(ρ)>C(Λ(ρ)),Λ为非相干操作;(iii)强单调性,其中λ为非相干操作,(iv)凸性,C(qρ+(1−q)τ)6 qC(ρ)+(1−q)C(τ).基于此,相对熵相干度量被提出,其定义为
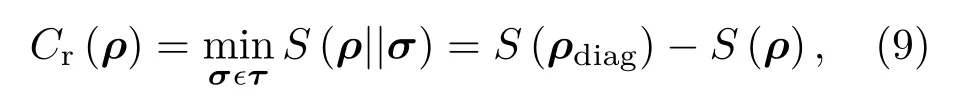
其中τ为非相干态集合,ρdiag为ρ的对角元组成的矩阵.
4 量子相干动力学
不失一般性,选取c1=1,c2=−c3,由(8)式得双量子比特系统的总关联为

其中
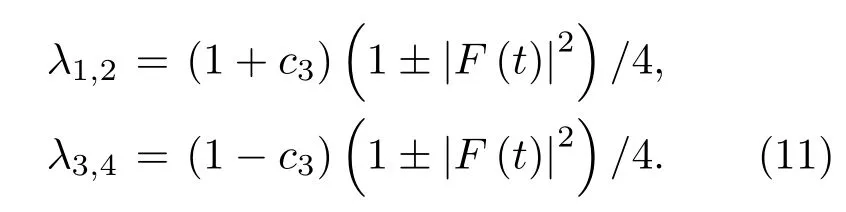
系统的量子关联为
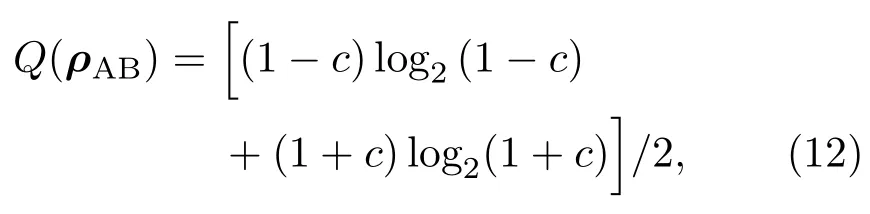
由(9)式得系统的相对熵相干度量为

利用量子关联或者相干性都可以探测到XY自旋链在λ=1处存在相变点[33].现在主要考虑相变点λ=λc=1附近的关联以及相干性的演化情况.选取δ=0.1,γ=0.5,c3=0.8,N=401时,图1(a)展示了D=0时关联与相对熵相干度量的演化.发现在t=t0处量子关联与经典关联存在突变,突变时刻t0满足|F(t0)|2=c3.当t
图2展现了不同各向异性参数γ对量子相干性与关联的影响,其中δ=0.1,D=0,c3=0.8,N=401.随着各向异性参数γ的增加,退相干效应加快,这与中心双量子比特系统与一条XY自旋链的耦合情形相似[45,46].而当选取γ=0.5,D=0,c3=0.8,N=401时,图3展示了不同耦合强度δ下的量子关联与退相干的演化.我们发现耦合强度δ同样能使相干性与量子关联的衰变加快.
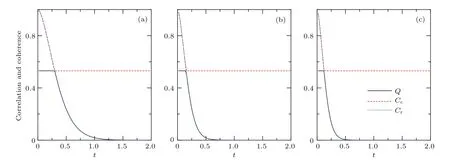
图1 不同DM相互作用下关联性与相干性的演化规律 (a)D=0;(b)D=0.4;(c)D=0.6Fig.1.The evolution of correlations and coherence for dif f erent values of the DM interaction:(a)D=0;(b)D=0.4;(c)D=0.6.

图2 不同各向异性参数下关联性与相干性的演化规律 (a)γ=0.2;(b)γ=0.4;(c)γ=0.6Fig.2.The evolution of correlations and coherence for dif f erent values of the anisotropy parameter:(a)γ=0.2;(b)γ=0.4;(c)γ=0.6.

图3 不同耦合常数下关联性与相干性的演化规律 (a)δ=0.2;(b)δ=0.4;(c)δ=0.6Fig.3.The evolution of correlations and coherence for the dif f erent coupling constants:(a)δ=0.2;(b)δ=0.4;(c)δ=0.6.

图4 γ=0.5,D=0,c3=0.8时不同自旋链粒子数与耦合常数下量子关联与量子相干的演化规律Fig.4.The evolution of quantum correlation and quantum coherence for dif f erent values of size of the chain and coupling constants at γ=0.5,D=0,c3=0.8.
5 结 论
本文研究了双量子比特系统分别独自与具有DM相互作用的XY自旋耦合下的量子相干性与关联动力学.量子相干性与量子关联分别采用相对熵、量子失协来度量.推导出了相干性与关联性的演化规律.发现在自旋链的临界点附近,系统相干性的演化与关联的演化存在统一性.在量子关联未衰变阶段,相干性的演化与经典关联的演化完全相同,而后则与量子关联的演化完全相同.此外,还发现各向异性参数γ、DM相互作用强度D以及耦合强度δ并不改变量子相干性以及关联的演化特点,但随着参数增加会使相干性及关联性的衰变加快.

