期刊影响力指数排名的合理性分析

■洪寒梅 陈 妍 钱欣平 祁建琴

浙江大学出版社期刊中心，浙江省杭州市天目山路148号 310007

期刊影响力的评价、排名能给决策部门提供依据，可为期刊的发展提供参考，也影响作者投稿时的期刊选择。研究者侧重于对期刊进行排序，以此反映期刊的影响程度[1]。学者们致力于提出一种可以充分反映期刊情况的评价指标体系。常用的期刊评价指标有影响因子(Impact Factor，IF)、5年影响因子(5-Year Impact Factor，IF5)、即年指标(Immediacy Index，IM)、总被引频次(Total Cites，TC)等，但是各有其局限性[2]。例如，IF最早由Garfield[3]提出，把时间跨度定为2年，而事实上，不同学科、不同类型的学术期刊被引高峰期存在明显差异，有的超过2年，现行的影响因子不能反映某些期刊的真实学术水平[1]。正如Bollen等[4]所言，任何一个指标都不能独立承担期刊评价工作。

中国科学文献计量评价研究中心在《中国学术期刊国际引证报告(2013年)》提出了一个新的综合评价指标——期刊影响力指数(Clout Index, CI)。自提出以来， CI连续4年应用于“中国最具国际影响力学术期刊”的遴选，得到了国内外学术界和期刊界的基本认可[5]。2014年之前，《中国学术期刊影响因子年报(自然科学与工程技术)》(以下简称“《年报》”)以复合IF作为期刊影响力排名依据。自2015年起，《年报(2015)》[6](统计2014年的数据)将各期刊的CI值(fCI)作为期刊影响力排名依据。CI在IF的基础上考虑了TC指标，兼顾了期刊发展历史、发文量等规模因素对期刊影响力的作用，优于IF指标。对2017年《期刊引证报告》(JournalCitationReports，JCR)中公布的期刊信息按照fCI重新划分Q1～Q4区，发现Q1区的变化率为19%。对SCI收录期刊的排序结果也表明，相比IF，CI排名结果更接近人们的认知[2]。

CI是反映期刊影响力大小的综合指标，是将期刊统计年的TC和IF双指标进行组内线性归一后向量平权计算所得的数值，用于对组内期刊排序。fCI的计算公式为

(1)

(2)

(3)

式中fIF为期刊的他刊影响因子，fIFmin为组内fIF的最小值，fIFmax为组内fIF的最大值，fTC为他刊总被引频次，fTCmin为组内fTC的最小值，fTCmax为组内fTC的最大值。统计源包括期刊类统计源、博士学位论文统计源和会议论文统计源[5]。《年报(2016)》对量效指数(Journal Mass Index,JMI)低于阈值的期刊fCI进行了修正：

(4)

式中k为他引频次调整系数[5]。

曾有研究表明，仅根据期刊的TC和IF 2个评价指标作散点图进行对比，不能全面地反映评价指标间的特征，也不能揭示期刊之间的综合质量和水平[7]。那么，考虑TC和IF 2个指标的fCI是否能够科学、全面地评价期刊影响力？

俞立平等[8]指出，TC与其他影响力指标的相关性弱，不能很好地反映年度期刊影响力，可能仅反映了期刊的办刊历史。由(1)～(4)式可知，fCI把TC和IF作为相互独立的指标，而事实上，TC和IF存在一定的相关性，例如2016年版JCR期刊的IF和TC的相关性系数R≈0.40[2]。由(4)式可知，TC和IF是所有指标中最能代表期刊影响力的指标。事实上，2016年版JCR期刊的IF与IF5的相关系数R≈0.98，IF与IM的相关系数R≈0.83[2]，IF能在较大程度上代表IF5，但不能完全代表。因此，从表征程度角度分析，fCI的计算公式存在不完全性。

在《年报(2015—2017)》的期刊影响力指数及影响因子表中，除了CI以外，还呈现了以下10项指标：复合总被引、复合类IF、复合类他引IF、复合类IF5、复合类IM、期刊综合总被引、期刊综合类IF、期刊综合类他引IF、期刊综合类IF5、期刊综合类IM。

期刊评价指标之间往往存在多重共线性，常用的消除方法是因子分析或者主成分分析降维处理法[9]。张弘等[10]指出，使用主成分分析法评价科技期刊可以消除指标间的相关性带来的评价偏差，降低指标维数和指标的选择难度；可以消除人为确定指标权重引起的弊病，使评价结果更具客观性和准确性；可以有效消除自引过高导致IF失真对期刊评价带来的负面影响。辛督强[11]采用主成分分析方法对13种力学类中文期刊进行综合评价，认为基于主成分分析的期刊综合排名是期刊文献质和量相统一的结果，与绝对量指标的关联度高于与相对量指标的关联度。管进[12]认为主成分分析法不仅可以在众多指标中指出决定核心期刊的主成分，而且可以通过统计方法科学地确定各成分的权重，是一种科学、可行的方法。俞立平等[13]采用聚类分析和因子分析方法进行期刊评价指标分类，发现因子分析法的解释力强，是一种较好的学术期刊评价指标分类方法。余以胜等[7]采用主成分分析法对25种计算机科学技术类期刊进行排序，并评价期刊的质量和水平。一方面，以上研究表明主成分分析方法适合用于分析期刊评价指标；另一方面，以上研究均没有涉及CI(有些研究的发表时间早于CI的提出时间)。目前，CI作为期刊排名依据已经有3年，尚未有学者对其科学性作出分析评价。

本研究以2017年第15卷、2016年第14卷和2015年第13卷“N/Q、T/X综合性科学技术”中423、424、422种期刊的数据为研究对象，采用主成分分析评价方法，通过相关系数矩阵的特征向量将评价指标线性变化成彼此独立的主成分，通过特征值确定主成分的取用维数和权重，将主成分加权求和得到评价值。根据综合主成分值F对样本期刊进行排序，将排序结果与fCI的排序结果进行对比；计算并比较F和fCI与10项指标的相关性；分析fCI排名的科学合理性，探讨其存在的不足。

1 数据获取

本研究的原始数据来自中国知网评价中心[14]。得到的数据为PDF格式，为了方便统计分析，采用ABBYY FineReader 14将PDF文件转换为Excel文件[15]，并删去Excel中有空值的行，即删去指标信息不全的期刊，最后获得2017年第15卷371种期刊的数据、2016年第14卷384种期刊的数据和2015年第13卷371种期刊的数据。

2 主成分分析排名

采用主成分分析法对2017年的样本数据进行处理[16]，所建立的评价指标体系如表1所示。X1～X5为复合类指标，统计源包括期刊统计源、博硕士学位论文统计源、会议论文统计源。X6～X10为综合类指标，统计源为期刊类统计源[6]。采用IBM SPSS Statistics 24软件对样本数据进行分析，具体实验操作过程如下。

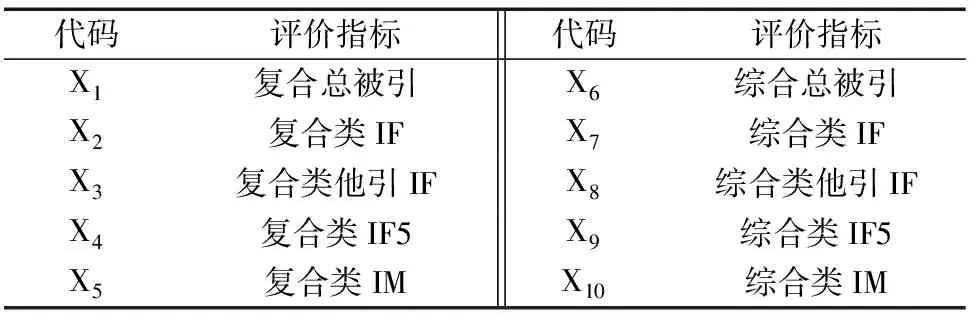
表1 评价指标体系

2.1 KMO和Bartlett球度检验

KMO(Kaiser-Meyer-Olkin)检验统计值是用于比较变量间简单相关系数和偏相关系数的指标[16]。KMO值越接近于1，变量间的相关性越强，原有变量越适合作因子分析。采用IBM SPSS 24.0软件中“分析—描述统计—描述”得到数据的标准化值，采用“分析—降维—因子”将数据进行KMO和Bartlett球形度检验，结果如表2所示。

表2 KMO和Bartlett球度检验结果

KMO检验统计量分别为0.689、0.712、0.717，根据Kaiser给出KMO度量标准可知，原有变量适合进行主成分分析[17-18]。 Bartlett球度检验的近似卡方值分别为11141.384、11580.435、11223.114，p均小于0.001，Bartlett球度检验接受零假设。因此，样本数据适合作主成分分析[18]。

2.2 主成分分析

以2017年的样本数据为例，进行主成分分析。表3为因子分析中的共同度表，提取值≥0.820，X2、X3、X4、X7、X8、X9对应的提取值在0.9左右，所有变量的共同度都较高，各个变量丢失的信息较少，说明绝大部分信息可以被因子解释，所建立的主成分分析模型对原变量的解释力较强，同时说明了所选指标的合理性。

表3 因子分析中的共同度

图1为主成分分析得到的碎石图，横坐标为主成分编号，纵坐标为特征值。由图1可知：第1个因子的特征值(方差贡献率)很高，对解释原有变量的贡献最大；第3个及以后的因子特征值都较小，对解释原有变量的贡献很小，已经成为可以忽略的“碎石”，因此提取前2个主成分。

图1 主成分分析的碎石图

主成分特征值及方差贡献率见表4，其中，第一主成分的贡献率为74.706%，前2个主成分的累积贡献率为87.211%，反映了绝大部分信息可以接受。特征值为λ1=7.471，λ2=1.250。

表4 主成分特征值及方差贡献率

对应的主成分初始因子载荷矩阵如表5所示，其中B1和B2分别表示第一、二主成分与对应变量的相关系数，ZXi为原始变量标准化后的值。由表5可知，第一主成分中复合类IF、复合类他引IF、复合类IF5、综合类IF、综合类他引IF、综合类IF5的载荷分别达到0.948、0.937、0.949、0.943、0.952、0.960。因此，第一主成分主要代表期刊的影响因子。相应地，第二主成分中复合总被引、复合类IM、综合总被引、综合类IM的载荷分别达到0.583、-0.527、0.542、-0.577。因此，第二主成分代表了期刊的总被引频次和IM。因此，提取前2个主成分基本可以反映全部指标的信息。

表5 主成分分析的初始因子载荷矩阵

用表5中的载荷矩阵除以主成分相对应的特征值开平方根便得到前2个主成分中每个指标所对应的系数[16]，即

(5)

由此得到的特征向量如表6所示。

表6 主成分特征向量

分别将特征向量A1、A2与标准化后的数据相乘，得到第一主成分F1和第二主成分F2，计算得到综合主成分值[16]：

(6)

由此计算得到的F如表7所示。

表7 采用主成分分析得到期刊的fCI和F

3 结果与讨论

3.1 主成分分析与fCI的排序结果对比

根据以上步骤计算得到各期刊的F值，并对期刊进行排序。2015—2017年按F值排名前15的期刊如表8～10所示。

由表8～10可知：2015年排序差异较大的是《兰州大学学报(自然科学版)》《实验技术与管理》、JournalofZhejiangUniversity-ScienceA(AppliedPhysics&Engineering)、《西安科技大学学报》《江苏大学学报(自然科学版)》；2016年排序差异较大的是《南京信息工程大学学报(自然科学版)》《南京大学学报(自然科学版)》《自然杂志》《西安科技大学学报》；2017年排序差异较大的是《中国科学院院刊》《实验技术与管理》《西南交通大学学报》《吉林大学学报(工学版)》《清华大学学报(自然科学版)》、ScienceChina(TechnologicalScience)。其中，《中国科学院院刊》在2015年和2016年的F排名第1，而fCI排名都是第6；该刊2017年的F排名第2，而fCI排名是第15，相差较大。此外，《科学通报》无论是哪种排序方法都十分靠前，2015年和2016年F排名第2，fCI排名第1，2017年F和fCI排名都是第1，体现了该刊的实力。2015—2017年fCI排名都位列第2的ScienceBulletin，在F排名中却不够稳定，2015年位列第7，2016年和2017年均位列第3。

表8 2015年F值排名前15的期刊

表9 2016年F值排名前15的期刊

表10 2017年F排名前15的期刊

3.2 存在差异的原因分析

为了比较fCI和F在期刊影响力排序方面的科学性和实用性，采用IBM SPSS 24软件分别计算fCI和F与10个指标的相关性。该软件中提供了3种相关系数计算方法：Pearson、Spearman和Kendall[18]。其中，由于期刊各个指标之间的线性关系较弱，并且大多数不服从正态分布，因此选用Spearman计算方法[19]。Spearman秩相关系数是一个非参数性质(与分布无关)的秩统计参数，用来度量双变量之间的联系强弱程度[20]。本研究采用Spearman计算方法求得的F和fCI与10个影响力评价指标相关系数，结果如表11所示，所有值在0.01级别(双尾)显著性相关。2015—2017年F和fCI与10个原有评价指标的相关性对比如图2所示。

表11 fCI和F与10个影响力评价指标的相关性对比

图2 F和fCI与10个影响力评价指标的相关性对比。(a)2015年；(b)2016年；(c)2017年

由图2可知，整体而言，F和fCI与10个指标的相关程度总体较高，大部分都大于0.9，说明这两者都可以较好地表征这10个指标。2015年的fCI和F与各指标的相关性非常接近，几乎吻合。2016年和2017年的F与10个指标的相关性整体高于fCI。

2015—2017年，F与fCI与指标X5(复合类IM)和X10(综合类IM)的相关性几乎都低于与其他指标的相关性。IM是指某期刊在统计年发表的可被引文献在统计年被统计源引用的总次数与该期刊的当年发表的可被引文献总量之比，表征期刊的即时反应速率[21]和被引强度。因此，相对而言，fCI和F排名不能很好地反映期刊在统计年的被引强度。对比可知，F与指标X5和X10的相关性明显高于fCI，即F比fCI更能表征期刊的及时反应速率。因此，2种综合评价方法存在差异的主要原因是F与fCI对复合(综合)IM的反应能力不同。例如《实验技术与管理》的F和fCI差异较大，原因是该刊近几年发展较好，IM排名上升，使得F排名比fCI更靠前。总之，以上差异的原因是fCI的计算基于TC，TC是一个存量指标，不能进行流量评价[22]。因此，在按照fCI排名的《年报》中，IM由于与fCI的相关性低，具有一定的独立性，比其他指标更具客观性，读者在参阅该《年报》时应当注意期刊的IM。

F更多地考虑了期刊的及时反应速率，因此在由F得到的排名表中，一些fCI排名靠后的期刊因被引强度高而跻身前列，例如2015年JournalofZhejiangUniversity-ScienceA(AppliedPhysics&Engineering)，2016年《南京信息工程大学学报(自然科学版)》，2017年《中国科学院院刊》等，如表12～14所示。JournalofZhejiangUniversity-ScienceA(AppliedPhysics&Engineering)2015年的被引强度非常高，而2016年骤然下降，2017年有明显提升，该刊的fCI排名稳步上升，而F排名随着IM的变化出现较大的波动。《南京信息工程大学学报(自然科学版)》即年指标排名一直较靠前，F排名较好，但是fCI排名非常靠后。《中国科学院院刊》2015—2017年的被引强度逐年攀升，而fCI排名在2017年大幅度下降，F排名基本稳定。

表12 2015—2017年Journal of Zhejiang University-Science A (Applied Physics & Engineering)即年指标及其排名与fCI、F排名

表13 2015—2017年《南京信息工程大学学报(自然科学版)》即年指标及其排名与fCI、F排名

表14 2015—2017年《中国科学院院刊》即年指标及其排名与fCI、F排名

综上可知，fCI排名不能反映期刊当年的突飞猛进，也不能体现期刊当年的一落千丈，是对期刊历年来的发展状况的保守评价。一些资质较深、根基较好的期刊，即使近年来被引强度低，一般也可以获得较好的fCI排名。综上可知，fCI排名对期刊进展的灵敏度低，而F排名可以及时地反映期刊当年的发展情况，从F排名更能看出期刊的进步速度、发展态势和生命活力。对于以促进学术传播为已任、特别注重时效性的学术期刊而言，更多考虑IM的F排名具有不容忽视的参考价值。

4 结论

fCI排名可以较好地表征10个期刊影响力评价指标，但是F与各指标的相关性更高，F排名对10个指标的反应能力高于fCI。

根据F得到的期刊影响力排名与《年报》中按照fCI的排名存在差异，原因是两者不同程度地考虑了期刊的即年指标。fCI排名更好地反映了期刊的根基和发展稳定性，而F排名比fCI排名更及时地反映了期刊在统计年的发展态势，从F排名更能看出期刊的生命活力。fCI排名注重期刊的“过去”和“现在”，而F排名反映期刊的“现在”和“将来”。

在《年报》的“期刊影响力指数及影响因子”表中，IM由于与fCI具有一定的独立性而具有客观性，读者在参阅《年报》时，除了按照fCI的排名结果评估期刊的影响力外，还应当参考对应的IM，以便更加客观合理地评价期刊，考量不同期刊的发展前景。

本研究虽然有充足的横向数据样本，但是由于fCI排名仅实践了3年，纵向数据样本有限，分析结果存在一定的局限性。fCI排名实践多年以后，可以进一步分析fCI的科学性。