青岛地区CORS反演水汽中大气加权平均温度模型的建立

李斐,刘智敏,2,李洋洋,郭金运

(1.山东科技大学,测绘科学与工程学院,山东 青岛266590; 2.海岛(礁)测绘技术国家测绘地理信息局重点实验室,山东 青岛 266590)

0 引 言

水汽在大气中仅占0.11%～3%,但其空间分布极不均匀,时空变化很大,是大气中最活跃的成分。水汽驱动着地球的能量传输和气候演变,对监测和预报短期降水、预防灾害天气起关键作用[1]。因此,时空分辨率高的水汽资料对提高中小尺度的数值天气预报与监测精度至关重要[2]。目前,探测大气水汽主要有无线电探空、微波辐射计、卫星遥感等方式,而无线电探空技术的时空分辨率低,微波辐射计价格昂贵且易受云层厚度和背景温度的影响,卫星遥感时间分辨率低。地基GPS气象学具有全天候探测、连续获取能力强、无需对仪器定标、设备消耗低且相对低廉、探测时空分辨率高等特点,大大提高了水汽资料的精度。在地基GPS气象学中,测量水汽总量的思想就是基于测量天顶方向的湿延迟,通过水汽转换参数获取水汽总量的,而水汽转换参数中的关键参数就是大气加权平均温度,当Tm有5K的不确定度时将导致大气水汽总量产生1.6%-2.1%的误差,因此,大气加权平均温度的精度是实现高精度水汽反演和实时反演水汽总量的重要保证[3-4]。

国内外许多研究学者对加权平均温度开展了深入研究。Bevis首先提出了适合中纬度地区的Bevis经验公式,建立了地表温度Ts与加权平均温度Tm的线性关系[5];Ross 研究了全球53个无线电探空站23年的探空资料发现,随着测站地理位置与季节的变化,Tm发生变化[6];于胜杰[7]、李黎[8]等人研究了中国地区无线电探空站点资料,探究了加权平均温度Tm与纬度、海拔、地表温度Ts、水汽压和大气压的相关关系,并建立了实用性较强的回归模型;李建国应用了中尺度气象模式,建立了适合中国东部地区不同季节的关于Tm和Ts的线性回归方程[9];姚宜斌[10]、姚朝龙[11]等人提出无需气象资料的加权平均温度Tm;刘焱雄[12]、李剑锋[13]等人分别对不同地区加权平均温度本地化模型进行了研究。研究表明,加权平均温度时空特性明显,建立本地化模型对提高地基GPS反演水汽精度凸显重要。

本文根据青岛探空站2009-2011年3年的数据资料,建立适合青岛地区的大气加权平均温度模型,以达到精确、快速求得大气水汽含量的目的。

1 大气加权平均温度的计算原理

在GPS气象学中,可由对流层天顶湿延迟(ZWD)通过式(1)反演得到测站上空的可降水量(PWV),即:

PWV=Π·ZWD,

(1)

式中,Π为湿延迟与可降水量之间的转化参数,为无量纲系数,可表示为

(2)

式中:ρw为液态水的密度,值为1×103kg/m3;RV为水汽气体常数,值为461.495J·kg-1·k-1;k'2、k3为大气物理参数,经验值通常为22.13±2.20 K/hpa、(3.739±0.012)×105K/hpa[6];Tm为大气加权平均温度,单位：K,可以由测站上空水汽压和绝对温度沿天顶方向的积分函数求得,其数学表达式为

(3)

式中:e为测站天顶方向某高度的水汽压,单位：hpa;T为测站天顶方向某高度的绝对温度,单位：K;hs为测站大地高,单位：m.

目前,利用探空数据积分求得的加权平均温度是国内外学者公认的最精确的方法[14-15],利用探空数据计算加权平均温度的公式为

(4)

在常规探空资料中,水汽压ei并不是直接观测值,可以根据饱和水汽压es和露点温度t计算得到,公式为

(5)

ei=es×rh×100 ,

(6)

式中,rh为相对湿度。

2 青岛地区大气加权平均温度模型的建立

2.1 青岛地区Tm模型的建立

从怀俄明州立大学网站下载青岛探空站(120.33°E,36.06°N)2009-2011年的探空观测资料,由于探空气球每天仅探测两次(世界时00时和12时),因此可以获得世界时00时和12时的不同等压面的温度、露点温度、相对湿度等气象要素。按照不同的等压面,通过公式(4)计算3年的Tm值,并从探空资料中提取地表温度Ts.建立模型前,首先对Tm和Ts的时空变化特征进行分析,如图1所示为2009-2011年的Tm和Ts值散点图。

青岛探空站2009-2011年Tm的平均值为274.359K,Ts的平均值为283.425K,由图1可以看出,Tm和Ts四季变化明显,具有明显的年际单峰周期性变化,年内符合二次函数分布变化规律,1-8月份逐渐增大,夏季达到最高值,从9月份开始逐渐减少,冬季值最小。这是由于加权平均温度Tm的变化主要受太阳辐射和地球大气热辐射的影响,而太阳辐射和地球大气热辐射有周期性,除此之外,加权平均温度Tm还受区域天气系统的影响,冷平流使Tm下降,暖平流使Tm升高[16]。另外,加权平均温度普遍低于地面温度,且二者的整体升降趋势基本一致,升降幅度基本相同。

为进一步验证Tm与Ts的函数关系,以Ts为横坐标,Tm为纵坐标绘制出如图2所示的散点图。从图中可以看出,地面温度升高,加权平均温度随之升高,二者变化趋势一致,散点大致分布在一条直线附近,且在直线上下方波动,波动幅度大致相同,由此可见,加权平均温度与地面气温间存在较好的线性对应关系。由皮尔逊相关系数法,确定Tm与Ts的相关系数R为0.877 6,0.7≤|R|<1且为正,为强线性相关关系,因此,青岛地区Tm和Ts具有强线性相关性,且为正相关,运用回归分析方法,满足关系式:

Tmqd=aTs+b.

(7)

式(7)的误差方程为

(8)

利用最小二乘原则VTPV=min,解得a=0.97,b=-0.5575,即青岛地区的加权平均温度模型为

Tmqd=0.97Ts-0.5575 .

(9)

2.2 大气加权平均温度的精度分析

为了验证青岛地区本地化模型的精度,以青岛探空站数据资料直接计算的加权平均温度为真值Tm,以新建立青岛地区模型、Bevis模型和李建国模型计算的加权平均温度分别记为Tmqd、TmB、Tml,三种模型计算的2012年青岛探空站全年(样本数为730个)的加权平均温度值与真值的比较图如图3所示。

由图3(a)可以看出,新建立的本地化模型计算的Tmqd明显与真值拟合程度高,二者的协方差为89.864,无论在峰段(夏季)还是谷段(冬季),拟合度较高;由图3(b)和图3(c)可以看出,TmB和Tml在峰段(夏季)和谷段(冬季)处,偏离真值较大,协方差分别为66.704、75.041,可以发现,TmB较Tml偏离程度大,这是由水汽的区域性和时间特性决定的,Bevis模型是基于全球中纬度地区建立的,而李建国模型是基于中国东部地区建立的,局部区域建立的模型误差较小,适用性和可靠性更大。相对而言,新建立的青岛地区本地化模型为最佳模型,但由于夏季和冬季水汽变化较大,拟合程度略差。

如图4所示,分别为三种模型的计算值Tmqd、TmB和Tml与真值Tm的差值,由图可以看出,(Tmqd-Tm)与(Tml-Tm)上下波动范围相当,基本在±10 K内,而(TmB-Tm)略差,在±15K范围内;(Tmqd-Tm)基本在0 K上下浮动,全年波动幅度较为均匀,而(TmB-Tm)和(Tml-Tm)在夏季和冬季波动较大,大致呈上凹抛物线状,说明Bevis模型和李建国模型季节性明显。三种模型对比分析参数如表1所示。

表1 三种模型计算Tm对比分析参数

从表1可以看出,新建立的青岛地区加权平均温度模型的平均偏差为0.307 K,精度高于Bevis模型和李建国模型,标准差和均方根误差分别为3.359 K和3.384 K,具有较好的内符合精度,可以应用于青岛地区加权平均温度值的计算。

3 大气加权平均温度本地化模型在CORS反演水汽中的应用

确立大气加权平均温度的最终目的是为了地基GPS反演大气可降水量,因此,本文利用青岛地区CORS站反演大气可降水量,以验证CORS反演可降水汽及新建立的本地化加权平均温度模型的适用性和可靠性。

选用2012年8月7日～8月21日(年积日220-234)青岛地区均匀分布的CORS站点(LAIX、PIND、PJRS、RZRS、SZRS)、同期的青岛探空站数据及由中国气象数据共享网获取的各站点的地面温度值进行试验。为使网中有长于500 km的长基线以减少对流层延迟相关性[17],选用3个IGS站(BJFS、DAEJ和WUHN)与CORS站点联合解算。CORS站与探空站的位置如图5所示。

利用高精度数据处理软件GAMIT解算站点观测数据,其中,对流层模型选用Saastamoinen模型,映射函数选用VMF1,对流层参数估计间隔设置为12 h,并考虑了海洋潮、大气潮和天线相位偏差等改正,在met-文件中获取湿延迟ZWD和PWV.由中国气象数据共享网地面气温0.5 °×0.5°格点数据集内插出各站点的地表温度,根据新建立的本地化模型式(9)计算Tm,再由式(2)和式(1)计算PWV.

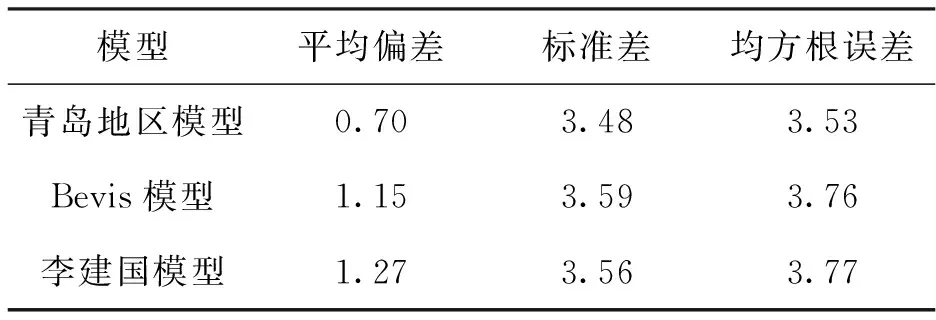
为便于分析,选取距离探空站最近的SZRS站,以探空站数据计算的PWV为真值[18],分别与由青岛地区模型、Bevis模型和李建国模型计算的PWV进行对比,如图6所示为根据三种模型计算的PWV时间序列图,表2示出了三种模型计算PWV的对比分析参数。

模型平均偏差标准差均方根误差 青岛地区模型0.703.483.53 Bevis模型1.153.593.76 李建国模型1.273.563.77

由图6和表2可以看出:

1) 由于新建立的青岛地区加权平均温度本地化模型、Bevis模型和李建国模型均由最小二乘拟合直线建立,因此由这三种模型计算的PWV变化趋势基本相同,而由于探空站与SZRS站相距19 km,高差为50 m,三者与探空资料计算的PWV存在一定的差值,但由于距离近,大气可降水量大致相同,可以用探空站计算的PWV值作为真值进行比较分析;

2) 相比Bevis模型和李建国模型,由本地化模型计算的PWV较逼近探空站计算的PWV,表2中本地化模型、Bevis模型和李建国模型与探空站计算的PWV的平均偏差分别为0.70 mm、1.15 mm和1.27 mm,同样可以看出本地化模型计算的PWV值较Bevis模型和李建国模型精度高;

3) 三种模型中,本地化模型的标准差和均方根误差最小,分别为3.48 mm和3.53 mm,说明本地化模型内符合精度较高,稳定性强,利用其计算PWV可靠性更高。

综上所述,相比Bevis模型和李建国模型,在CORS反演大气可降水量中,根据新建立的青岛地区加权平均温度本地化模型计算PWV具有精度高、稳定性强、可靠性高的特点,有利于水汽的监测和降水的预报。

4 结束语

本文利用青岛地区探空站资料建立了适合青岛地区的加权平均温度模型,将其应用在青岛CORS反演大气可降水量中,并与Bevis模型和李建国模型进行对比分析,得到以下结论:

1) 利用青岛地区探空数据资料建立的加权平均温度模型为:Tmqd=0.97Ts-0.5575,标准差为3.359 K,均方根误差为3.384 K,内外符合精度均在一定程度上优于Bevis模型和李建国模型;

2) 在CORS反演水汽中,采用本地化模型推算的PWV,与由探空站数据积分求得的PWV相比,标准差为3.48 mm,均方根误差为3.53 mm,两者在数值和变化趋势上接近,说明了青岛地区CORS站反演可降水量的适用性和可靠性,也说明了本地化加权平均温度模型的可用性。

需要说明的是,本文是以探空站数据资料为基础,建立青岛地区大气加权平均温度模型,探空数据的质量和分布密度对区域加权平均温度模型的建立影响很大,又由于青岛地区仅有一个探空站,并剔除了缺少露点温度和相对湿度的高层探空数据,从而导致探空资料不全,影响Tm和水汽的求取精度。虽然新建立的青岛地区的大气加权平均温度模型在一定程度上优于Bevis模型和李建国模型,但在精度和可靠性的提高程度上,尚需要做进一步研究。