改善单基站CORS RTK测量精度的自适应卡尔曼滤波算法

陈长坤,余学祥,石长伟,肖明,苏迪

(安徽理工大学 测绘学院,安徽 淮南 232001)

0 引 言

全球导航卫星系统(GNSS)在近年来得到了快速发展,已被广泛运用到各种工程变形、滑坡监测、大坝监测等动态变形测量系统[1-3],以及城市规划、市政建设和各种控制测量、精密工程测量中。随着无线通讯网络技术的快速发展和普及应用,以GNSS为基础的连续运行参考站(CORS)系统已在我国迅速得到推广和应用,成为各个城市空间数据的基础设施[4]。目前我国建立CORS系统的主要技术有虚拟参考站技术、主辅站技术以及单基准站模式。单基准站系统在原理上与普通参考站基本相同,并服务于一定作用半径内的用户。单基站CORS系统除了有CORS系统的各种功能外,还具有投入资金少、成本低、建设速度快、维护简单、系统结构简单等优点;但其作用距离短、作业精度随距离的增加而衰减等不足。

对于矿山开采沉陷地表移动变形监测,为了保证矿区的安全生产、加强矿区生态环境治理以及研究矿区开采时地表移动变形规律,就需要通过数据采集处理分析地表移动变形特征及规律[5-6]。常规的数据采集工作强度大,需要耗费大量的人力、物力、财力,所以地表移动监测点观测采用全站仪、数字式水准仪并结合单基站CORS RTK的测量模式[7-8]。采用常规测量与单基站CORS RTK测量相结合的方法可减少不必要的花销,减少劳动强度,节省项目经费和开支。

单基站CORS RTK技术具有采集数据快、架设简单与传统的实时动态(RTK)相比精度高等优势,但是其测量精度难以满足矿山开采沉陷监测的要求(根据《煤矿测量规程》,为了保证解算的开采沉陷关键参数的精度,要求相邻两期平面点位中误差≤±20 mm,最弱的高程中误差≤±10 mm,这就要求一次测量平面点位相对中误差≤±14 mm,最弱点高程中误差≤±7 mm,而单基站CORS RTK的平面位置精度约为±20 mm,高程精度约为±30 mm)[9-10].

为了提高单基站CORS RTK在矿山开采沉陷地表移动变形监测中的测量精度,本文采用基于方差分量估计原理的自适应卡尔曼滤波算法[11],利用实测数据,通过与滤波后的数据和水准测量成果相比较,获得滤波后的精度信息。

1 CORS RTK测量的卡尔曼滤波模型

1.1 卡尔曼滤波状态方程

设采用单基站CORS RTK测量的矿区监测网由n个监测点构成,可测量获得监测点的3维位置坐标(BJ-54坐标系下的高斯平面直角坐标和正常高),将t历元的3维位置坐标及其速率构成系统的状态向量。监测点i在历元t的位置坐标为ξi(t),瞬时速率为λi(t),瞬时加速率为Ωi(t),可将瞬时加速率看作一种随机干扰,则ξi(t)、λi(t)、Ωi(t)有以下微分关系:

(1)

记i点的状态向量为:

则该监测点的状态方程为

(2)

式中:0和E分别是三阶零矩阵和单位矩阵,对式(2)进行离散化处理可得卡尔曼滤波的状态方程为

(3)

式中,Δtk-1=tk-tk-1,tk-1和tk分别为第k-1历元和k历元的观测时刻,把n个监测点的状态方程组合可得全网的状态方程为

Xk=Φk,k-1Xk-1+Γk,k-1Ωk-1,

(4)

式(4)即为监测点的卡尔曼滤波状态方程。

1.2 卡尔曼滤波观测方程

通过测量可以得到第i个矿区监测点的3维空间位置坐标Li,k为观测值,某一监测点在第k历元的观测方程为

Li,k=ξi,k+Δti,kλi,k+Δi,k,

(5)

式中: Δti,k=ti,k-tk,ti,k为高差Lij的观测时刻;tk为监测点本次测量全部观测的中心时刻;ti,k在短时间内可忽略不计。

即:

Li,k=ξi,k+Δi,k,

(6)

可得全网的观测方程为

Lk=BkXk+Δk.

(7)

状态方程和观测方程两者共同组成监测站监测网的卡尔曼滤波模型:

(8)

式中：Φk,k-1为k-1到k历元的系统一步转移矩阵;Γk,k-1为系统噪声矩阵;Ωk-1为k-1历元的系统噪声；Bk为k历元系统的观测矩阵;Δk为k历元系统的观测噪声;Xk为k历元系统待估状态参数;Lk为k历元系统观测向量矩阵。Xk,Lk分别为矿区监测点的3维空间位置坐标向量和速度向量。

1.3 卡尔曼滤波算法

与式(8)对应的卡尔曼滤波递推为

X(k/k)=X(k/(k-1))+

Jk[Lk-BkX(k/(k-1))],

(9)

Dx(k/k)=(I-JkBk)Dx(k/(k-1)),

(10)

式中:I为单位矩阵;X(k/k)为状态滤波方程;DX(k/k)为滤波误差协方差阵；Lk-BkX(k/k-1)为预测残差;X(k/k-1)为一步预测值，

X(k/(k-1))=Φk/(k-1)X((k-1)/(k-1)),

(11)

Dx(k/(k-1))为预报误差协方差阵，

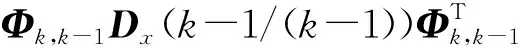
(12)

Jk为滤波增益矩阵，

(13)

式(9)和式(10)即是监测点三维位置的卡尔曼滤波递推计算公式,在确定初始状态后即可求得监测点三维位置的新状态参数滤波值。

2 基于方差分量估计原理的自适应卡尔曼滤波

2.1 自适应卡尔曼滤波算法

基于方差分量估计原理的自适应卡尔曼滤波是一种利用预报残差计算模型的动态噪声方差分量的自适应滤波算法。

将卡尔曼滤波方程写成高斯马尔科夫模型,将一步预测值Xk,k-1作为伪观测值,其协方差阵DXk,k-1与式(8)中观测方程联立可写成误差方程式:

V=AXk,k-1-L,

(14)

其中,误差方程的权阵为P;

(15)

上面有两种类型的观测值,即由一步预测值组成的伪观测值和实际观测值。下面根据验后估计原理,利用预报残差确定方差分量。

设预报残差表达式为

Vk=BkXk,k-1-Lk,

(16)

Lk,Xk,k-1的方差分别为

则预报残差为

(17)

通过平差,可得:

(18)

式中,m为观测值的个数。

(19)

(20)

(21)

由上述可知,利用预报残差在假设观测值方差先验已知时,用式(19)估计预测值的方差分量或者根据式(21)估计动态噪声分量,从而使动态噪声和观测噪声达到匹配状态,这可以有效克服滤波的不稳定性。

2.2 滤波初值的确定

从滤波递推方程可以看出来,要确定动态测量系统在任意时刻的状态(即3维空间位置及3维速率,不包含3维瞬时加速率,但可将其看作随机干扰),就必须要知道动态测量系统的初始状态,即要给该动态测量系统赋予初始值。

2.2.1 状态参数初值

对于单基站CORS RTK动态测量系统(主要获取监测点的3维空间位置序列)而言,状态参数是监测点的3维空间位置序列及其速率,而对动态测量系统来讲,滤波初值的选取尤为重要,选取不合适的初值则极大可能导致滤波发散。因此,三维空间位置坐标初值选取前3个历元的平均值,3维速率选取第2、3历元3维空间位置变化速率。

即

(22)

(23)

由式(22)和式(23)状态参数的初值为

(24)

2.2.2 状态参数初始方差阵

单基站CORS RTK动态测量系统的3维位置初始方差阵可取单位阵,即:

Dξ0=E.

(25)

由协方差传播定律,状态参数3维速率初值方差阵为

Dλ0=2Δt-2Dξ0,

(26)

式中,Δt为相邻历元间的采样间隔。

由式(25)和式(26)可得状态参数的初始协方差阵为:

(27)

2.2.3 动态噪声初始方差阵

将动态测量系统的瞬时加速率看作一种干扰,即瞬时加速率为状态的动态噪声,根据协方差传播定律动态噪声初始方差阵为:

DΩ0=4Δt-4Dξ0.

(28)

这样就可以获得单基站CORS RTK测量监测点的3维位置的初始状态。

3 算例分析

3.1 试验简介

为了验证本文提出的基于方差分量估计原理的自适应卡尔曼滤波算法求解数学模型的正确性。在淮南矿区朱集东矿1222(1)工作面上进行试验,试验水准监测网如图1所示。该采煤工作面监测站由一条走向观测线、半条倾向观测线以及庙东北村、前圩村若干个监测站构成,倾向观测线(控制点CS01-CS03,监测点MS01-MS39)和走向观测线(控制点CL01-CL06,监测点ML01-ML90),走向观测线及观测站如图2所示,共布设9个控制点和129个监测点,本次试验只选取走向观测线监测站的数据进行分析。

为了及时掌握工作面开采对村庄的破坏情况以及该工作面上地表移动变形规律,试验采用传统水准测量(1台Lecia Sprinter 250数字式电子水准仪)和单基站CORS RTK同时进行外业数据采集。单基站CORS RTK测量采样率设置为1 s,连续观测1 min(即每个监测点观测60次)。CORS RTK测量数据内业处理,分别采用常规的数据处理方法和本文提出的基于方差分量估计的自适应滤波处理方法。

水准测量按四等水准的要求,采用最小二乘约束网平差的方法进行平差计算。监测点的高程统计信息如表1所示,平差后高程中误差最高可达0.7 mm,最低精度2.3 mm,平均精度1.9 mm,每千米观测高差全中误差为±3.2 mm.因此水准测量的成果可作为单基站CORS RTK高程测量成果的检核信息。

表1 监测点高程中误差统计信息

3.2 数值结果与分析

表2和表3示出本次试验中CORS RTK测量值和自适应卡尔曼滤波值的平面位置和高程精度统计信息,取所有历元的平面位置坐标中误差和高程中误差进行精度评定。

设某一时段i观测了n个历元,则其平均值的平面坐标中误差和高程中误差为

(29)

对于滤波值,设某一时段i观测了n个历元,取各个历元滤波后的平面位置坐标和高程的平均值作为该历元的最终成果,即:

(30)

则平均中误差为

(31)

有:

(32)

表2 CORS RTK平面精度统计信息

表3 CORS RTK高程精度统计信息

从表2和表3中可以看出,CORS RTK测量值其平面位置最低精度为1.85 cm,最高精度为0.23 cm,平均精度为0.95 cm;高程最低精度为3.92 m,最高精度为1.24 cm,平均精度为2.13 cm.平面精度满足开采沉陷测量精度要求,但高程却达不到相应的精度要求。滤波后的平面位置最低精度为0.99 cm,最高精度为0.12 cm,平均精度0.54 cm,平面位置平均精度提升了2倍左右普;高程最低精度为1.54 cm,最高精度0.32 cm.平均精度为0.65 cm,高程精度平均提高了3倍左右。

表4 高程测量差值统计信息

表4示出了1222(1)工作面走向观测线监测点与水准测量的高程测量值差值统计信息。对于常规的单基站CORS RTK测量而言,其转换后的正常高与水准测量差异大,差值在2 cm以内监测点的比率为50%,差值大于3 cm的比率为24.4%,差值中误差为1.09 cm,难以满足开采沉陷对高程测量的要求。

滤波后差值在2 cm以内监测点的比率增加到80%,增加了30%;差值大于3 cm的比率减小到6.7%,减少了近20%。滤波后的CORS RTK正常高与水准测量成果比较,差值减小,最大差值3.12 cm,最小仅0.32 cm,平均差值为0.65 cm,差值中误差0.67 cm,满足开采沉陷监测对高程测量的精度要求(根据《煤矿测量规程》,为了保证解算的开采沉陷的关键参数的精度,要求相邻两期平面点位中误差≤±20 mm,最弱的高程中误差≤±10 mm,这就要求一次测量平面点位相对中误差≤±14 mm,最弱点高程中误差≤±7 mm)。

从以上分析可以看出在单基站CORS RTK测量监测站的3维位置坐标中,自适应卡尔曼滤波值相较实测值精度得到大幅提高,其更能真实体现地表移动变形动态数据的实时性;使滤波过后的每个历元的测量成果更为稳定和可靠,这为更进一步获得稳定的移动变形量提供了坚实基础。

4 结束语

在矿山开采沉陷地表移动变形监测中,为了改善并提高单基站CORS RTK测量的精度(平面位置和高程,特别是高程),结合开采沉陷的特点,建立基于方差分量估计原理的自适应卡尔曼滤波算法,对单基站CORS RTK测量得到监测点的位置信息进行滤波处理;对其测量成果采用该滤波算法后,其平面位置和高程精度得到大幅度提升,使滤波后的成果更为稳定可靠。

滤波后其平面精度平均提高2倍左右,其完全满足矿山开采沉陷对平面位置的精度要求,高程精度平均提高3倍左右。与水准测量成果比较可得滤波后差值与滤波前相比得到了大幅度提高,平均差值提高了约2倍多,基本满足矿山开采沉陷对高程的要求。

但是由于影响单基站CORS RTK测量精度的因素还有很多,本文没有全部说明,只是从算法角度去改善其测量精度。RTK本身硬件导致的误差、天线相位中心偏差以及测区的观测条件等因素,也是要考虑到的问题。