平面P波在半圆形凹陷场地产生的动应力路径

刘廷峻 汪 刚

(1.中国地震局工程力学研究所，黑龙江 哈尔滨 150080; 2.中国地震局地震工程与工程振动重点实验室，黑龙江 哈尔滨 150080)

近几十年来，估计地表局部不规则地形对地震地面运动影响的研究工作一直是地震学、地震工程学中令人关注的课题之一。地表局部不规则地形对地震地面运动影响作为宏观现象，其本质是弹性波的散射与动应力集中。弹性波的散射与动应力集中问题[1]是近几十年提出的课题，它在理论上，特别是工程应用上有重要的意义。在研究土体的动力学特性时，Ishihara等[2]在计算波浪对海床的作用时提出了动应力路径的概念，以土体单元为研究对象，选取竖向应力与水平向应力之差的1/2作为横坐标，选取剪应力作为纵坐标，绘制动应力路径。动应力路径的概念在研究车辆动载下地基的响应和飞机荷载下跑道道基的响应时得到了广泛的应用，魏星等[3]在研究移动交通荷载下公路软土地基的沉降计算时考虑了土体的动应力路径，张凡[4]在研究飞机单轮荷载作用下山区机场跑道动力响应时考虑了土体的动应力路径。本文基于波动理论，推导了平面P波斜入射时半圆形凹陷场地不同位置处土体应力的计算公式，分析了平面P波入射时表面土体的位移幅值和内部土体的动应力路径，并比较了半圆形凹陷场地与半无限场地之间的差异。

1 采用模型与方法

1.1 采用模型

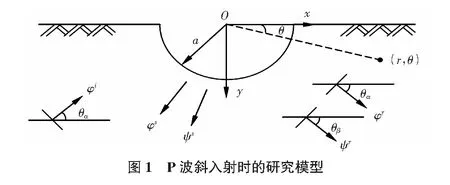
根据弹性波动力学基本理论[5]，本文对研究模型进行了一定的简化，如图1所示。假定场地为包含半圆形凹陷的平面半无限体，半圆形凹陷的圆心在O点，半径为a，土体为线弹性，波在传播过程中没有能量的衰减。

1.2 平面P波入射下的土体应力状态

1.2.1自由场

设入射P波势函数为:

φi=expiα(xcosθα-ysinθα)

(1)

其中，上标i表示入射波；波数α=ω/vp；ω为圆频率；vp为P波波速；θα为入射波和法线的夹角。

入射P波时存在波型转换现象，产生反射P波和反射SV波。自由场的P波和SV波的势函数为：

φff=expiα(xcosθα-ysinθα)+K1expiα(xcosθα+ysinθα)

(2)

ψff=K2expiβ(xcosθβ+ysinθβ)

(3)

其中，K1和K2均为反射系数。

自由场的P波和SV波势函数可展开为柱面波函数：

(4)

(5)

其中，an,bn,cn,dn均为已知系数。

1.2.2散射场

散射波的势函数为：

(6)

(7)

其中，上标s表示散射波；An,Bn,Cn,Dn均为未知系数。

1.2.3边界条件

平面和凹陷处均为自由边界，故满足：

σθ|θ=0,π=0

(8)

τrθ|θ=0,π=0

(9)

0≤θ≤π，σr|r=a=0

(10)

0≤θ≤π，τrθ|r=a=0

(11)

1.2.4未知系数的求解

极坐标下应力—势函数的关系为:

(12)

(13)

(14)

Lee[6]提出了一种算法，如式(15)，式(16)所示，在半空间中将正弦函数用余弦函数表示，从而将未知系数减少至An和Cn。

(15)

式中:

(16)

故散射波导致的应力可以表示为:

(17)

(18)

(19)

将式(17)～式(19)代入式(8)，式(9)可直接满足。将式(17)～式(19)代入式(10),式(11)可得:

(20)

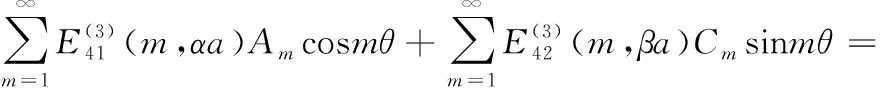
(21)

σx=σrcos2θ+σθsin2θ-2τrθsinθcosθ

(22)

σy=σrsin2θ+σθcos2θ+2τrθsinθcosθ

(23)

τxy=(σr-σθ)sinθcosθ+τrθ(cos2θ-sin2θ)

(24)

到此为止，平面P波入射下，由式(22)～式(24)可以确定土体中任意一点的应力状态。

2 土体表面位移幅值分析

极坐标下位移—势函数的关系为:

(25)

(26)

再使用式(27),式(28)可以得到位移分量在直角坐标系中的表达式：

ux=urcosθ-uθsinθ

(27)

uy=ursinθ+uθcosθ

(28)

入射平面P波时，选取土体表面的位移幅值进行分析。土体参数为：密度ρ=1 800 kg/m3，剪切波速vs=2 000 m/s，泊松比υ=0.25。凹陷的半径为1 000 m。入射波频率2 Hz，入射波成60°入射。

如图2所示，由于凹陷场地的影响，地表位移幅值发生了较大的变化，放大效应最大的地方是凹陷的边缘，面对入射波一侧比背对入射波一侧放大效应更加明显；半圆形凹陷内部的位移幅值比两侧水平面的位移幅值规律更加复杂，并且受位置的影响更大。

3 土体动应力路径分析

入射平面P波时，选取不同位置的土体进行分析和对比，选取(σy-σx)/2作为横坐标，τxy作为纵坐标，绘制动应力路径。土体参数和入射波和上一节相同。

选取半圆形凹陷场地和半无限场地中直角坐标为(-1 800,3),(-1 800,7),(-1 800,10),(-1 800,15),(1 800,3),(1 800,7),(1 800,10),(1 800,15),(1 200,3),(1 200,7),(1 200,10),(1 200,15)的点绘制动应力路径。

如图3～图5所示，半圆形凹陷场地和半无限场地的相同点是动应力路径都是椭圆。不同点是，相同位置处，半圆形凹陷场地面对入射波的椭圆(如图3所示)的高度和宽度都大于半无限场地，说明面对入射波一侧的土体正应力差和剪应力都要大于半无限场地；半圆形凹陷场地背对入射波一侧，有的椭圆(如图4所示)高度和宽度大于半无限场地，有的椭圆(如图5所示)高度和宽度小于半无限场地，说明面对入射波一侧的土体正应力差和剪应力都要小于半无限场地。

在地基、边坡的地震稳定性分析中，需要考虑到土体在往返荷载作用下的强度，对土体不同位置处动应力路径的研究可以应用于寻找场地中地震稳定性最危险的位置。

4 结语

本文基于波动理论，推导了地震波斜入射时半圆形凹陷场地不同位置处土体应力的计算公式，分析了平面P波入射时表面土体的位移幅值和内部土体的动应力路径，并比较了半圆形凹陷场地与半无限场地之间的差异，在本文的假设条件下，得到以下结论：

1)入射平面P波时，凹陷场地导致的放大效应最大的地方是凹陷的边缘。

2)入射平面P波时，半圆形凹陷场地和半无限场地土体的动应力路径都是椭圆。

3)受凹陷和位置等因素影响，椭圆的高度、宽度、倾斜程度发生变化。